堆排序中首先需要做的就是建堆,广为人知的是建堆复杂度才O(n),它的证明过程涉及到高等数学中的级数或者概率论,不过证明整体来讲是比较易懂的。
堆排过程
代码如下
void print(vector<int> &arr)
{
for(auto n: arr) printf("%d ", n);
cout<<endl;
}
// 以arr[n]为根的子树,将arr[n]向下调整至合适位置
void Heapify(vector<int> &arr, int size, int n)
{
int L = n*2+1, R = L+1;
if(L>=size) return ;//无孩
int big = arr[L]; // 取两孩之大者
if(R<size) big = max(big, arr[R]);
if(arr[n]>=big) return ; //无需调整
int c = L; // 欲与父交换位置的孩子
if(big!=arr[L]) c = R;
swap(arr[n], arr[c]);
Heapify(arr, size, c);
}
// 小根堆
void BuildHeap(vector<int> &arr)
{
int last = (arr.size()-1)/2;
for(int i=last; i>=0; i--) {
Heapify(arr, arr.size(), i);
}
}
// 顺便排序
void Sort(vector<int> &arr)
{
int size = arr.size();
for(int i=size-1; i>0; i--) {
swap(arr[0], arr[i]);
Heapify(arr, i, 0); //调整一下arr[0]
}
}
int main()
{
vector<int> vect{9, 10, 6, 3, 1, 6, 2, 8, 4};
print(vect); //排序前
BuildHeap(vect); //建堆
Sort(vect); //排序
print(vect); //排序后
return 0;
}
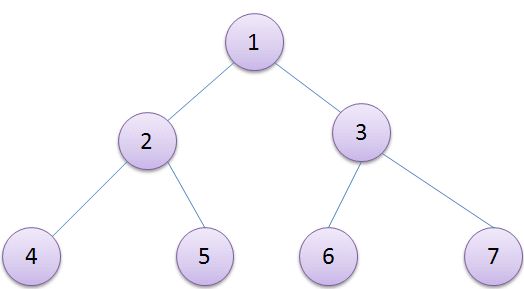
建堆的过程就是从最后一个分支结点开始逐层向上遍历,将结点向下调整至合适的位置,以不至于破坏原来的堆。比如上图,遍历的结点编号依次为3 2 1,首先调整以3为根的子树成堆,其次是以2为根的子树成堆,最后是以1为根的子树成堆。至此建堆完成,复杂度O(n)。
注意:建堆不能写成如下这样,这样的建堆算法复杂度是O(nlogn),虽然不会影响堆排序的复杂度O(nlogn),但是实现其他算法时就很不利了。
// 将arr[n]向上调整至合适位置
void AdjustHeap(vector<int> &arr, int n)
{
if(n<=0) return ;
if(arr[(n-1)/2] > arr[n]) { //与父结点比较
swap(arr[(n-1)/2], arr[n]);
AdjustHeap(arr, (n-1)/2); //递归调整
}
}
// 小根堆
void BuildHeap(vector<int> &arr)
{
for(int i=1; i<arr.size(); i++) {
AdjustHeap(arr, i);
}
}
复杂度计算
从直观上看,Heapify()的递归深度最多为({log_n}),故它的复杂度上限为O(logn)。而BuildHeap()中的循环为({ frac{n}{2} })次,故它的复杂度为O(nlogn),但这不是它的实际复杂度,而是一个估算的上界,它很可能永远达不到这个上界。为了方便计算,考虑结点数量为n,高度为h的满二叉树,因此({2^h-1 = n}),即({h = log_2{(n+1)}})。
| 第几层 | 最多调整次数 | 层调整次数累计 |
|---|---|---|
| ({h}) | (0) | ({2^{h-1}*0}) |
| ({h-1}) | (1) | ({2^{h-2}*1}) |
| ({h-2}) | (2) | ({2^{h-3}*2}) |
| (vdots) | (vdots) | (vdots) |
| (3) | ({ h-3 }) | ({2^{2}*(h-3)}) |
| (2) | ({ h-2 }) | ({2^{1}*(h-2)}) |
| (1) | ({ h-1 }) | ({2^{0}*(h-1)}) |
将最右边一列累加起来就是建堆的调整次数,则建堆的调整次数({S(n)})为
[{S(n) = 1*2^{h-2}+2*2^{h-3}+}cdots {+(h-2)*2^1 +(h-1)*2^0}
]
[{=2^{h-1} * ( frac{1}{2^{1}} +frac{2}{2^{2}} +frac{3}{2^{3}} +}cdots {+frac{h-2}{2^{h-2}} +frac{h-1}{2^{h-1}} )} ag{1}
]
则
[{frac{1}{2} S(n) = 2^{h-1} *(frac{1}{2^2} + frac{2}{2^3} + frac{3}{2^4} + }cdots{+frac{h-2}{2^{h-1}} +frac{h-1}{2^h})} ag{2}
]
将(1)式减去(2)式得
[{S(n)-frac{1}{2}S(n) = 2^{h-1} * (frac{1}{2^1} + frac{1}{2^2} + frac{1}{2^3} + }cdots{+frac{1}{2^{h-2}} + frac{1}{2^{h-1}} -frac{h-1}{2^h} )}
]
[{ = 2^{h-1} * (frac{1}{1-frac{1}{2}}-1-frac{h-1}{2^h} ) } ag{3}
]
[{ =2^{h-1} * ( 1 - frac{h-1}{2^h})}
]
[{ =2^{h-1}}
]
又因 ({ n = 2^h-1 }),故有
[{S(n) = 2^h = frac{n+1}{2}}
]
注意:上面列式均是当n趋于无穷大时的计算,且(3)式是由级数的直接变换所得。其他的证明思路还有用概率的,就不写了。
写公式写到头皮发麻,写错n次了,如果错漏请不吝指正,感谢!