在一块电路板的上、下两端分别有n个接线柱。根据电路设计,要求用导线将上端接线柱与下端接线柱相连
,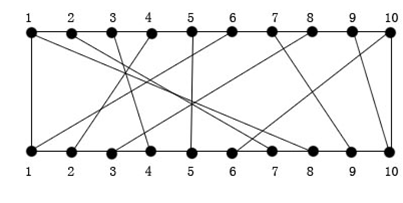
如上图所示,每个节点有且只连有一条线。
在制作电路板时,要求将这n条连线分布到若干绝缘层上。在同一层上的连线不相交。
这个问题是要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线(不相交)。
为了解决这个问题,我们可以 将问题简化为这样:
设定上接线柱为1,2,3,....,n。
下接线柱是【 1,2,3,....,n】的一个排列 设为f(i),i的值就是上接线柱的数字,
如上图就是这样的模型:
i 1 2 3 4 5 6 7 8 9 10
f(i) 8,7,4,2,5,1,9,3,10,6
它们一一对应。
我们还必须得到这样一个结论:
对于上接线柱i1<i2<i3<...<ik来说。它们与下接线柱f(i)的连线之间互不相交的充要条件是:
f(i1)<f(i2)<...<f(ik)。这个结论是很显然成立的。
因为对于i1<i2如果f(i1)>f(i2)则它们一定相交(画出图像来看看)
因此,我可以将这个电路布线问题,转化为这样的问题:
已知有一个{1,2,3,...,n}的排列,将其拆分为k个子排列,并且每个子排列都是严格递增的,求子排列的最大元素个数。
例如:排列 8,7,4,2,5,1,9,3,10,6可以拆分成五个子排列{4,5,9,10}{8}{7}{2,3,6}{1} 。
它最大的元素个数是4。
排列 1,2,3,4,5,6,7,8,9,10它是递增的,所以无需拆分,最大元素个数是10。
算法实现:
对于排列8,7,4,2,5,1,9,3,10,6。
先将记录第一个值8,依次向后扫描至大于8的元素。如果发现8的元素,例如9,则我可以产生一个子排列{8,9}(实际上只需要更改元素数量和最大值即可),继续扫描。
产生子排列{8,9,10}。扫描完毕后姑且认为子排列最大元素是3个。
第二次以7向后扫描,只要扫描到比它大的,就将产生一个子排列,继续向后扫描,扫描结束后,得到排列是{7,9,10}。个数是3,与之前的比较。
第三次以4开始扫描,。。。依次下去至扫描结束。
使用递归算法代码简单,算法复杂度为O(N*N)
#include <iostream> using namespace std; #define N 10 int sub[N] = { 2, 7, 3, 4, 5, 6, 9, 8, 10, 1 }; int function(int MaxElem,int e=0,int counts=1) { if (e==N-1) { //递归的出口 if (sub[e] > MaxElem) counts++; return counts; } else { if (sub[e]>MaxElem) { MaxElem = sub[e]; counts++; } return function(MaxElem,e+1,counts); } } int main() { int max = 0,t; for (int i = 0; i < N; i++) { if ((t = function(sub[i]))>max) max = t; } cout << max << endl; return 0; }