今天是廖俊豪老师的讲授~
T1

第一次想出正解
30 pts:
k <= 10,枚举如何把数放到矩阵中,O ( k ! );
100 pts:
对于矩阵的每一列,我们二分最小差异值,然后贪心去判断是否可行;
贪心策略:从前往后找,如果有从某个数开始往后连续的 m 个数,这 m 个数的最大值 - 最小值 < k,那么就把这 m 个数放到同一行,最后判断是否能够凑出 n 行;
std 标程:
#include<bits/stdc++.h> using namespace std; const int maxn = 1e5 + 7; int n, m, k, v[maxn]; int judge(int d) { int tmp = 0; for (int i=1; i+m-1<=k; ++i) { if (v[i+m-1] - v[i] <=d) ++tmp, i += m - 1; } if (tmp >= n) return 1; return 0; } int main() { freopen("a.in", "r", stdin); freopen("a.out", "w", stdout); scanf("%d%d%d", &k, &n, &m); for (int i=1; i<=k; ++i) scanf("%d", &v[i]); sort(v + 1, v + k + 1); int left = 0, right = 1e9; while (left < right) { int mid = (left + right) / 2; if (judge(mid)) right = mid; else left = mid + 1; } printf("%d ", left); return 0; }
我的拙码:
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } const int N=5e5; int n,k,m,l,r=-1e9,ans; int val[N]; bool check(int x) //每行最大值减去最小值都要小于等于x { int tot=0; //我们能匹配到tot行了 for(int i=1;i+m-1<=k;i++) { if(val[i+m-1]-val[i]<=x) //中间的点都可以选在同一行,那么两头的分别就是最大最小值 { tot++; i=i+m-1; } if(tot==n) return 1; } if(tot<n) return 0; else return 1; } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); k=read();n=read();m=read(); for(int i=1;i<=k;i++) { val[i]=read(); r=max(r,val[i]); } sort(val+1,val+1+k); l=0; while(l<r) { int mid=(l+r)>>1; if(check(mid)) r=mid,ans=mid; else l=mid+1; } printf("%d",ans); return 0; }
T2

30 pts:
枚举分割点的位置,然后一顿瞎搞,O ( n ! ) ;
60 pts:
我们完全可以用 dp 来做(然后我就写炸了。。。)
我们先预处理出每一段的或和, 用 sum [ i ][ j ] 存起来;
f [ i ][ j ] 表示考虑了前 i 个数,分成 j 段的最大和 。
考虑转移:
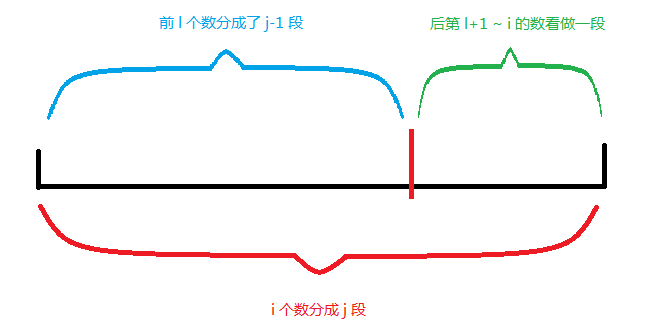
f [ i ][ j ] = max ( f [ i ][ j ] , f [ l ][ j-1 ] + sum [ l+1 ][ i ];

100 pts:
我们考虑去优化 dp;
我们发现两个数组具有单调性:
f [ l ][ j-1 ] 随着 l 的增加递增;
sum [ l+1 ][ i ] 随着 l 的增加而递减;
对于固定的 i,sum [ k+1 ][ j ] 的取值最多只有 32 种,而且 f 数组的值单调递增。预处理出转移点即可。
时间复杂度 O ( n * k * log C ),C 为 v [ i ] 的上界
100+ pts:
时间复杂度 O ( n k ) ? O ( n log C ) ? 欢迎补充
B_extended:将最大值改为最小值,怎么做?

T3



令 n = 2k , C ( x , y ) 为在 x 个物品中选择 y 个不同的物品的方案数,树的最底层为 0 。
30 pts:
k <= 3,也就是说 n <=8 ,我们可以直接枚举 n 的全排列,把所有的情况加起来!
60 pts:
k <= 10,n <= 1024;
求出所有情况的魔法值;
考虑:两个点 x 和点 y 在第 d 层对答案的贡献;
算清楚 x 和 y 在第 d 层相遇了多少次:Σ(v [ x ] * v [ y ] * times [ x ][ y ][ d ]);
不妨考虑 2d - 1 个编号小于 y 的;
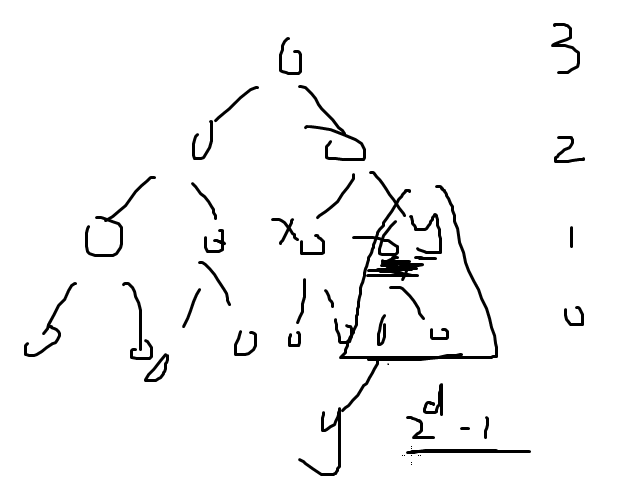


这才 60 pts 就已经晕了,那么接下来讲 100pts 的:
更改求和顺序,改为 2 * 2k! * 2k! * ( n - 2k+1 ) ! * C ( y-1 , 2k - 1 ) * v [ y ] * C ( x - 1 - 2k , 2^k-1) * v [ x ] ,枚举 k 和 y,我们知道 x >= max ( 2k+1 , y+1 ),先对 C ( x - 1 - 2k , 2k - 1 ) * v [ x ] 求后缀和即可。时间复杂度 O ( n * k );
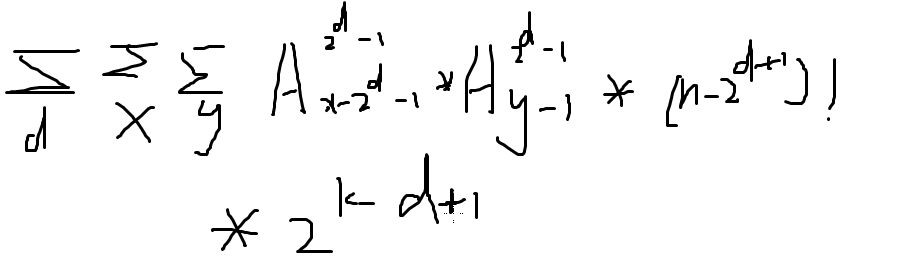
我们可以预处理:
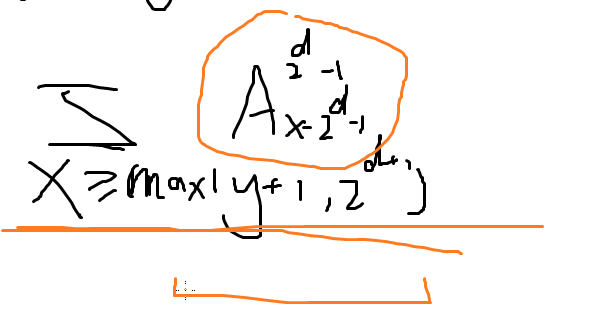
数论




POJ 3735 Training little cats
有 n 只猫,有三种操作:
1、让第 i 只猫花生数 +1;
2、吃光第 i 只猫拥有的花生;
3、交换两只猫拥有的花生;
给出一个长度为 k 的操作序列,求将这个操作序列循环 m 次之后,每只猫拥有的花生数量;
![]()
题解:
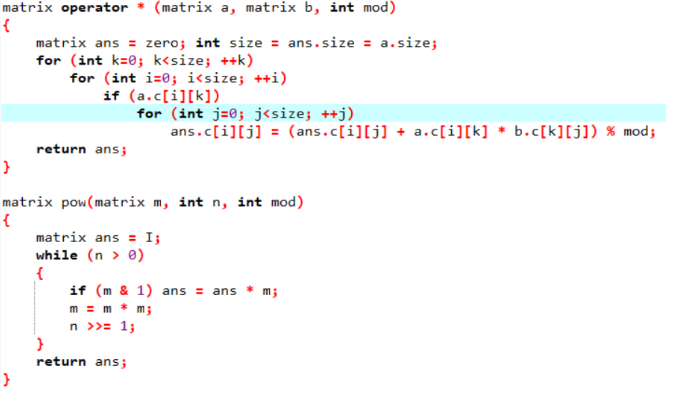
在线性代数中,矩阵乘法可以表示向量的变换;
将 n 只猫拥有的花生数量看成一个列向量;
操作1:向量的平移变换;
操作2:向量的投影变换;
操作3:向量的旋转变换;
找出每种操作对应的矩阵,依次做乘法即可;

考虑到 n 的范围太大, O ( n ) 的算法不大行,我们要想 log n 的算法;
自然想到了快速幂,我们用矩阵快速幂试试:

考虑到 k 是在不断变化的,但是最多就 18 种,所以我们做 18 次矩阵快速幂就好了,总时间复杂度 O(18 * 33 * log n);
欧几里得算法:
给定数 a 和数 b,求两个数的最大公约数;
欧几里得算法(辗转相除法)
gcd(a , b)= gcd(b , a%b);
时间复杂度 O(log C);
扩展欧几里得的算法
求 ax + by = gcd(a,b)的一组整数解;
或者判断 ax + by = k 是否有解;


P1516 青蛙的约会

题解:
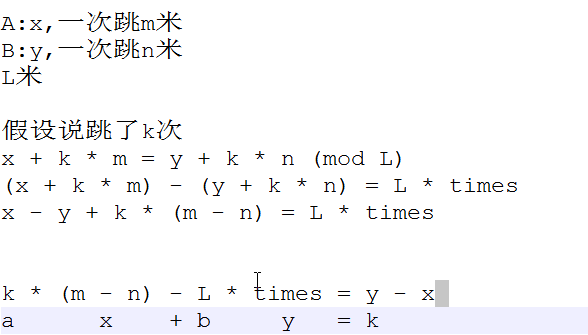
最小公倍数
判断素数
给定一个数 n,判断 n 是否为素数;

筛素数
给定一个n,判断 1—n 这 n 个数哪些是素数;
N ≤ 106
用朴素的方法一个一个判断不可行;
只要一个数是某个质因数的 k 倍(k > 1),那么这个数就是合数;
数组 flag 表示每个数是不是素数;
如果一个数是素数,则这个数的倍数都是合数;
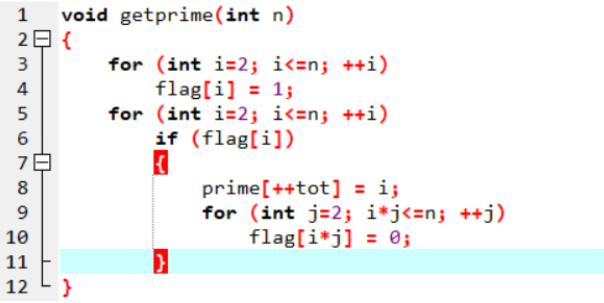
算法复杂度估计:O ( n ) – O ( n log n );
实际算法复杂度:O ( n loglog n );
线性筛素数
普通筛素数的方法里,一个合数有可能会被重复筛去多次,因此效率不高;
改进思想:尽量少重复筛素数;
先贴上代码:
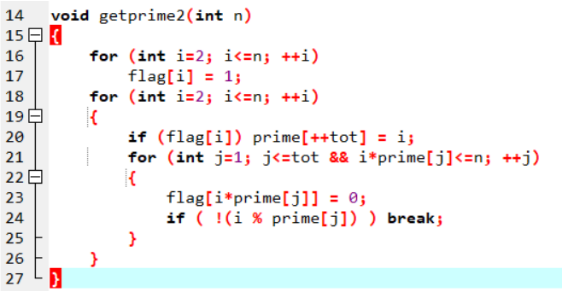
为什么时间复杂度是 O ( n )?
需要证明的东西:
1、我们不会重复删掉一个合数;
2、1~n 的合数都会被我们找出来;

对于一个合数,肯定能表示成:一个数 * 一个小素数 的形式;
因此所有的素数都能被我们筛出来;
算法正确性可以证明;

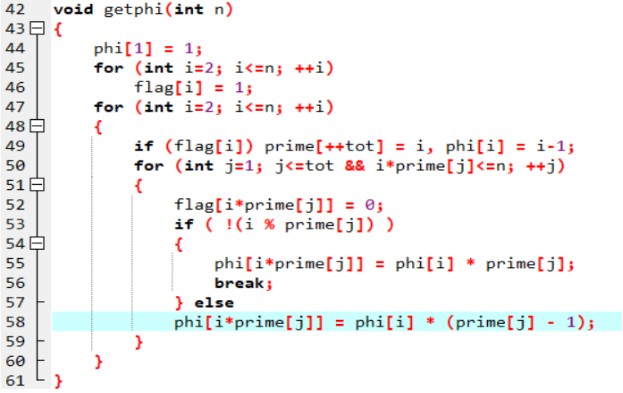
欧拉函数

欧拉函数:给定数 n,求小于等于 n 中与 n 互素的数的个数;
等价于求 φ ( n );
等价于求 n 的质因数分解;
O ( √n );
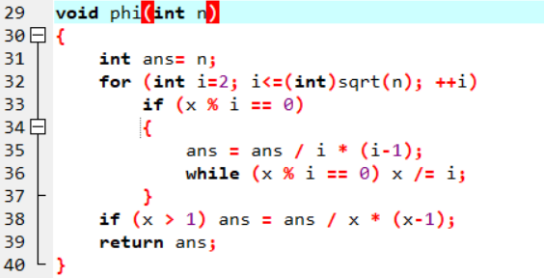
线性求欧拉函数
给定一个数 n,要求 1-n 中所有数的欧拉函数;
利用欧拉函数的积性:
性质5:若 a、b 互质,则 φ ( a * b ) = φ ( a ) * φ ( b );
a % b == 0 , φ ( a * b ) =φ ( a ) * b;
费马小定理&欧拉定理
逆元
求逆元
线性求逆元
给定素数 p,求 1~p-1 中每个数在模 p 意义下的的逆元;

BZOJ 2705 [SDOI2012] Longge的问题
题目描述:Longge 的数学成绩非常好,并且他非常乐于挑战高难度的数学问题。现在问题来了:给定一个整数 N,你需要求出 ∑ gcd ( i , N ) ( 1 <= i <= N )。
对于 60% 的数据,0< N <= 216 。
对于 100% 的数据,0 < N <= 232 。
题解:
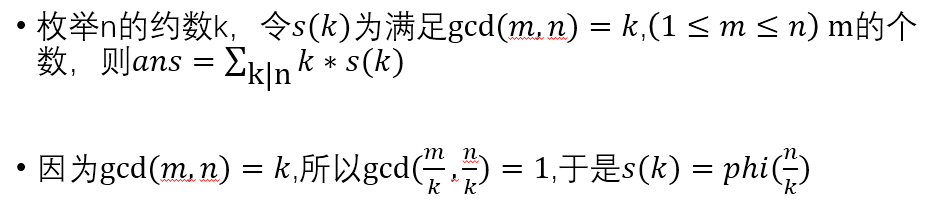
组合数

杨辉三角
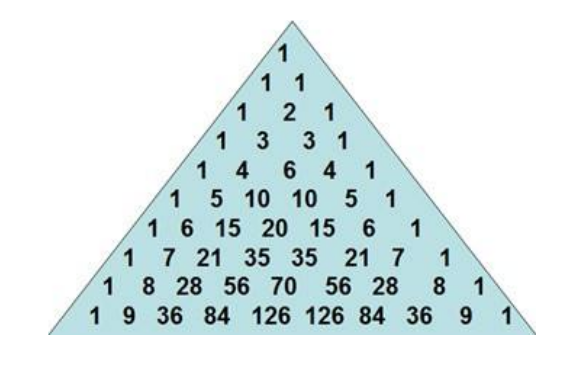
二项式定理
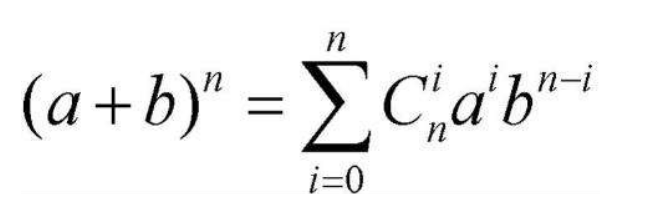
同余

组合数取模:问题一
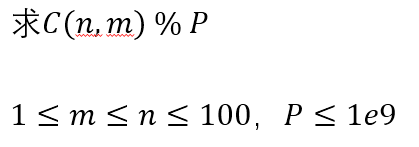
题解:
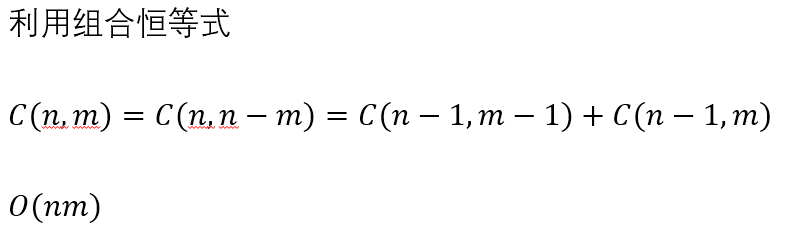
问题二
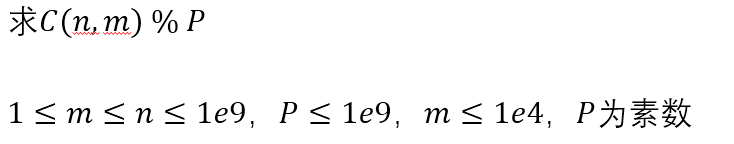
题解:

问题三
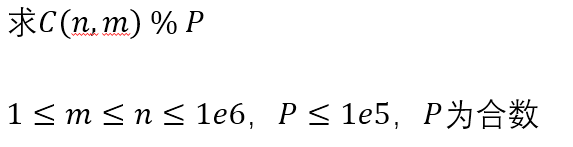
题解:
P 为合数,对于 0~(p-1),不是每个数都有 ( mod p ) 意义下的逆元;
但是 n , m , p 都不大,考虑组合数的计算式的变形:
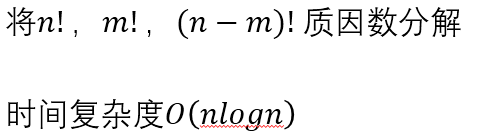
问题四
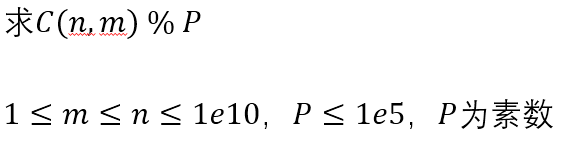
Lucas定理
![]()



问题五

题解:
Lucas 定理 + 中国剩余定理;
用 Lucas 定理后得到 k 个同余方程;
怎样合并这 k 个同余方程是我们要解决的问题;
中国剩余定理

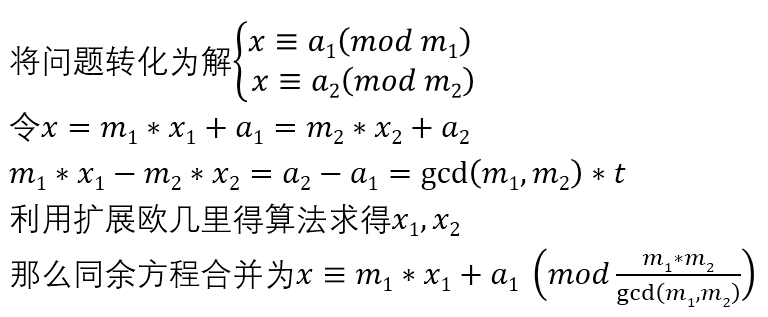

问题六

题解:
扩展卢卡斯定理;
[ZJOI2010]排列计数

题解:
对于一个 n 个元素的二叉堆,其左右儿子为根的对,大小是确定的;
那么设左儿子的对大小为 l,右儿子的对的大小为 r,r = n - l - 1;
为什么是 n - l - 1 呢?因为根也占一个元素;
设 f [ i ] 表示 i 个元素组成的二叉堆的方案数;
f [ n ] = C ( n-1 , l ) * f [ l ] * f [ r ] % p;
若 p 很大,直接做;
若 p 很小,1……p-1 的数是有逆元的;
Lucas 定理,注意 p 必须是素数才能用;
高斯消元
解方程组;
思想:利用加减消元法解方程;
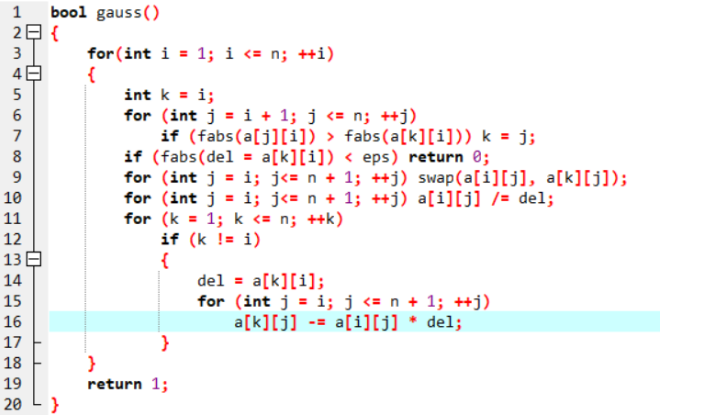
[HNOI2013]游走

题解:
期望走过的次数越大的边,编号越小 ==> 要求总分的期望最小;
每个点的期望经过次数 ==> 求每条边的期望经过次数;
一条边 编号为 k,端点为(x,y)
p [ x ] 表示第 x 个点的期望经过次数;
du [ x ] 表示与 x 相连的点数;
那么低 k 条边的期望经过次数就是 p [ x ] * 1 / du [ x ] + p [ y ] * 1 / du [ y ];
假设 x 号店与 t1 , t2 , t3 ,..... tk 相连;
p [ 1 ] = p [ t1 ] / du [ t1 ] + p [ t2 ] / du [ t2 ] + ...... + p [ tk ] / du [ tk ] + 1;
p [ x ] = p [ t1 ] / du [ t1 ] + p [ t2 ] / du [ t2 ] + ...... + p [ tk ] / du [ tk ] ;
有了 n 个方程,n 个未知数,高斯消元;
大步小步算法
![]()


课后作业:Bzoj2242:[SDOI2011]计算器

老师的手稿证明过程:


NOIp 会涉及到的数学相关知识:
1. 快速幂;
2. 矩阵乘法;
3. GCD / exGCD;
4. 筛素数 / 素数判断;
5. 欧拉函数 / 质因数分解;
6. 逆元;
7. 组合数问题 / 卢卡斯定理 ;
8. 中国剩余定理;
9. 高斯消元;


