原题链接 https://www.luogu.org/problem/P1850


这是一道期望 dp 的题目,其中还有不少坑,AC 的道路上充满坎坷啊~
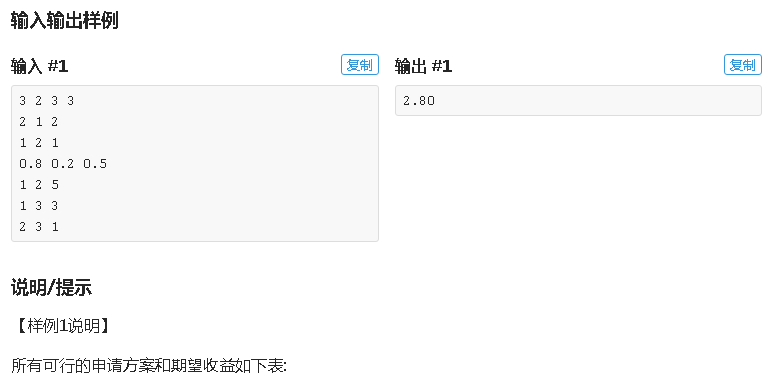
简化题意
有 v 个点 e 条边,需要在其中某些点里上课,并有几率换到另外别的点上去,但是只要 m 次机会可以换(只是可以,不一定成功),问最小的期望花费;
解题思路
嗯,依然先按照一般 dp 的思路走起,要上 n 堂课可以申请 m 次,那么我们就设 dp [ i ][ j ] 表示前 i 堂课申请了 j 次的最小期望花费;
发现好像没法转移,因为我们只知道前几次有没有申请,并不知道这一次是否申请,换句话说我们不知道 i-1 和 i 用的是哪一间教室,那么怎么办?
再加一个维度不就好了~ 来表示第 i 堂课是否申请 。
状态设置:dp [ i ][ j ][ 0/1 ] 表示前 i 堂课申请了 j 次,第 i 堂课有没有申请(0 表示没有申请,1 表示申请了);
状态转移:
把状态设出来后,再转移就很轻松了;
就找第 i 堂课申请和不申请的情况转移一下就好了;
一 . 如果第 i 堂课不申请:
那么我们就确定了第 i 堂课会在第 c [ i ] 个教室上课;
1. 第 i-1 堂课也不申请:
我们也能确定第 i-1 堂课在第 c [ i-1 ] 个教室上课,那么这两堂课之间的期望花费是:f [ c [ i-1 ] ][ c [ i ] ]
2. 第 i-1 堂课申请:
申请是申请了,成不成功谁知道呢,所以我们要考虑全部情况:
有 k [ i-1 ] 的几率成功,那么就会换到 d [ i-1 ] 这间教室去,那么这两堂课之间的期望花费是:k [ i-1 ] * f [ d [ i-1 ] ][ c [ i ] ]
有(1 - k [ i-1 ])的几率不成功,那么还是会到 c [ i-1 ] 这间教室去上课,那么这两堂课之间的期望花费是:( 1 - k [ i-1 ] ) * f [ c [ i-1 ] ][ c [ i ] ]
那么第 i-1 堂课申请的总期望花费就是:k [ i-1 ] * f [ d [ i-1 ] ][ c [ i ] ] + ( 1 - k [ i-1 ] ) * f [ c [ i-1 ] ][ c [ i ] ]
我们在这两种情况取 min 就可以了:
dp [ i ][ j ][ 0 ] = min ( dp [ i-1 ][ j ][ 0 ] + f [ c [ i-1 ] ][ c [ i ] ] , dp [ i-1 ][ j ][ 1 ] + k [ i-1 ] * f [ d [ i-1 ] ][ c [ i ] ] + ( 1 - k [ i-1 ] ) * f [ c [ i-1 ] ][ c [ i ] ] )
二 . 如果第 i 堂课申请:
有 k [ i ] 的几率申请成功,在 d [ i ] 间教室上课;
当然有 ( 1 - k [ i ] ) 的几率申请失败,在 c [ i ] 间教室上课;
1. 第 i 间教室不申请:
我们能确定第 i-1 堂课在第 c [ i ] 间教室上,如果第 i 间教室申请成功,那么期望花费:k [ i ] * f [ c [ i-1 ] ][ d [ i ] ]
如果第 i 间教室申请失败,那么期望花费是:( 1 - k [ i ] ) * f [ c [ i-1 ] ][ c [ i ] ]
那么这种情况的总期望花费就是:k [ i ] * f [ c [ i-1 ] ][ d [ i ] ] + ( 1 - k [ i ] ) * f [ c [ i-1 ] ][ c [ i ] ]
2. 第 i 间教室申请:
这种情况就有些麻烦了(倒吸一口凉气~不慌)
(1) 两间教室都申请成功:k [ i-1 ] * k [ i ] * f [ d [ i-1 ] ][ d [ i ] ]
(2) 第 i-1 间申请成功,第 i 间申请失败:k [ i-1 ] * ( 1 - k [ i ] ) * f [ d [ i-1 ] ][ c [ i ] ]
(3) 第 i-1 间申请失败,第 i 间申请成功:( 1 - k [ i-1 ] ) * k [ i ] * f [ c [ i-1 ] ][ d [ i ] ]
(4) 两间教室都申请失败:( 1 - k [ i-1 ] ) * ( 1 - k [ i ] ) * f [ c [ i-1 ] ][ c [ i ] ]
其实很好想嘛,只是有点长而已啦~
我们在这两种情况取个 min 就可以了:
dp [ i ][ j ][ 1 ] = min ( dp [ i-1 ][ j-1 ][ 0 ] + k [ i ] * f [ c [ i-1 ] ][ d [ i ] ] + ( 1 - k [ i ] ) * f [ c [ i-1 ] ][ c [ i ] ] , dp [ i-1 ][ j-1 ][ 1 ] + k [ i-1 ] * k [ i ] * f [ d [ i-1 ] ][ d [ i ] ] + k [ i-1 ] * ( 1 - k [ i ] ) * f [ d [ i-1 ] ][ c [ i ] ] + ( 1 - k [ i-1 ] ) * k [ i ] * f [ c [ i-1 ] ][ d [ i ] ] + ( 1 - k [ i-1 ] ) * ( 1 - k [ i ] ) * f [ c [ i-1 ] ][ c [ i ] ] )
边界设置
到第一个教室是不需要花费的,所以无论第一间教室申请没申请,成功不成功,期望花费都是 0:
dp [ 1 ][ 0 ][ 0 ] = 0;(没有申请)
dp [ 1 ][ 1 ][ 1 ] = 0;(申请了)
答案
一层循环从 0~m 枚举一下申请了几次,取最小的作为答案即可。
于是我们就可以愉快的 AC 啦~
#include<iostream> #include<cstdio> #include<cmath> #include<queue> #include<cstring> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<1)+(a<<3)+(ch-'0'); ch=getchar(); } return a*x; } int n,m,v,e,x,y,w; int c[2001],d[2001],f[2001][2001]; double k[2001],dp[2001][2001][2]; int main() { n=read();m=read();v=read();e=read(); //n节课,m次申请机会,v间教室,e条边 for(int i=1;i<=n;i++) c[i]=read(); //如果不申请或申请失败所要去的教室 for(int i=1;i<=n;i++) d[i]=read(); //如果申请成功所要去的教室 for(int i=1;i<=n;i++) scanf("%lf",&k[i]); //每节课申请成功的概率 for(int i=1;i<=v;i++) //邻接矩阵存边初始化 for(int j=1;j<=v;j++) f[i][j]=1e9; for(int i=1;i<=v;i++) f[i][i]=0; for(int i=1;i<=n;i++) //dp数组初始化,求最小值赋值成无穷大 for(int j=0;j<=m;j++) dp[i][j][0]=dp[i][j][1]=1e9; dp[1][0][0]=0; //边界条件 dp[1][1][1]=0; for(int i=1;i<=e;i++) { x=read();y=read();w=read(); f[x][y]=f[y][x]=min(f[x][y],w); //注意重边的情况 } for(int k=1;k<=v;k++) //Floyd求任意两个教室之间的最短路 for(int i=1;i<=v;i++) for(int j=1;j<=v;j++) f[i][j]=min(f[i][j],f[i][k]+f[k][j]); for(int i=2;i<=n;i++) //从2开始即可 { dp[i][0][0]=dp[i-1][0][0]+f[c[i-1]][c[i]]; //一次都不申请的情况一定要单独列出来 for(int j=1;j<=m;j++) //上面一次都不申请的情况列出来了,所以j可以从1开始枚举了,就是为了怕j-1出现负数 { //冗长的转移方程 dp[i][j][0]=min(dp[i-1][j][0]+f[c[i-1]][c[i]],dp[i-1][j][1]+k[i-1]*f[d[i-1]][c[i]]+(1-k[i-1])*f[c[i-1]][c[i]]); dp[i][j][1]=min(dp[i-1][j-1][0]+k[i]*f[c[i-1]][d[i]]+(1-k[i])*f[c[i-1]][c[i]],dp[i-1][j-1][1]+k[i-1]*k[i]*f[d[i-1]][d[i]]+(1-k[i-1])*k[i]*f[c[i-1]][d[i]]+k[i-1]*(1-k[i])*f[d[i-1]][c[i]]+(1-k[i-1])*(1-k[i])*f[c[i-1]][c[i]]); } } double ans=1e9; for(int i=0;i<=m;i++) ans=min(ans,min(dp[n][i][0],dp[n][i][1])); //取最后的答案,注意i从0开始 printf("%.2lf",ans); return 0; }