P3147 [USACO16OPEN]262144

原题链接  https://www.luogu.org/problem/P3147

建议先食用无毒弱化版：P3146 [USACO16OPEN]248

这个题与上面的无毒版不同的是：数据范围变得很大，所以我们再像上个题一样定义状态是不行的了~

新状态设置： f [ i ][ j ] 表示从 j 开始能合成 i 的区间长度；

状态转移方程：

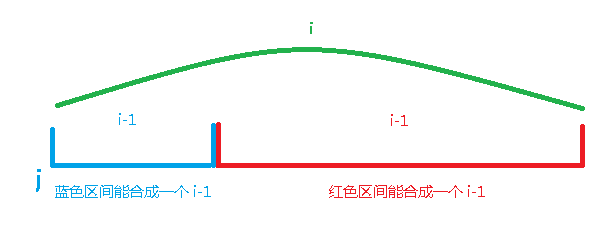
状态转移稍有些麻烦，我们看个图推一下：

按照题目所求的最大合并数，那么我们能合并就合并，最后才能合并出最大的那个数！

所以我们可以将红蓝区间继续合并，就能合成 i ；

回想一下上面状态是怎么定义的，独立思考一下转移方程 。

我们将状态转移分成两步：转移 f 数组的状态，转移 f 数组的值；

转移 f 数组的值：

这个十分简单，我们 f 数组表示的是区间长度，那么转移后的区间长度就是红蓝两个小区间的长度和呗，so easy ~

转移 f 数组的状态：

第一维：考虑到我们的 i 是由两个 i-1 转移过来的，所以第一维比较好确定，就是 i-1；

第二维：第二维表示的是起点，我们需要找到红蓝两个区间的左端点就可以了 。

显然蓝色区间的左端点是 j，红色区间的左端点就是 j + 蓝色区间的长度 ！

蓝色区间长度怎么搞啊？？？哎，我们 f 数组表示的就是区间长度唉~

So 蓝色区间的长度不就是 f [ i-1 ][ j ] ？（从 j 开始能合成 i-1 的区间长度），那么红色区间的左端点就游刃有余了，就是 j + f [ i-1 ][ j ]，那么就大功告成了~

还有再明白一点：最后合成的大区间的左端点就是蓝色区间的左端点（貌似是废话）~

f [ i ][ j ] = f [ i-1 ][ j ] + f [ i-1 ][ j + f [ i-1 ][ j ] ]；

边界条件：

这个也不是很难想，当我们第 i 个数输入的是 x 的时候，就初始化一下从 i 开始能合成 x 的区间是 1 （就是还没有合成呗~）

 

OK，就这么点了，上代码喽 (^o^)/~

#include<iostream>
#include<cstdio>
#include<queue>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
int n,x,maxn;
int f[100][300000];               //f[i][j] 表示从j开始能合成i的区间长度是多少 
int main()
{
    n=read();
    for(int i=1;i<=n;i++)         
    {
        x=read();
        f[x][i]=1;                //初始化 
    }
    for(int i=2;i<=58;i++)        //枚举第一维,最大合成的数不超过58 
    {
        for(int j=1;j<=n;j++)     //枚举第二维 
        {
            if(f[i][j]==0)        //目前没合成
            {
                if(f[i-1][j]&&f[i-1][j+f[i-1][j]])         //可以合成 
                {
                    f[i][j]=f[i-1][j]+f[i-1][j+f[i-1][j]]; //那就合成
                    maxn=i;       //肯定是越来越大的 
                }
            }           
        }
    }
    printf("%d",maxn);
    return 0;
}

再再再解释一个神奇的东东，有的童鞋可能会问第一维那个 58 是什么鬼；

其实就跟数据范围有关：

我们看到 2 ≤ N ≤ 262144，而我们像倍增一样合并，那么因为2¹⁸ = 262144

而数字的大小在 1-40 之间，那么产生的数最多也就是 40+18=58 啦~