原题链接 https://www.luogu.org/problemnew/show/P1219


想必大家在学搜索的都听说过这个题了吧?这道题十分的经典,三个月前刚开始接触的这个题,今天终于把它AC了QwQ(由此可见我是有多菜);
其实故事是这样的:在昨天的考试我由于太菜又吊车尾了,好几位神仙搜索写的很好(比如坐我右边的rank1的那位),于是我决定练练搜索,恩没错就是这样~~
下面进入正题:
由于n的范围最多不超过13,所以我们考虑用dfs。
我们开4个数组:
a[i]:第i个皇后所占的列;
b[i]:第i列有没有被占;
c[i],d[i]:对角线有没有被占;
a,b数组我们很好理解,但是c数组和d数组我们要根据棋盘的规律来深入理解:
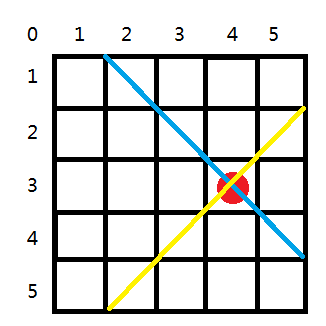



找到了怎么判断是否在同一对角线的方法后,我们再考虑怎么搜索:
我们从第一个皇后开始搜索,枚举第1~n列,只要找到了一个列和对角线没有被占领的格子就放上,然后占领这一列和对角线,用刚刚找到的规律标记上,继续搜索下一个皇后,如果我们搜完了n个皇后全放上了,方案数++,并输出前三种方案,代码如下:
#include<iostream> #include<cstdio> using namespace std; int n,tot; //tot是总方案数 int a[14],b[14],c[30],d[30]; //如果当前正在放置第n+1个皇后,说明我们已经放完了n个皇后,方案数+1 void sear(int x) //dfs,当前正在放置第x个皇后 { if(x==n+1) //如果当前正在放置第n+1个皇后,说明我们已经放完了n个皇后,方案数+1 { tot++; if(tot<=3) //输出放置前三种方案 { for(int i=1;i<=n;i++) cout<<a[i]<<" "; cout<<endl; } return ; } for(int i=1;i<=n;i++) if(!b[i]&&!c[x+i]&&!d[x-i+n]) //如果该列和对角线都没被占,放置 { a[x]=i; //第x个皇后占了第i列 b[i]=1; //宣布占领第i列 c[x+i]=1; //宣布占领对角线/ d[x-i+n]=1; //宣布占领对角线 sear(x+1); //放置下一个皇后 b[i]=0; //回溯操作,产生其他可能的方案 c[x+i]=0; d[x-i+n]=0; } } int main() { cin>>n; sear(1); //从第一个皇后开始放 cout<<tot; return 0; }