原题链接 https://www.luogu.org/problemnew/show/P1115
某大佬:天啊!普及-的题你都要写博客,太菜了吧!
主要是这个题教会了我时间复杂度O(n),空间复杂度O(1)的算法来求最大字段和。
一起来看一下吧:
我们先设一个temp来暂时存几个数的和,maxn是最大字段和,a是每次读入的数:
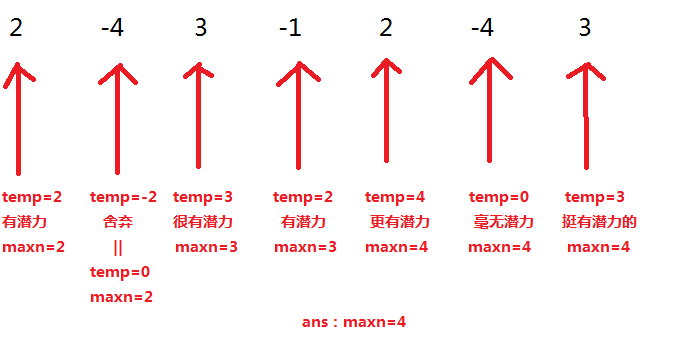
先读入一个a,记录在temp里,然后for(i=2;i<=n;i++) 读入剩下的数,如果temp小于0就将temp赋值成0,如果大于0就不用了,然后temp+=a,最后maxn=max(maxn,temp)就好啦!
#include<iostream> #include<cstdio> using namespace std; int read() { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int n,temp=0,maxn,a; int main() { n=read(); a=read(); temp=a; //temp先存着第一个数的值 maxn=-1000000; for(int i=2;i<=n;i++) { if(temp<0) temp=0; //这一步操作一定要放在读数前面,如果temp的值小于0还不如不要了 a=read(); temp+=a; //temp加上这个数的值 if(temp>maxn) maxn=temp; //取最大值 } cout<<maxn; return 0; }
解释一下正确性:
对于这个题,temp如果是小于0的话,如果不舍弃的话,再加上一个正数,肯定会拖累那个正数成为最大值(在成为最大值的道路上谁会甘心让自己加一个负数使自己变小呢?)所以我们要在读入每个数之前判断temp是不是小于0,若小于0就将它赋值成0(就是相当于舍弃了前几个数的和);若maxn>temp>0,说明temp有成为最大值的潜力,可能再加上几个正数就会一举超过最大值达到人生巅峰,所以当temp大于0时我们就不要舍弃了。下面举个例子方便理解:
但是有些毒瘤题的数据很大咋办?---------我们可以用二分!
假设我们要求区间[1,n]的最大字段和,它们的值分别是a[1],a[2]……,a[n],我们可以将区间[1,n]分成两个长度相等的小区间[1,n/2]和[n/2+1,n],那么这个最大子段有三种情况:
1. 最大子段在区间[1,n/2]里;
2. 最大子段再区间[n/2+1,n]里;
3. 最大子段的左端点再区间[1,n/2],右端点在[n/2+1,n]里;
对于第一和第二种情况,我们可以递归解决,我们重点看第三种情况:

我们已经知道两个端点分别在两个小区间,设这两个端点为p,q,那么区间[p,n/2]和区间[n/2+1,q]这一段一定是连续被包含在最大子段里的,且要是整个子段最大,那么久尽量让左子段和右子段最大,所以我们可以从n/2分别往左和往右扫求出最大子段,再加起来就是整个区间的最大子段。