//bfs求最小行走步数模板题
TOJ-2481: Knight Moves
描述
Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
For people not familiar with chess, the possible knight moves are shown in Figure 1.
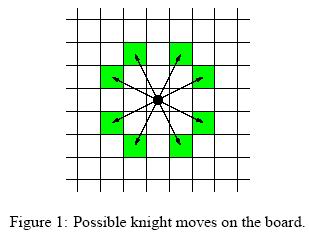
输入
The input begins with the number n of scenarios on a single line by itself.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, ..., l-1}*{0, ..., l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
输出
For each scenario of the input you have to calculate the minimal amount of knight moves which are necessary to move from the starting point to the ending point. If starting point and ending point are equal,distance is zero. The distance must be written on a single line.
样例输入
3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
样例输出
5
28
0
#include<bits/stdc++.h> using namespace std; int a,b,c,d,size1; int drec[9][2]={{-2,1},{-2,-1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}}//走动方式; const int N=310; int vis[N][N]; struct node { int x,y,step; node(){} node(int x1,int y1,int step1):x(x1),y(y1),step(step1){} }; void bfs(int x,int y) { memset(vis,0,sizeof(vis)); vis[x][y]=1; queue<node> q; q.push(node(x,y,0)); while(!q.empty()) { node a=q.front(); q.pop(); for(int i=0;i<8;i++) { int xx=a.x+drec[i][0]; int yy=a.y+drec[i][1]; if(xx>=0&&xx<size1&&yy>=0&&yy<size1&&(vis[xx][yy]==0))//可以行走的条件 { vis[xx][yy]=1; q.push(node(xx,yy,a.step+1)); if(xx==c&&yy==d) { cout<<a.step+1<<endl; return; } } } } } int main() { int t ; cin>>t; while(t--) { cin>>size1; cin>>a>>b>>c>>d; if(a==c&&d==b) { cout<<0<<endl; continue; } bfs(a,b); } }
//bfs 相对于 dfs 来说走的少了很多所以时间上也更快一点,因为dfs要走出所有的路,bfs只是同时在每一条路上走出一步;
下面是dfs 代码 如果用dfs代码题交这个题是超时的;
#include<bits/stdc++.h> using namespace std; int a,b,c,d,size1; int drec[9][2]={{-2,1},{-2,-1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}}; const int N=301; int vis[N][N]; int viss[N][N]; int minn=100000; void dfs(int x,int y,int step) { if(step>=viss[x][y]||step>=minn) return; viss[x][y]=step; for(int i=0;i<8;i++){ int xx=x+u[i][0]; int yy=y+u[i][1]; if(xx>=0&&xx<=size1&&yy>=0&&yy<=size1&&(!vis[xx][yy])){ if(xx==c&&yy==d){ minn=min(step+1,minn); return ; } vis[xx][yy]=1; dfs(xx,yy,step+1); vis[xx][yy]=0; } } } int main() { ios::sync_with_stdio(false); int t; cin>>t; while(t--) { minn=1000000; cin>>size1; cin>>a>>b>>c>>d; if(a==c&&b==d) { cout<<0<<endl; continue; } memset(viss,0x3f3f3f3f,sizeof(viss)); dfs(a,b,0); cout<<minn<<endl; } }