图像分类可说是计算机视觉中的基础任务同时也是核心任务,做好分类可为检测,分割等高阶任务打好基础。
本节课主要讲了两个内容,K近邻和线性分类器,都是以猫的分类为例。
一. K近邻
以猫的分类为例,一张含有猫的图片,也不过就是一堆像素点

问题就在于给你一堆点,如何判断出是一只猫,在很久很久以前,这还真是个超级难题,何况不同的猫,像素点完全不一致
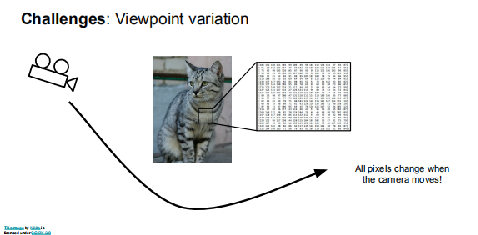
具体来说可有以下几种
光照,目标的形变,遮挡,背景杂乱,类内差异等等。





如何利用K近邻算法解决这一问题呢,K近邻,就是将你要判别的目标与已有的大量目标进行比较,与谁最近,就是哪一类,有点物以类聚的意思,不过,只选
取最近的一张作为参照有致命缺陷,保不准就有哪只狗与该目标相近,于是你就把这只猫判断为狗了,所以保险起见,会取最近的K张图片作为参照,其中哪一类
最多,就归属于哪一类,这种做法难说完美,不过比一张靠谱多了。
下面以cifar-10数据集为例展示下k近邻算法。


cifar-10数据集包含10类目标,图像尺寸均为32x32,在充满着高清无码大图的现代社会,着实有些复古。
左图就是数据集的一个图示,右图是根据测试图片选取的10张最近图像,由于图像太小,有些看不清。
那么什么样的图像是比较接近的,或者说如何测量两张图象的距离呢
一种测距方式是L1距离,也叫曼哈顿距离,举例来说,坐标系中两个点(1,1)和(2,2),L1=(2-1)+(2-1)=2,通俗点说你只能直来直去,不能斜着来。
不过对于图像而言,L1并不是一种合适的测距方式,图像不过是一堆像素,你完全可以构造两个L1距离相同的图像,其像素排列却是有很多变化。
像下面这样,右侧三张图与最左侧的距离是一样的,然而三张图却各有不同。

具体计算方式可以像下面这样。
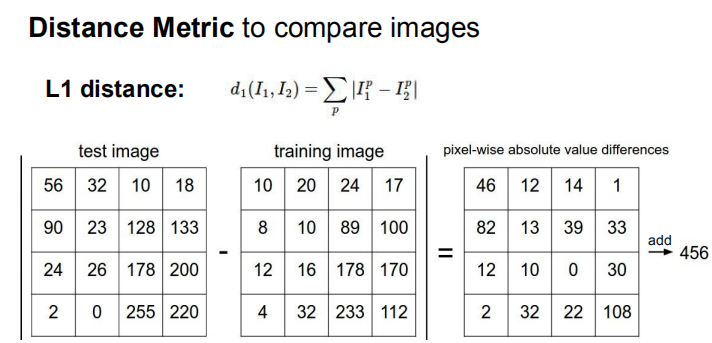
L2距离也许是一种更合适的方式,L2距离,也称欧式距离,L2=√((2-1)**2+(2-1)**2)=√2
在课程的k近邻算法展示主页上,可以自行感受下L1与L2的区别,http://vision.stanford.edu/teaching/cs231n-demos/knn/
除了距离的度量方式,K值的选择也是一个关键因素,很大程度上决定着k近邻算法的好坏,通常不会取为1,只参照一张最相近的的图像来判断测试图像有很大的偶然性。
下图是最好的说明。
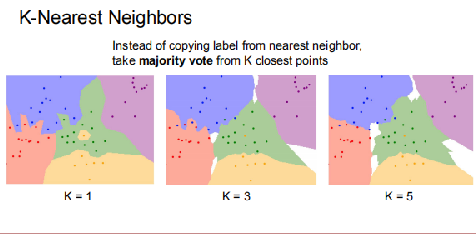
在上图中,不同颜色代表不同类别,标出的点是训练数据集,那些没有点的颜色区代表你的测试图像,根据最近邻原则分类,并上色。
可以看到,k=1时类别边界崎岖不平,有些突起已经深入其它类内,显然不合理,再注意绿色中间的黄色区域,代表着该点周围的点被归为黄色类,只因为与该黄色点最近,
显然也是错误的,k=1时分类效果易受噪声影响,具有偶然性。随着k的加大,类别边界趋于平滑,给人的感觉也更加合理,出现的白色区域根据上面的演示网址所说,是投票
数均等的区域,就是无法决策的区域。
那么如何选择测距方式和K值呢,在机器学习里,这些无法训练得来,需要手动设定的参数成为超参数,超参数的设置需要通过实验试探得到,具体需要根据数据集划分来决定。
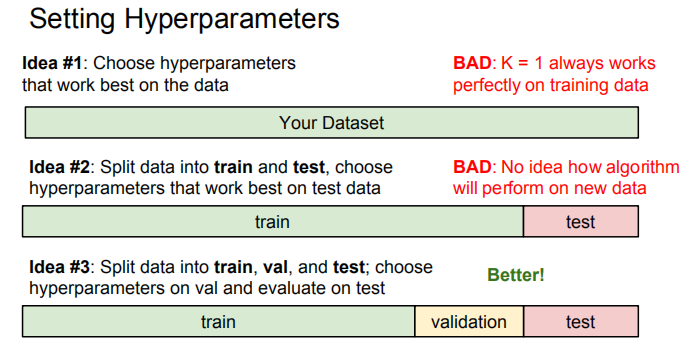
如上图所示,数据集最佳划分为训练集,验证集,测试集,仅有训练集和验证集都无法保证良好的泛化能力(也就是应用在其它未出现过的数据上),当然,有测试集也无法一定确保良好的泛化能力,但还是比前两个要好很多。
还有一种划分方式为交叉验证,一般用于小型数据集,数据集既能用来训练,又能用来验证。
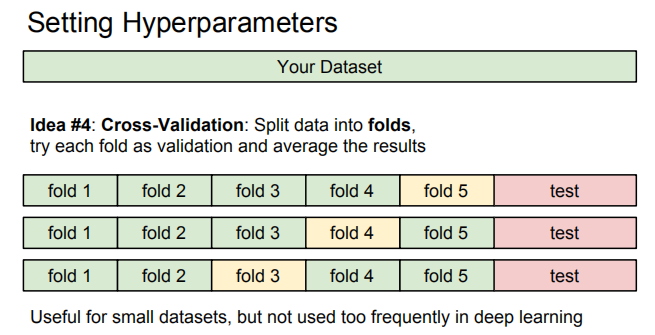
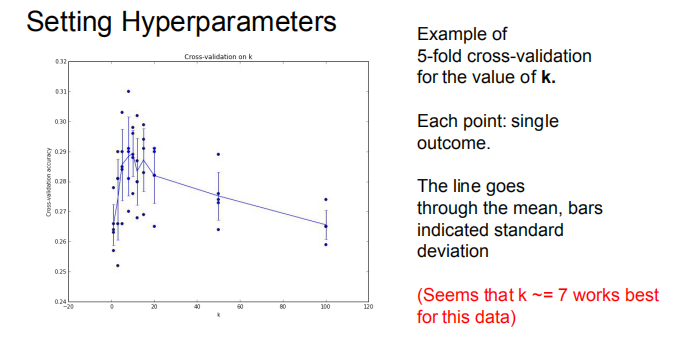
下图是针对k近邻的5折交叉验证方式,k=7时取得最好结果。
最后总结下,k近邻作为一种简单的分类算法,有着其天然缺陷,一是k值的设置需要实验来确定,二是需要事先存储训练数据集以用来分类,三是致命的一点,每次测试都需要与所有数据进行距离计算,太耗计算资源。
那么,有没有其它办法呢,有,就是接下来要讲的线性分类器。
二.线性分类器
线性分类器基于简单的代数运算,就是相乘相加,以一张猫的图片为例,每一个像素点都有像素值,对每一个点乘以一个权重再相加,就可以输出一个标量值,当你为这个值赋予一定含义的时候,比如正代表动物,负代表其它,那它就构成了一个简单的线性分类器。
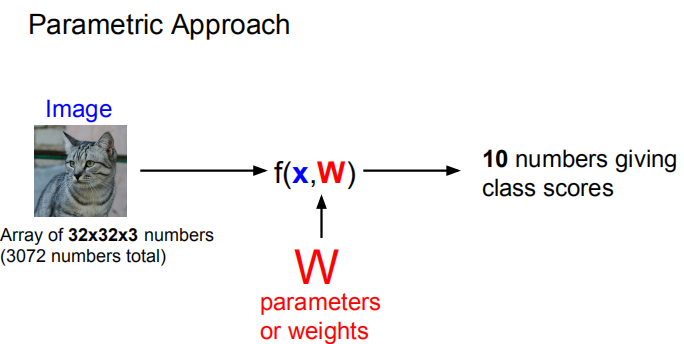
同样道理,你也可以输出一个向量,如果进行10分类,则可以输出10维向量。
再具体点,像下面这样。
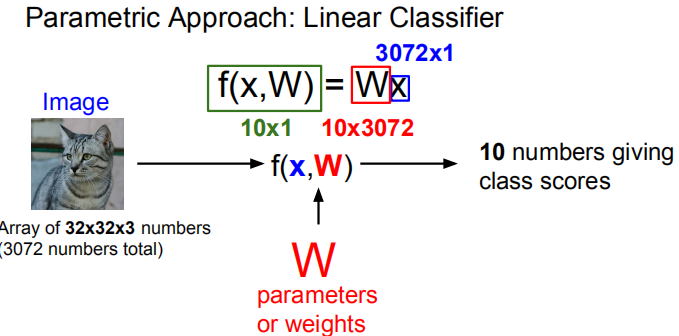
下面这样
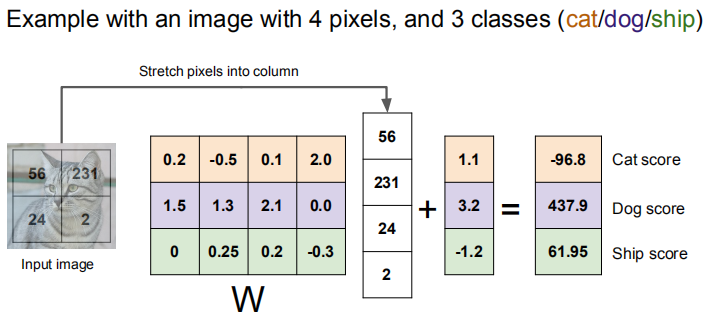
可以将整幅图像看成高维空间中的一点,线性分类器就是点与点之间的分类平面,如果是猫狗二分类,猫的点在一边,狗的点在另一边,中间是分类平面。
画出来就像下面这样。
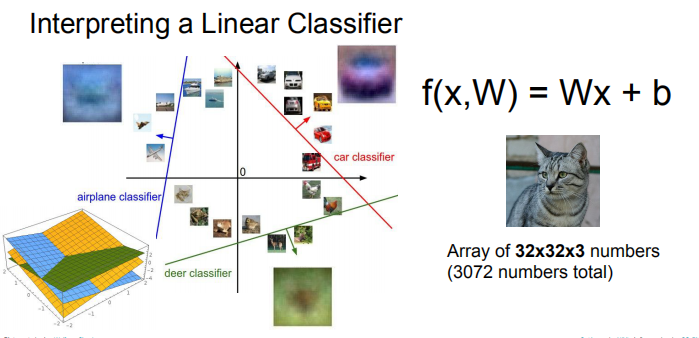
有了这样的想法,下一步就是设置合适的权重w与偏置b,如何设置涉及到损失函数与最优化的学问,那是下堂课要讲的故事。