1.变分自编码
变分是数学上的概念,大致含义是寻求一个中间的函数,通过改变中间函数来查看目标函数的改变。变分推断是变分自编码的核心,那么变分推断是要解决的是什么问题??
问题描述如下,假如我们有一批样本X,这个时候,我们想生成一批和它类似的样本,且分布相同,这个时候我们该怎么办呢?
1.如果我们知道样本的分布的情况下,这个事情就好办了,先生成一批均匀分布的样本,通过分布的具体形式与均匀分布之间的关系,生成一批新的样本。
2.如果我们不知道样本分布的情况下,仍然可以通过一些方法得到类似的样本,例如MCMC过程,Gibbs-Sample等
更加详细的推断和过程,可以在LDA数学八卦来寻找答案。
神经网络拥有拟合出任意函数的特点,那么使用它来拟合我们的数据分布可以不?答案是肯定的,AutoEncoder的就是为了尽可能拟合原始数据而服务的,但是一般的AutoEncoder在工程中大部分只是被用来作为降维的手段,并没有产生新样本的功能,那就是VAE(变分自编码)的能解决的问题了。
1.1 变分推断
限于本人数学造诣只是二把刀,下面的论断大部分来自网上相关博客,引用已经写在下面,有疑问,大家勿喷。下面的公式来自于 VARIATIONAL INFERENCE & DEEP LEARNING: A NEW SYNTHESIS

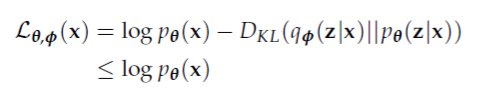
公式的推倒主要使用了贝叶斯公式和詹森不等式,有兴趣的同学可以尝试一下。下面我们只分析这个结果,以及用途。
变分推断给出了一个下界,我们可以通过最大化$L_{ heta,phi }(x)$ 来同时获得$phi , heta $的最优解,从而获得需要逼近的数据分布。比较有趣的是$D_{KL}(q_{phi }(z|x)||p_{ heta }(z|x))$决定了两个“距离”:
- KL散度决定了先验假设的分布和真实分布的相似性。
- $L_{ heta,phi }(x)$ 和最大相似似然函数$log p_{ heta }(x)$之间的间隔。
所以最大化KL散度既能使得$q_{phi }(z|x)$趋近于真实的分布$p_{ heta }(z|x)$,又使得$L_{ heta,phi }(x)$和$log p_{ heta }(x)$的“间隔”变得更小。
1.2 VAE的学习过程
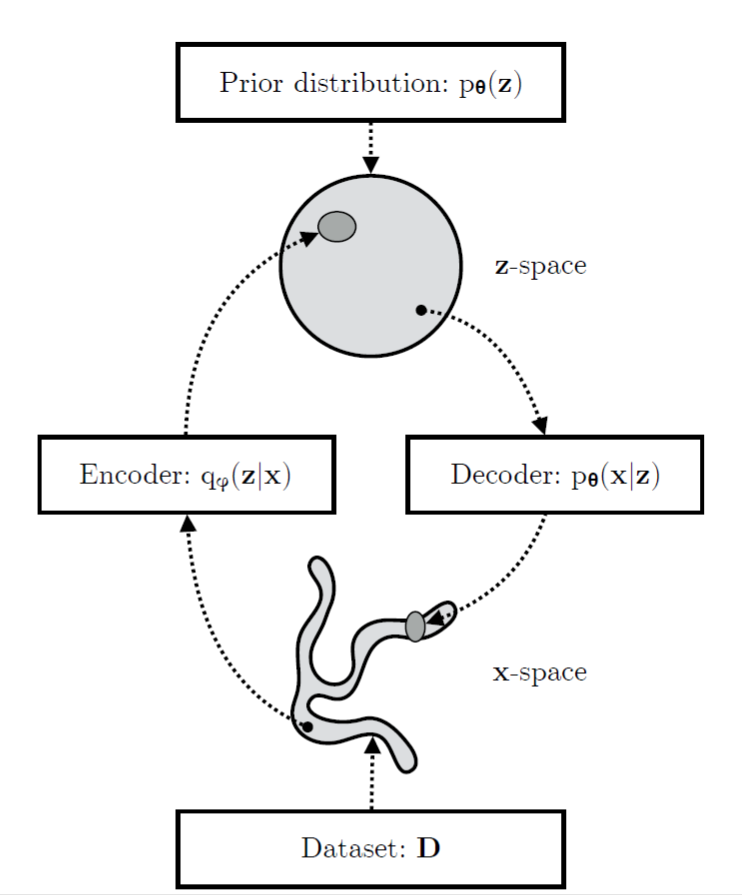
如上面幅图显示的如此,VAE包含两部分:Encoder和Decoder,前者又被成为推理模型,后者又被成为生成模型。正常来说$q_{D}(x)$的分布是比较复杂的,而映射之后的z空间在比较简单(通常假设为我们常见的分布,像高斯分布),生成模型学习一个联合分布$p_{ heta }(x,z)=p_{ heta }(z)p_{ heta }(x|z)$,该联合分布分解为两部分,首先是z空间的先验分布$p_{ heta }(z)$和随机解码器$p_{ heta }(x|z)$。

上面这张图给出了模型训练的伪代码,值得注意的是下面两点:
- 在实际工程当中,我们经常假设z服从高斯分布,从理论上讲可以是任何分布,也可以是均匀分布,但是均匀分布在训练过程中计算KL散度可能得到无穷大值。
- 中间采样的过程是怎么加入到神经网络的BP算法中的?这个地方是作者采用了 reparemerization 的方法,在实际训练中$z=g(varepsilon ,phi ,x)$满足该分布,其中$varepsilon$是独立于$phi$和x的,经常把$varepsilon$ 看作原始分布的一种噪音,这样随机独立的噪音可以与模型训练无关,我们只关注于$phi$和x,抽样的过程则是不同$varepsilon$ 的由z分布生成的样本。
1.3 比较常见的VAE模型
隐含变量z服从高斯分布,对应的目标函数变成
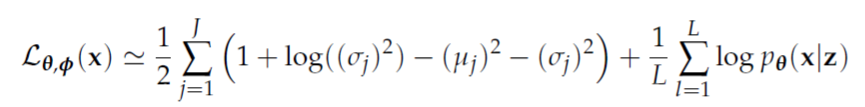
中间的抽样过程如下图所示:

训练模型时值得注意
- 生成模型$p_{ heta }(x|z)$也经常假设一种分布,如果是二值的数据的话,我们经常假设为伯努利分布;如果是真实的数据的话,经常假设为高斯分布。
- 生成模型的输出,都是独立的,也就是说神经网络的最后一层的每个输出不能使用softmax这种彼此互斥的输出的函数。
- 输入模型的数据建议归一化一下,因为网上有些代码中会使用mse作为对$p_{ heta }(x)$的等价,其实拟合的输出是高斯分布的情况(具体证明参见Pattern Recognition and Machine Learning 第5.2章节),对于非归一化的数据,mse倾向于优化变化范围大的列。归一化之后,可以使用binary_cross-entropy (这里使用的是多输出的情况)。
1.4 网上的例子
https://github.com/keras-team/keras/blob/master/examples/variational_autoencoder.py
https://github.com/tensorflow/probability/blob/master/tensorflow_probability/examples/vae.py
第一个着重于实践,是使用keras来写的,后者是使用tensorflow写的,比较符合数学上的公式推导,我们来一起分析一下代码的重点部分
def make_encoder(activation, latent_size, base_depth): """Creates the encoder function. Args: activation: Activation function in hidden layers. latent_size: The dimensionality of the encoding. base_depth: The lowest depth for a layer. Returns: encoder: A `callable` mapping a `Tensor` of images to a `tfd.Distribution` instance over encodings. """ conv = functools.partial( tf.keras.layers.Conv2D, padding="SAME", activation=activation) encoder_net = tf.keras.Sequential([ conv(base_depth, 5, 1), conv(base_depth, 5, 2), conv(2 * base_depth, 5, 1), conv(2 * base_depth, 5, 2), conv(4 * latent_size, 7, padding="VALID"), tf.keras.layers.Flatten(), tf.keras.layers.Dense(2 * latent_size, activation=None), ]) def encoder(images): images = 2 * tf.cast(images, dtype=tf.float32) - 1 net = encoder_net(images) return tfd.MultivariateNormalDiag( loc=net[..., :latent_size], scale_diag=tf.nn.softplus(net[..., latent_size:] + _softplus_inverse(1.0)), name="code") return encoder
首先是encoder,encoder部分的最后一层的大小是2*lant_size,其中在构建高斯分布的时候,0~ lant_size个输出作为了Mean,后lant_size个输出作为了方差。
def make_decoder(activation, latent_size, output_shape, base_depth): """Creates the decoder function. Args: activation: Activation function in hidden layers. latent_size: Dimensionality of the encoding. output_shape: The output image shape. base_depth: Smallest depth for a layer. Returns: decoder: A `callable` mapping a `Tensor` of encodings to a `tfd.Distribution` instance over images. """ deconv = functools.partial( tf.keras.layers.Conv2DTranspose, padding="SAME", activation=activation) conv = functools.partial( tf.keras.layers.Conv2D, padding="SAME", activation=activation) decoder_net = tf.keras.Sequential([ deconv(2 * base_depth, 7, padding="VALID"), deconv(2 * base_depth, 5), deconv(2 * base_depth, 5, 2), deconv(base_depth, 5), deconv(base_depth, 5, 2), deconv(base_depth, 5), conv(output_shape[-1], 5, activation=None), ]) def decoder(codes): original_shape = tf.shape(codes) # Collapse the sample and batch dimension and convert to rank-4 tensor for # use with a convolutional decoder network. codes = tf.reshape(codes, (-1, 1, 1, latent_size)) logits = decoder_net(codes) logits = tf.reshape( logits, shape=tf.concat([original_shape[:-1], output_shape], axis=0)) return tfd.Independent(tfd.Bernoulli(logits=logits), reinterpreted_batch_ndims=len(output_shape), name="image") return decoder
在decoder中我们看到,输出都是彼此独立的,且是伯努利分布。
approx_posterior = encoder(features)//数据进行encoder处理,得到高斯分布的参数 approx_posterior_sample = approx_posterior.sample(params["n_samples"])//从得到的高斯函数中抽样,并没有使用重参数的方法 decoder_likelihood = decoder(approx_posterior_sample)//将抽样的样本输入给decoder,得到伯努利分布的输出 distortion = -decoder_likelihood.log_prob(features)//得到-logp(x) latent_prior = make_mixture_prior(params["latent_size"], params["mixture_components"])//得到一个标准的多维高斯分布,主要是为了计算KL的时候使用 if params["analytic_kl"]: rate = tfd.kl_divergence(approx_posterior, latent_prior) else: rate = (approx_posterior.log_prob(approx_posterior_sample) - latent_prior.log_prob(approx_posterior_sample))//该方法是指另外一种衡量生成分布和高斯分布之间距离的形式 avg_rate = tf.reduce_mean(rate) tf.summary.scalar("rate", avg_rate) elbo_local = -(rate + distortion) elbo = tf.reduce_mean(elbo_local) loss = -elbo
上述则是loss函数的组成了,其中features就是原始输入。
注:
- 输入的数据是binarized_mnist,所以输出用的伯努利分布,伯努利之前的输出层并没有任何激活函数。
2.VAE条件自编码
vae条件自编码,解决的是一个什么问题呢?在经典的生成样本的问题中,例如我们已经根据minist 数据集训练了一个vae,我想得到数字"3"的生成的图片,如何得到呢?很显然,仅仅依靠得到的vae是无法得到的,可能有人会问,我们遍历一组随机的输入,肯定能得到想要的样本,但是却不是终极解决方案。
条件自编码的大概意思就是在encoder端和decoder端都输入label信息(eg 角度信息,明暗信息)等额外信息,来控制我们想要生成什么类型的样本。示意图如下:
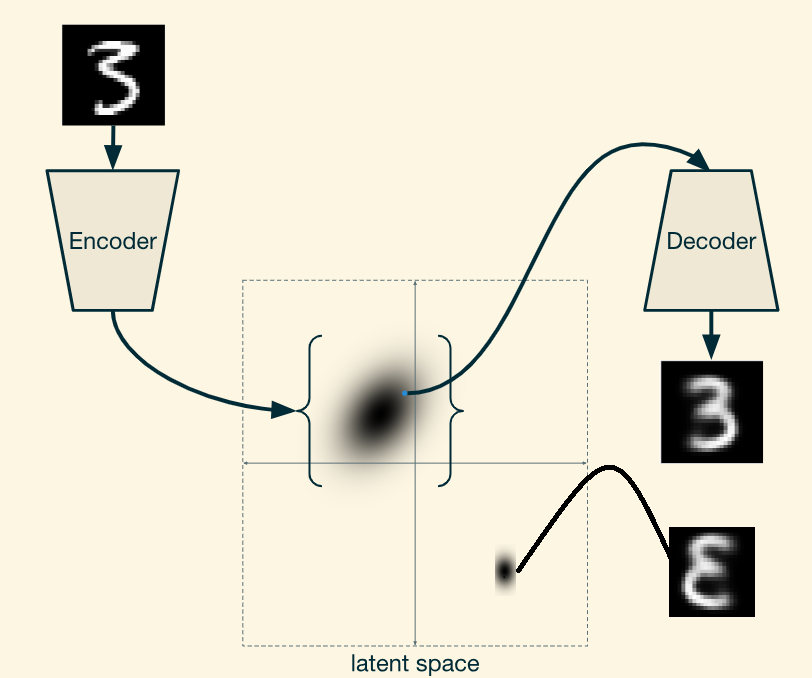
输入额外信息之后的encoder得到的latent space只满足在额外信息下的 高斯分布(假如我们在隐式空间上生成的是高斯分布),注意和没有额外条件信息下生成的高斯分布的差异,如下:
我们看一下条件vae产生的整体的分布是个什么鬼?下图来自于minist的例子
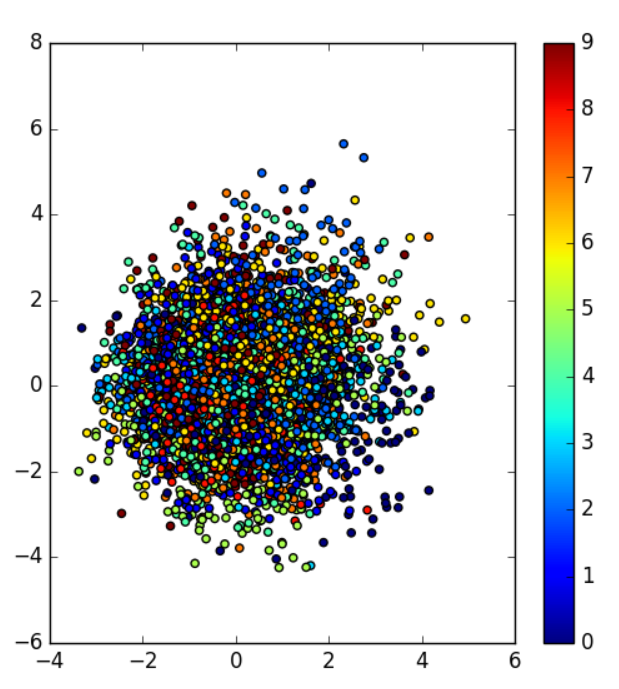
上图其实分布是相当乱,但是细心的朋友可以看到,每一种颜色近似呈现高斯分布。
介绍就到此为止吧,我们看一哈,如果用keras怎么实现它。
样例代码 https://github.com/nnormandin/Conditional_VAE/blob/master/conditional_vae.py
# encoder inputs X = Input(shape=(784, )) cond = Input(shape=(n_y, )) # merge pixel representation and label inputs = concatenate([X, cond]) # dense ReLU layer to mu and sigma h_q = Dense(512, activation='relu')(inputs) mu = Dense(n_z, activation='linear')(h_q) log_sigma = Dense(n_z, activation='linear')(h_q)
在encoder的输入中加入y的输入
# dense ReLU to sigmoid layers decoder_hidden = Dense(512, activation='relu') decoder_out = Dense(784, activation='sigmoid') h_p = decoder_hidden(z_cond) outputs = decoder_out(h_p) # define cvae and encoder models cvae = Model([X, cond], outputs) encoder = Model([X, cond], mu) # reuse decoder layers to define decoder separately d_in = Input(shape=(n_z+n_y,)) d_h = decoder_hidden(d_in) d_out = decoder_out(d_h)
在decoder中加入y的信息,其余的都不变
3. 使用VAE做异常检测
在参考4的这篇论文中,作者提出了使用VAE的重建概率来进行异常检测。所谓异常检测,有别于监督学习的概念,异常检测属于无监督学习。既然是无监督,那么你是不知道它学出来的是什么的。举个栗子,假如你想要识别手机账号登陆异常的行为,但是你只有用户的年龄这个特征,能不能搞呢?答案是肯定的,肯定可以使用异常检测算法,识别出哪些是可能的异常的,但是识别出来的东西,你敢用吗??所以异常检测的关键不在于算法,而在于特征,选择的特征和要做的事情要足够相关。而无监督的结果是没办法评估的,所以一般的异常检测方法,都是先筛选一批特征训练模型,然后上线测试,再不停地迭代,上线的时候通过拦截率或者成本、营收等指标来确定拦截的阈值,所以异常检测并不期望能找出所有的有问题的数据,往往作为第一道关卡来筛选掉一批明显有问题的数据。
废话少说,让我们看看它是怎么做异常检测的。文章先介绍了使用AE做异常检测,出发点是AE的拟合过程,适用于大部分数据,对于极个别的异常数据,它们的重建误差会明显大于其他的正常数据,从中我们可以看出,异常数据有两个特点。第一,异常数据是少量的;第二,异常数据是明显区别于大部分人的。做法也很粗暴,先训练一个AE,然后挨个输出一下重建概率就可以了,算法伪代码如下:

参数$alpha$ 依赖于场景的拦截比例。
那么VAE的做法和AE类似,也是先训练一个VAE模型,然后使用loss函数的重建概率,作为异常检测的判断函数。伪代码如下:

区别于AE的地方是,后面的重构概率是基于某个分布生成的,作者阐明这也是它的优势之一,能够具有更好的鲁棒性。那么它的优势之二呢,它的输出是概率,并没有AE的输入那种存在各列特征分布区间不一致导致的重建误差存在偏差,也就是特征可能存在不同的权重。
接下来就是效果咯:

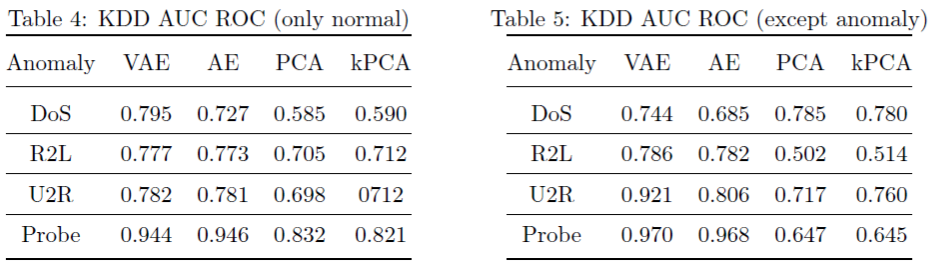
从效果上看,大部分都是VAE比AE要好一些,但是也存在个别特殊的情况,不能一棒子打死。
如果还不过瘾,来一个kaggle的例子??
还没完,一大波的源码如下:
https://github.com/chen0040/keras-anomaly-detection
参考:
1. https://ynuwm.github.io/2017/05/14/%E8%87%AA%E7%BC%96%E7%A0%81%E5%99%A8AutoEncoder/
2. https://wiseodd.github.io/techblog/2016/12/10/variational-autoencoder/