from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
def split_train(iris_split):
iris_data=iris_split
np.random.shuffle(iris_data)
iris_train=iris_data[0:35,:]
iris_test=iris_data[35:50,:]
return iris_train,iris_test
def med(iris_train):
x1=0
x2=0
x3=0
x4=0
for i in range(35):
x1=x1+iris_train[i,0]
x2=x2+iris_train[i,1]
x3=x3+iris_train[i,2]
x4=x1+iris_train[i,3]
x1=x1/35
x2=x2/35
x3=x3/35
x4=x4/35
return x1,x2,x3,x4
def avg(iris_1,iris_2,n):
for i in range(n-1):
sumtp=0
sumtn=0
sumfp=0
sumfn=0
x_train,x_test = split_train(iris_1)
y_train,y_test = split_train(iris_2)
x_v=med(x_train)
y_v=med(y_train)
tp,tn,fp,fn=assess(x_test,y_test,x_v,y_v)
sumtp=sumtp+tp
sumtn=sumtn+tn
sumfp=sumfp+fp
sumfn=sumfn+fn
p=(tp+tn)/(tp+tn+fp+fn)
return p
def assess(x_test,y_test,x_v,y_v):
tp=0
tn=0
fp=0
fn=0
for i in range(15):
dxx=((x_test[i,0]-x_v[0])**2+(x_test[i,1]-x_v[1])**2+(x_test[i,2]-x_v[2])**2+(x_test[i,0]-x_v[3])**2)**0.5
dxy=((x_test[i,0]-y_v[0])**2+(x_test[i,1]-y_v[1])**2+(x_test[i,2]-y_v[2])**2+(x_test[i,0]-y_v[3])**2)**0.5
if(dxx<dxy):
tp=tp+1
elif(dxx>dxy):
fn=fn+1
dyx=((y_test[i,0]-x_v[0])**2+(y_test[i,1]-x_v[1])**2+(y_test[i,2]-x_v[2])**2+(y_test[i,0]-x_v[3])**2)**0.5
dyy=((y_test[i,0]-y_v[0])**2+(y_test[i,1]-y_v[1])**2+(y_test[i,2]-y_v[2])**2+(y_test[i,0]-y_v[3])**2)**0.5
if(dyx>dyy):
tn=tn+1
elif(dyx<dyy):
fp=fp+1
return tp,tn,fp,fn
iris=datasets.load_iris()
x = iris.data[:,1]
y = iris.data[:,3]
species = iris.target
x_min,x_max = x.min() - .5,x.max() + .5
y_min,y_max = y.min() - .5,y.max() + .5
plt.figure()
plt.title('Iris DataSet - Classfication By Sepal Sizes')
plt.scatter(x,y,c=species)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(x_min,x_max)
plt.ylim(y_min,y_max)
plt.xticks()
plt.yticks()
plt.show()
iris_1=iris.data[0:50:,]
iris_2=iris.data[50:100,]
p=avg(iris_1,iris_2,10)
print(p)
U,Sigma,V = np.linalg.svd(iris.data)
iris_1=iris.data[50:100:,]
iris_2=iris.data[100:150,]
p=avg(iris_1,iris_2,10)
print(p)
def split(iris_data,i):
np.random.shuffle(iris_data)
iris_test=iris_data[i:i+9,:]
iris_test=iris_test.tolist()
iris_list=iris_data.tolist()
iris_train=iris_list
isis_train=[item for item in iris_list if item not in iris_test]
iris_test=np.array(iris_test)
iris_train=np.array(iris_train)
return iris_train,iris_test
def feature(iris_1,iris_2,iris_3):
sumx1=0
sumx2=0
for i in range(40):
x1=(iris_1[i,0]+iris_1[i,1]+iris_2[i,0]+iris_2[i,1]+iris_3[i,0]+iris_3[i,1])/3
x2=(iris_1[i,2]+iris_1[i,3]+iris_2[i,2]+iris_2[i,3]+iris_3[i,2]+iris_3[i,3])/3
sumx1=sumx1+x1
sumx2=sumx2+x2
x1=sumx1/40
x2=sumx2/40
return x1,x2
def train(iris_1,iris_2,iris_3,x,y):
numx_00=0
numx_01=0
numx_10=0
numx_11=0
numy_00=0
numy_01=0
numy_10=0
numy_11=0
numz_00=0
numz_01=0
numz_10=0
numz_11=0
for i in range(40):
if((iris_1[i,0]+iris_1[i,1])>x):
if((iris_1[i,2]+iris_1[i,3])>y):
numx_11=numx_11+1
else:
numx_10=numx_10+1
else:
if((iris_1[i,2]+iris_1[i,3])>y):
numx_01=numx_01+1
else:
numx_00=numx_00+1
if((iris_2[i,0]+iris_2[i,1])>x):
if((iris_2[i,2]+iris_2[i,3])>y):
numy_11=numy_11+1
else:
numy_10=numy_10+1
else:
if((iris_2[i,2]+iris_2[i,3])>y):
numy_01=numy_01+1
else:
numy_00=numy_00+1
if((iris_3[i,0]+iris_3[i,1])>x):
if((iris_3[i,2]+iris_3[i,3])>y):
numz_11=numz_11+1
else:
numz_10=numz_10+1
else:
if((iris_3[i,2]+iris_3[i,3])>y):
numz_01=numz_01+1
else:
numz_00=numz_00+1
sum_11=numx_11+numy_11+numz_11
sum_10=numx_10+numy_10+numz_10
sum_01=numx_01+numy_01+numz_01
sum_00=numx_00+numy_00+numz_00
p1_11=(numx_11)/40*1/3/((sum_11/120)+0.001) #第一类中拥有特征1和特征2的个数用numx_11,有特征1没特征2就numx_10,sum_11则代表3类中有特征1和特征2的总数
p1_10=(numx_10)/40*1/3/((sum_11/120)+0.001) #由于我在划分训练集的时候每一类的比例都一样,所以每一类个数都为40
p1_01=(numx_01)/40*1/3/((sum_11/120)+0.001) #在实际运行过程中,可能因为我选的特征比较不合适或者数据比较少,会有等于0的情况导致之后算后验概率报错,所以都加上0.001
p1_00=(numx_00)/40*1/3/((sum_11/120)+0.001)
p2_11=(numy_11)/40*1/3/((sum_11/120)+0.001)
p2_10=(numy_10)/40*1/3/((sum_11/120)+0.001)
p2_01=(numy_01)/40*1/3/((sum_11/120)+0.001)
p2_00=(numy_00)/40*1/3/((sum_11/120)+0.001)
p3_11=(numz_11)/40*1/3/((sum_11/120)+0.001)
p3_10=(numz_10)/40*1/3/((sum_11/120)+0.001)
p3_01=(numz_01)/40*1/3/((sum_11/120)+0.001)
p3_00=(numz_00)/40*1/3/((sum_11/120)+0.001)
return p1_11,p2_11,p3_11,p1_10,p2_10,p3_10,p1_01,p2_01,p3_01,p1_00,p2_00,p3_00
def test(iris1_test,iris2_test,iris3_test,x,y,p1_11,p2_11,p3_11,p1_10,p2_10,p3_10,p1_01,p2_01,p3_01,p1_00,p2_00,p3_00):
n=0
for i in range(10):
x_t=iris_1[i,0]+iris_1[i,1]
y_t=iris_1[i,2]+iris_1[i,3]
if(x_t>x):
if(y_t>y):
if(p1_11==max(p1_11,p2_11,p3_11)):
n=n+1
if(x_t>x):
if(y_t<y):
if(p1_10==max(p1_10,p2_10,p3_10)):
n=n+1
if(x_t<x):
if(y_t>y):
if(p1_01==max(p1_01,p2_01,p3_01)):
n=n+1
if(x_t<x):
if(y_t<y):
if(p1_00==max(p1_00,p2_00,p3_00)):
n=n+1
x_t=iris_2[i,0]+iris_2[i,1]
y_t=iris_2[i,2]+iris_2[i,3]
if(x_t>x):
if(y_t>y):
if(p2_11==max(p1_11,p2_11,p3_11)):
n=n+1
if(x_t>x):
if(y_t<y):
if(p2_10==max(p1_10,p2_10,p3_10)):
n=n+1
if(x_t<x):
if(y_t>y):
if(p2_01==max(p1_01,p2_01,p3_01)):
n=n+1
if(x_t<x):
if(y_t<y):
if(p2_00==max(p1_00,p2_00,p3_00)):
n=n+1
x_t=iris_3[i,0]+iris_3[i,1]
y_t=iris_3[i,2]+iris_3[i,3]
if(x_t>x):
if(y_t>y):
if(p3_11==max(p1_11,p2_11,p3_11)):
n=n+1
if(x_t>x):
if(y_t<y):
if(p3_10==max(p1_10,p2_10,p3_10)):
n=n+1
if(x_t<x):
if(y_t>y):
if(p3_01==max(p1_01,p2_01,p3_01)):
n=n+1
if(x_t<x):
if(y_t<y):
if(p3_00==max(p1_00,p2_00,p3_00)):
n=n+1
return n
def kz(iris_1,iris_2,iris_3):
m=0
for i in range(10):
iris1_train,iris1_test=split(iris_1,i)
iris2_train,iris2_test=split(iris_2,i)
iris3_train,iris3_test=split(iris_3,i)
x,y=feature(iris_1,iris_2,iris_3)
p1_11,p2_11,p3_11,p1_10,p2_10,p3_10,p1_01,p2_01,p3_01,p1_00,p2_00,p3_00=train(iris1_train,iris2_train,iris3_train,x,y)
n=test(iris1_test,iris2_test,iris3_test,x,y,p1_11,p2_11,p3_11,p1_10,p2_10,p3_10,p1_01,p2_01,p3_01,p1_00,p2_00,p3_00)
m=m+n
m=m/10
p=m/30
return p
iris_1=iris.data[0:50,:]
iris_2=iris.data[50:100,:]
iris_3=iris.data[100:150,:]
p=kz(iris_1,iris_2,iris_3)
print(p)
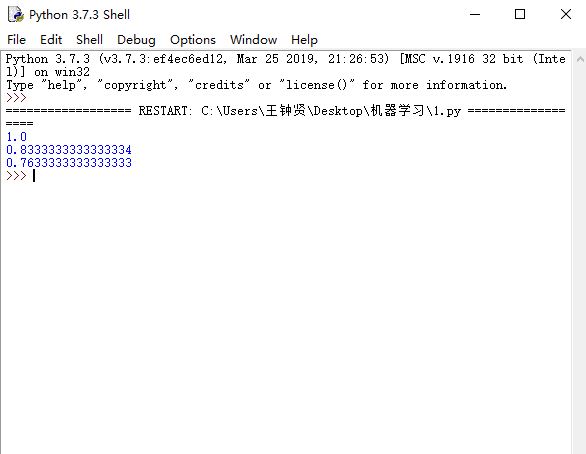
由于时间和能力有限并未做可视化
第三题的结果较好,基本上准确率为100%,第四题的白化处理没有能够完成,在网上搜索到了非方阵的白化方法,但是在做奇异值分解时,由于svd函数返回的sigam把0省略了,然后便不知道怎么操作了,第五题准确率大约在85%,也还不错,第六题在做贝叶斯分类时,出于简化计算的目的,我取了iris中花萼的长宽之和比全部的花萼长宽之和的平均大或小作为一个特征,另一特殊则为花瓣的长宽之和比全部的花萼长宽之和的平均大或小,特征可以分为4种情况,由于出现除数为0的情况,在算后验概率是除数加了0.001,更正后分类正确率在略高于70%感觉还是可以的