2017第八届蓝桥杯大赛个人赛省赛（软件类）真题 C大学A组

分析：数据比较小，可以用dfs，但是用这个方法怪难受的，重复步骤太多了
考虑先找到边界上能出边界的点集E，将所有的边反向，E能走到的点即为能走出边界的点

分析：又是一道搜索题，用string来表示出每个状态，记录每个状态的0点，深搜四种跳法，环状取模就好


分析：很明显的一道递归题
考虑当前位置分别放啊a，b，c
f(a-1,b,c,n-1)+f(a,b-1,c,n-1)+f(a,b,c-1,n-1)

还是一道搜索题，但是特别的是这次这个搜索不好搜。既然格子不好搜，那我们就搜两个图形的边界，边界必定过中心点

#include<bits/stdc++.h>
using namespace std;

int X[] = {0, -1, 1, 0, 0};
int Y[] = {0, 0, 0, -1, 1};

bool vis[10][10];
int res = 0;

void dfs(int x, int y){
  if(x == 0 || y == 0 || x == 6 || y == 6){
    res++;
    return ;
  }
  for(int i = 1 ; i <= 4 ; i++){ //上下左右四个方向
    x += X[i]; y += Y[i]; //走一步
    if(!vis[x][y]){ // 若该点未访问则继续深搜
      vis[x][y] = true; // 当前的点标注为已访问
      vis[6 - x][6 - y] = true;
      dfs(x, y); // 继续深搜
      vis[6 - x][6 - y] = false;
      vis[x][y] = false;
    }
    x -= X[i]; y -= Y[i];
  }
}

int main(){
  vis[3][3] = true;
  dfs(3, 3);
  cout << res / 4 << endl;
  return 0;
}

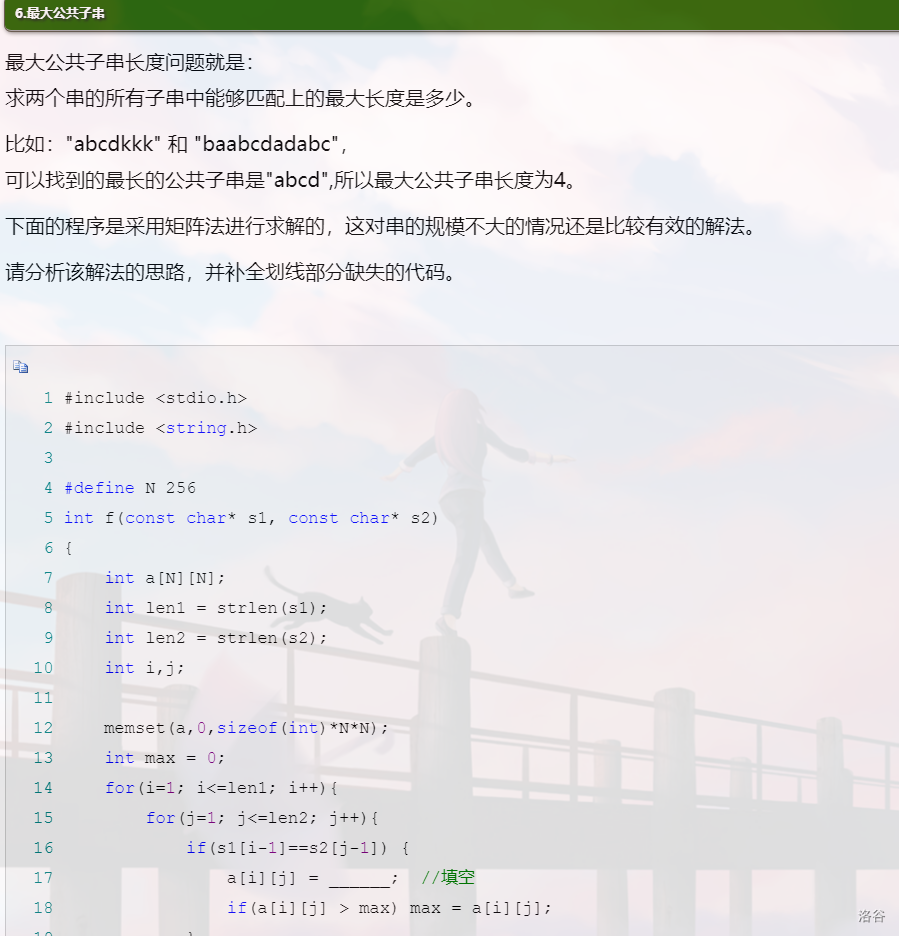
分析：就是一道模板题

首先看看结论

也就是说n个数互质的话，一定是能满足的
如果n个数不互质，就是INF
剩下的就是一个完全背包

就是一道简单的二分题目