看题

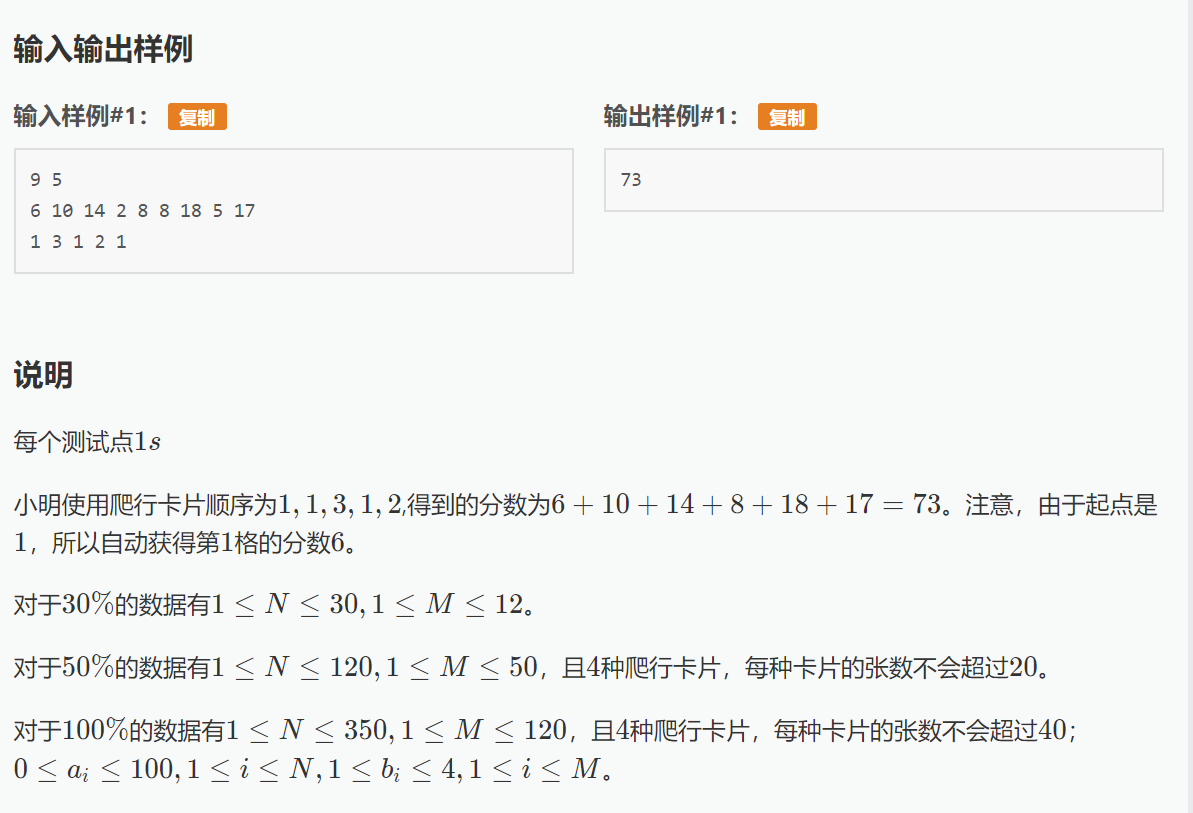
这显然是一道线性的dp
如何设计状态呢?
看看题目,总共只有4张牌,而且每张牌的个数不超过40
于是状态就很好设计了
方程如下
dp[i][j][k][l]=max(dp[i-1][j][k][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]);
dp[i][j][k][l]=max(dp[i][j-1][k][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]);
dp[i][j][k][l]=max(dp[i][j][k-1][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]);
dp[i][j][k][l]=max(dp[i][j][k][l-1]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]);
第一维表示用了i张1,第二维表示用了j张2,以此类推
其实是可以压维的,因为有一种牌的数量可以由其他的牌数推出
但是我没有写,因为这题已经够了
代码很简单易懂
#include <cstdio> #include <cstdlib> #include <iostream> #include <algorithm> #include <cstring> #include <cmath> using namespace std; const int N=50; int n,m,dp[N][N][N][N],c[5],sum,x,d[1000]; int main() { scanf("%d %d",&n,&m); for(int i=0;i<n;i++) scanf("%d",&d[i]); for(int i=1;i<=m;i++) { scanf("%d",&x); c[x]++; sum++; } dp[0][0][0][0]=d[0]; for(int i=0;i<=c[1];i++) for(int j=0;j<=c[2];j++) for(int k=0;k<=c[3];k++) { for(int l=0;l<=c[4];l++) { if(i>=1) dp[i][j][k][l]=max(dp[i-1][j][k][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]); if(j>=1) dp[i][j][k][l]=max(dp[i][j-1][k][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]); if(k>=1) dp[i][j][k][l]=max(dp[i][j][k-1][l]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]); if(l>=1) dp[i][j][k][l]=max(dp[i][j][k][l-1]+d[i*1+j*2+k*3+l*4],dp[i][j][k][l]); } } printf("%d ",dp[c[1]][c[2]][c[3]][c[4]]); return 0; }