1.高速排序
交换排序有：冒泡(选择)排序和高速排序，冒泡和选择排序的时间复杂度太高，思想非常easy临时不讨论。高速排序基于一种分治的思想，逐步地使得序列有序。
#include <iostream>
#include <conio.h>
using namespace std;
int arrs[] = { 23, 65, 12, 3, 8, 76, 345, 90, 21, 75, 34, 61 };
int arrLen = sizeof(arrs) / sizeof(arrs[0]);
void quickSort(int * arrs, int left, int right){ //挖坑填坑法
int oldLeft = left;
int oldRight = right;
bool flag = true;
int baseArr = arrs[oldLeft]; // 先挑选一个基准元素
//从数组的右端開始向前找。一直找到比base小的数字为止(包含base同等数)
while (left < right){
while (left < right && arrs[right] >= baseArr){
right--;
flag = false;
}
arrs[left] = arrs[right]; //终于找到了比baseNum小的元素，要做的事情就是此元素放到base的位置
while (left < right && arrs[left] <= baseArr){ //从左端開始向后找。一直找到比base大的数字为止（包含base同等数）
left++;
flag = false;
}
arrs[right] = arrs[left]; //终于找到了比baseNum大的元素，要做的事情就是将此元素放到最后的位置
}
arrs[left] = baseArr; //最后就是把baseNum放到该left的位置，终于。我们发现left位置的左側数值部分比base小。
// left位置右側数值比base大.至此。我们完毕了第一篇排序
if (!flag){ //假设在排序的过程中，发现存在须要交换的位置，则两边可能无序，继续对基准的左右分治处理
quickSort(arrs, oldLeft, left-1);
quickSort(arrs, left+1, oldRight);
}
}
int main()
{
quickSort(arrs, 0, arrLen - 1);
for (int i = 0; i < arrLen; i++)
cout << arrs[i] << endl;
getch();
return 0;
}
2、堆排序
堆排序属于选择排序范围。选择排序主要包含：直接选择排序和堆排序。直接选择排序非常easy，与冒泡排序非常相似，但降低了交换操作的次数。在小规模时。选择排序效率是比較高的。堆排序主要用在取前N个最大（小）值时。
堆定义
堆实际上是一棵全然二叉树。其不论什么一非叶节点满足性质：
Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]（小顶堆）或者：Key[i]>=Key[2i+1]&&key>=key[2i+2]（大顶堆）
即不论什么一非叶节点的keyword不大于或者不小于其左右孩子节点的keyword。
堆排序的思想
利用大顶堆(小顶堆)堆顶记录的是最大keyword(最小keyword)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。
其基本思想为(大顶堆)：
将初始待排序keyword序列(R1,R2....Rn)构建成大顶堆。此堆为初始的无序区；
将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
因为交换后新的堆顶R[1]可能违反堆的性质。因此须要对当前无序区(R1,R2,......Rn-1)调整为新堆。然后再次将R[1]与无序区最后一个元素交换。得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断反复此过程直到有序区的元素个数为n-1。则整个排序过程完毕。
#include <iostream>
using namespace std;
int arrs[] = { 23, 65, 12, 3, 8, 76, 345, 90, 21, 75, 34, 61 };
int arrLen = sizeof(arrs) / sizeof(arrs[0]);
void adjustHeap(int * arrs, int p, int len){
int curParent = arrs[p];
int child = 2* p + 1; //左孩子
while(child < len){ //没有孩子
if(child+1<len&&arrs[child]<arrs[child+1]){
child++; //较大孩子的下标
}
if(curParent<arrs[child]){
arrs[p]=arrs[child];
//没有将curParent赋值给孩子是由于还要迭代子树，
//假设其孩子中有大的，会上移，curParent还要继续下移。
p=child;
child=2*p+1;
}
else
break;
}
arrs[p]=curParent;
}
void heapSort(int * arrs, int len){
//建立堆，从最底层的父节点開始
for(int i = arrLen /2 -1; i>=0; i--)
adjustHeap(arrs, i, arrLen);
for(int i = arrLen -1; i>=0; i--){
int maxEle = arrs[0];
arrs[0] = arrs[i];
arrs[i] = maxEle;
adjustHeap(arrs, 0, i);
}
}
int main()
{
heapSort(arrs, arrLen );
for (int i = 0; i < arrLen; i++)
cout << arrs[i] << endl;
return 0;
}
3、插入排序(直接插入。希尔。归并)
插入排序包含：直接插入排序、希尔排序、归并排序。
直接插入排序算法，将数组划分为两种，“有序数组块”和“无序数组块”，一个个从无序数组取出元素。插入到有充数组的合适位置上。即完毕排序，最大的缺点在于要对数组元素进行移动。
希尔排序
希尔排序增加了一种叫做“缩小增量排序法”的思想，增量取法为：count/2、(count/2)/2、...、1。
希尔算法实现例如以下：
#include <iostream>
using namespace std;
int arrs[] = { 23, 65, 12, 3, 8, 76, 345, 90, 21, 75, 34, 61 };
int arrLen = sizeof(arrs) / sizeof(arrs[0]);
void shellSort(int * arrs)
{
int step = arrLen / 2; //初始增量
while(step > 0)
{
//无序部分
for(int i = step; i < arrLen; i++)
{
int temp = arrs[i];
int j;
//子序列中的插入排序,这是有序部分
for(j = i-step; j>=0 && temp < arrs[j]; j=j-step)
//在找到当前元素合适位置前。元素后移
arrs[j+step]=arrs[j];
arrs[j+step]=temp;
}
step /= 2;
}
}
int main()
{
shellSort(arrs);
for (int i = 0; i < arrLen; i++)
cout << arrs[i] << endl;
return 0;
}
归并排序
归并排序是採用分治法的一个很典型的应用，它要做两件事情：
第一： “分”, 就是将数组尽可能的分，一直分到原子级别。
第二： “并”。将原子级别的数两两合并排序，最后产生结果。
至于二个有序数列合并，仅仅要比較二个数列的第一个数，谁小就先取谁安放到暂时队列中，取了后将相应数列中这个数删除。直到一个数列为空，再将还有一个数列的数据依次取出就可以。
#include <iostream>
using namespace std;
int arrs[] = { 23, 65, 12, 3, 8, 76, 345, 90, 21, 75, 34, 61 };
int arrLen = sizeof(arrs) / sizeof(arrs[0]);
int * tempArr = new int[arrLen];
void mergeArray(int * arrs, int * tempArr, int left, int middle, int right){
int i = left, j = middle ;
int m = middle + 1, n = right;
int k = 0;
while(i <= j && m <= n){
if(arrs[i] <= arrs[m])
tempArr[k++] = arrs[i++];
else
tempArr[k++] = arrs[m++];
}
while(i <= j)
tempArr[k++] = arrs[i++];
while(m <= n)
tempArr[k++] = arrs[m++];
for(i=0; i < k; i++)
arrs[left + i] = tempArr[i];
}
void mergeSort(int * arrs, int * tempArr, int left, int right){
if(left < right){
int middle = (left + right)/2;
mergeSort(arrs, tempArr, left, middle);
mergeSort(arrs, tempArr, middle + 1, right);
mergeArray(arrs, tempArr, left, middle, right);
}
}
int main()
{
mergeSort(arrs, tempArr, 0, arrLen-1);
for (int i = 0; i < arrLen; i++)
cout << arrs[i] << endl;
return 0;
}
维基百科。归并排序
归并操作（merge），也叫归并算法。指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
迭代法[编辑]
- 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
- 设定两个指针。最初位置分别为两个已经排序序列的起始位置
- 比較两个指针所指向的元素。选择相对小的元素放入到合并空间，并移动指针到下一位置
- 反复步骤3直到某一指针到达序列尾
- 将还有一序列剩下的全部元素直接拷贝到合并序列尾
递归法[编辑]
原理例如以下（如果序列共同拥有n个元素）：
- 将序列每相邻两个数字进行归并操作，形成
个序列，排序后每一个序列包括两个元素 - 将上述序列再次归并。形成
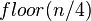个序列。每一个序列包括四个元素 - 反复步骤2，直到全部元素排序完成
int min(int x, int y)
{
return x < y ? x : y;
}
void merge_sort(int arr[], int len)
{
int* a = arr;
int* b = (int*) malloc(len * sizeof(int*));
int seg, start;
for (seg = 1; seg < len; seg += seg)
{
for (start = 0; start < len; start += seg + seg)
{
int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
int* temp = a;
a = b;
b = temp;
}
if (a != arr)
{
int i;
for (i = 0; i < len; i++)
b[i] = a[i];
b = a;
}
free(b);
}
递归版
void merge_sort_recursive(int arr[], int reg[], int start, int end)
{
if (start >= end)
return ;
int len = end - start, mid = (len >> 1) + start;
int start1 = start, end1 = mid;
int start2 = mid + 1, end2 = end;
merge_sort_recursive(arr, reg, start1, end1);
merge_sort_recursive(arr, reg, start2, end2);
int k = start;
// 将两端拍好序的区间进行归并操作
while (start1 <= end1 && start2 <= end2)
reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
while (start1 <= end1)
reg[k++] = arr[start1++];
while (start2 <= end2)
reg[k++] = arr[start2++];
for (k = start; k <= end; k++)
arr[k] = reg[k];
}
void merge_sort(int arr[], const int len)
{
int reg[len];
merge_sort_recursive(arr, reg, 0, len - 1);
}
白话经典算法系列：归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是採用分治法（Divide
and Conquer）的一个很典型的应用。
首先考虑下怎样将将二个有序数列合并。
这个很easy，仅仅要从比較二个数列的第一个数，谁小就先取谁。取了后就在相应数列中删除这个数。然后再进行比較，假设有数列为空，那直接将还有一个数列的数据依次取出就可以。
//将有序数组a[]和b[]合并到c[]中
void MemeryArray(int a[], int n, int b[], int m, int c[])
{
int i, j, k;
i = j = k = 0;
while (i < n && j < m)
{
if (a[i] < b[j])
c[k++] = a[i++];
else
c[k++] = b[j++];
}
while (i < n)
c[k++] = a[i++];
while (j < m)
c[k++] = b[j++];
}
能够看出合并有序数列的效率是比較高的，能够达到O(n)。
攻克了上面的合并有序数列问题，再来看归并排序，其的基本思路就是将数组分成二组A。B。假设这二组组内的数据都是有序的，那么就能够非常方便的将这二组数据进行排序。
怎样让这二组组内数据有序了？
能够将A，B组各自再分成二组。依次类推。当分出来的小组仅仅有一个数据时，能够觉得这个小组组内已经达到了有序，然后再合并相邻的二个小组就能够了。这样通过先递归的分解数列，再合并数列就完毕了归并排序。
//将有二个有序数列a[first...mid]和a[mid...last]合并。
void mergearray(int a[], int first, int mid, int last, int temp[])
{
int i = first, j = mid + 1;
int m = mid, n = last;
int k = 0;
while (i <= m && j <= n)
{
if (a[i] <= a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= m)
temp[k++] = a[i++];
while (j <= n)
temp[k++] = a[j++];
for (i = 0; i < k; i++)
a[first + i] = temp[i];
}
void mergesort(int a[], int first, int last, int temp[])
{
if (first < last)
{
int mid = (first + last) / 2;
mergesort(a, first, mid, temp); //左边有序
mergesort(a, mid + 1, last, temp); //右边有序
mergearray(a, first, mid, last, temp); //再将二个有序数列合并
}
}
bool MergeSort(int a[], int n)
{
int *p = new int[n];
if (p == NULL)
return false;
mergesort(a, 0, n - 1, p);
delete[] p; // new 申请内存空间没有delete(或者malloc后没有free)都可能会造成内存泄露
return true;
}
归并排序的效率是比較高的。设数列长为N。将数列分开成小数列一共要logN步，每步都是一个合并有序数列的过程。时间复杂度能够记为O(N)，故一共为O(N*logN)。由于归并排序每次都是在相邻的数据中进行操作。所以归并排序在O(N*logN)的几种排序方法（高速排序，归并排序。希尔排序，堆排序）也是效率比較高的。
在本人电脑上对冒泡排序。直接插入排序，归并排序及直接使用系统的qsort()进行比較（均在Release版本号下）
对20000个随机数据进行測试：
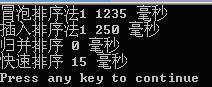
对50000个随机数据进行測试：
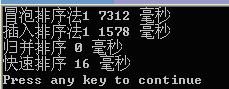
再对200000个随机数据进行測试：
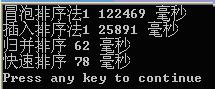
注：有的书上是在mergearray()合并有序数列时分配暂时数组。可是过多的new操作会很费时。
因此作了下小小的变化。
仅仅在MergeSort()中new一个暂时数组。后面的操作都共用这一个暂时数组。