深度学习与计算机视觉系列(5)_反向传播与它的直观理解

作者：寒小阳 && 龙心尘
时间：2015年12月。
出处：
http://blog.csdn.net/han_xiaoyang/article/details/50321873
http://blog.csdn.net/longxinchen_ml/article/details/50323183
声明：版权全部，转载请联系作者并注明出处

1. 引言

事实上一開始要讲这部分内容，我是拒绝的，原因是我觉得有一种写高数课总结的感觉。而一般直观上理解反向传播算法就是求导的一个链式法则而已。可是偏偏理解这部分和当中的细节对于神经网络的设计和调整优化又是实用的，所以硬着头皮写写吧。

问题描写叙述与动机：

• 大家都知道的。事实上我们就是在给定的图像像素向量x和相应的函数f(x)，然后我们希望能够计算f在x上的梯度(∇f(x))

• 我们之所以想解决问题，是由于在神经网络中。f相应损失函数L，而输入x则相应训练样本数据和神经网络的权重W。

  举一个特例。损失函数能够是SVM loss function。而输入则相应样本数据(xi,yi),i=1…N和权重以及bias W,b。须要注意的一点是，在我们的场景下。通常我们觉得训练数据是给定的，而权重是我们能够控制的变量。因此我们为了更新权重的等參数。使得损失函数值最小。我们一般是计算f对參数W,b的梯度。

  只是我们计算其在xi上的梯度有时候也是实用的，比方假设我们想做可视化以及了解神经网络在『做什么』的时候。

2.高数梯度/偏导基础

好了，如今開始复习高数课了，从最简单的样例開始。假如f(x,y)=xy。那我们能够求这个函数对x和y的偏导。例如以下：

f(x,y)=xy→∂f∂x=y∂f∂y=x

2.1 解释

我们知道偏导数实际表示的含义：一个函数在给定变量所在维度，当前点附近的一个变化率。也就是：

df(x)dx=limh →0f(x+h)−f(x)h

以上公式中的ddx作用在f上，表示对x求偏导数，表示的是x维度上当前点位置周边非常小区域的变化率。举个样例。假设x=4,y=−3，而f(x,y)=−12，那么x上的偏导∂f∂x=−3，这告诉我们假设这个变量(x)增大一个非常小的量。那么整个表达式会以3倍这个量减小。

我们把上面的公式变变形。能够这么看:f(x+h)=f(x)+hdf(x)dx。同理，由于∂f∂y=4，我们将y的值添加一个非常小的量h。则整个表达式变化4h。

每一个维度/变量上的偏导。表示整个函数表达式，在这个值上的『敏感度』

哦。对，我们说的梯度∇f事实上是一个偏导组成的向量，比方我们有∇f=[∂f∂x,∂f∂y]=[y,x]。即使严格意义上来说梯度是一个向量，可是大多数情况下，我们还是习惯直呼『x上的梯度』，而不是『x上的偏导』

大家都知道加法操作上的偏导数是这种：

f(x,y)=x+y→∂f∂x=1∂f∂y=1

而对于一些别的操作，比方max函数，偏导数是这种(后面的括号表示在这个条件下)：

f(x,y)=max(x,y)→∂f∂x=1(x>=y)∂f∂y=1(y>=x)

3. 复杂函数偏导的链式法则

考虑一个麻烦一点的函数，比方f(x,y,z)=(x+y)z。当然。这个表达式事实上还没那么复杂。也能够直接求偏导。可是我们用一个非直接的思路去求解一下偏导。以帮助我们直观理解反向传播中。假设我们用换元法，把原函数拆成两个部分q=x+y和f=qz。对于这两个部分，我们知道怎么求解它们变量上的偏导：∂f∂q=z,∂f∂z=q ∂q∂x=1,∂q∂y=1，当然q是我们自己设定的一个变量。我们对他的偏导全然不感兴趣。
那『链式法则』告诉我们一个对上述偏导公式『串联』的方式，得到我们感兴趣的偏导数:∂f∂x=∂f∂q∂q∂x

看个样例：

x = -2; y = 5; z = -4

# 前向计算
q = x + y # q becomes 3
f = q * z # f becomes -12

# 类反向传播:
# 先算到了 f = q * z
dfdz = q # df/dz = q
dfdq = z # df/dq = z
# 再算到了 q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1 恩，链式法则
dfdy = 1.0 * dfdq # dq/dy = 1

链式法则的结果是，仅仅剩下我们感兴趣的[dfdx,dfdy,dfdz]，也就是原函数在x,y,z上的偏导。

这是一个简单的样例，之后的程序里面我们为了简洁，不会完整写出dfdq，而是用dq取代。

以下是这个计算的示意图：

4. 反向传播的直观理解

一句话概括：反向传播的过程。实际上是一个由局部到全部的精妙过程。比方上面的电路图中，事实上每一个『门』在拿到输入之后，都能计算2个东西：

• 输出值
• 相应输入和输出的局部梯度

并且非常明显。每一个门在进行这个计算的时候是全然独立的。不须要对电路图中其它的结构有了解。然而，在整个前向传输过程结束之后，在反向传播过程中，每一个门却能逐步累积计算出它在整个电路输出上的梯度。『链式法则』告诉我们每一个门接收到后向传来的梯度。同一时候用它乘以自己算出的对每一个输入的局部梯度，接着往后传。

以上面的图为例。来解释一下这个过程。加法门接收到输入[-2, 5]同一时候输出结果3。

由于加法操作对两个输入的偏导都应该是1。电路兴许的部分算出终于结果-12。在反向传播过程中，链式法则是这样做的：加法操作的输出3。在最后的乘法操作中，获得的梯度为-4，假设把整个网络拟人化，我们能够觉得这代表着网络『想要』加法操作的结果小一点，并且是以4*的强度来减小。加法操作的门获得这个梯度-4以后。把它分别乘以本地的两个梯度(加法的偏导都是1)，1*-4=-4。假设输入x减小，那加法门的输出也会减小，这样乘法输出会相应的添加。

反向传播，能够看做网络中门与门之间的『关联对话』，它们『想要』自己的输出更大还是更小(以多大的幅度)，从而让最后的输出结果更大。

5. Sigmoid样例

上面举的样例事实上在实际应用中非常少见。我们非常多时候见到的网络和门函数更复杂。可是不论它是什么样的。反向传播都是能够使用的，唯一的差别就是可能网络拆解出来的门函数布局更复杂一些。

我们以之前的逻辑回归为例：

f(w,x)=11+e−(w0x0+w1x1+w2)

这个看似复杂的函数。事实上能够看做一些基础函数的组合，这些基础函数及他们的偏导例如以下：

f(x)=1x→dfdx=−1/x2fc(x)=c+x→dfdx=1f(x)=ex→dfdx=exfa(x)=ax→dfdx=a

上述每一个基础函数都能够看做一个门，如此简单的初等函数组合在一块儿却能够完毕逻辑回归中映射函数的复杂功能。以下我们画出神经网络，并给出详细输入输出和參数的数值：

这个图中，[x0, x1]是输入，[w0, w1,w2]为可调參数，所以它做的事情是对输入做了一个线性计算(x和w的内积)。同一时候把结果放入sigmoid函数中，从而映射到(0,1)之间的数。

上面的样例中，w与x之间的内积分解为一长串的小函数连接完毕，而后接的是sigmoid函数σ(x)，有趣的是sigmoid函数看似复杂。求解倒是的时候却是有技巧的，例如以下：

σ(x)=11+e−x→dσ(x)dx=e−x(1+e−x)2=(1+e−x−11+e−x)(11+e−x)=(1−σ(x))σ(x)

你看。它的导数能够用自己非常easy的又一次表示出来。所以在计算导数的时候非常方便。比方sigmoid函数接收到的输入是1.0。输出结果是-0.73。那么我们能够非常方便地计算得到它的偏导为(1-0.73)*0.73~=0.2。我们看看在这个sigmoid函数部分反向传播的计算代码：

w = [2,-3,-3] # 我们随机给定一组权重
x = [-1, -2]

# 前向传播
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid函数

# 反向传播经过该sigmoid神经元
ddot = (1 - f) * f # sigmoid函数偏导
dx = [w[0] * ddot, w[1] * ddot] # 在x这条路径上的反向传播
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 在w这条路径上的反向传播
# yes！就酱紫算完了。是不是非常easy？

5.1 project实现小提示

回过头看看上头的代码。你会发现，实际写代码实现的时候，有一个技巧能帮助我们非常easy地实现反向传播，我们会把前向传播的过程分解成反向传播非常easy追溯回来的部分。

6. 反向传播实战：复杂函数

我们看一个稍复杂一些的函数：

f(x,y)=x+σ(y)σ(x)+(x+y)2

额，插一句。这个函数没有不论什么实际的意义。我们提到它。仅仅是想举个样例来说明复杂函数的反向传播怎么使用。

假设直接对这个函数求x或者y的偏导的话，你会得到一个非常复杂的形式。可是假设你用反向传播去求解详细的梯度值的话。却全然没有这个烦恼。我们把这个函数分解成小部分，进行前向和反向传播计算，就可以得到结果。前向传播计算的代码例如以下：

x = 3 # 样例
y = -4

# 前向传播
sigy = 1.0 / (1 + math.exp(-y)) # 单值上的sigmoid函数
num = x + sigy 
sigx = 1.0 / (1 + math.exp(-x)) 
xpy = x + y      
xpysqr = xpy**2                 
den = sigx + xpysqr
invden = 1.0 / den                                       
f = num * invden # 完毕！                                

注意到我们并没有一次性把前向传播最后结果算出来，而是刻意留出了非常多中间变量。它们都是我们能够直接求解局部梯度的简单表达式。因此，计算反向传播就变得简单了：我们从最后结果往前看，前向运算中的每一个中间变量sigy, num, sigx, xpy, xpysqr, den, invden我们都会用到，仅仅只是后向传回的偏导值乘以它们。得到反向传播的偏导值。

反向传播计算的代码例如以下：

# 局部函数表达式为 f = num * invden
dnum = invden                              
dinvden = num    
# 局部函数表达式为 invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                            
# 局部函数表达式为 den = sigx + xpysqr
dsigx = (1) * dden
dxpysqr = (1) * dden
# 局部函数表达式为 xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# 局部函数表达式为 xpy = x + y
dx = (1) * dxpy                                                   
dy = (1) * dxpy                                                   
# 局部函数表达式为 sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # 注意到这里用的是 += !!
# 局部函数表达式为 num = x + sigy
dx += (1) * dnum                                                  
dsigy = (1) * dnum                                                
# 局部函数表达式为 sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 
# 完事！

实际编程实现的时候，须要注意一下：

• 前向传播计算的时候注意保留部分中间变量：在反向传播计算的时候，会再次用到前向传播计算中的部分结果。这在反向传播计算的回溯时可大大加速。

6.1 反向传播计算中的常见模式

即使由于搭建的神经网络结构形式和使用的神经元都不同。可是大多数情况下，后向计算中的梯度计算能够归到几种常见的模式上。比方，最常见的三种简单运算门(加、乘、最大)。他们在反向传播运算中的作用是非常easy和直接的。

我们一起看看以下这个简单的神经网：

上图里有我们提到的三种门add,max和multiply。

• 加运算门在反向传播运算中，无论输入值是多少，取得它output传回的梯度(gradient)然后均匀地分给两条输入路径。由于加法运算的偏导都是+1.0。
• max(取最大)门不像加法门，在反向传播计算中，它仅仅会把传回的梯度回传给一条输入路径。由于max(x,y)仅仅对x和y中较大的那个数。偏导为+1.0，而还有一个数上的偏导是0。
• 乘法门就更好理解了，由于x*y对x的偏导为y，而对y的偏导为x。因此在上图中x的梯度是-8.0。即-4.0*2.0

由于梯度回传的原因，神经网络对输入非常敏感。

我们拿乘法门来举例。假设输入的xi全都变成原来1000倍，而权重w不变，那么在反向传播计算的时候。x路径上获得的回传梯度不变，而w上的梯度则会变大1000倍，这使得你不得不减少学习速率(learning rate)成原来的1/1000以维持平衡。因此在非常多神经网络的问题中，输入数据的预处理也是非常重要的。

6.2 向量化的梯度运算

上面全部的部分都是在单变量的函数上做的处理和运算，实际我们在处理非常多数据(比方图像数据)的时候，维度都比較高。这时候我们就须要把单变量的函数反向传播扩展到向量化的梯度运算上。须要特别注意的是矩阵运算的每一个矩阵维度，以及转置操作。

我们通过简单的矩阵运算来拓展前向和反向传播运算。演示样例代码例如以下：

# 前向传播运算
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)

# 假如我们如今已经拿到了回传到D上的梯度dD
dD = np.random.randn(*D.shape) # 和D同维度
dW = dD.dot(X.T) #.T 操作计算转置， dW为W路径上的梯度
dX = W.T.dot(dD)  #dX为X路径上的梯度

7. 总结

直观地理解。反向传播能够看做图解求导的链式法则。
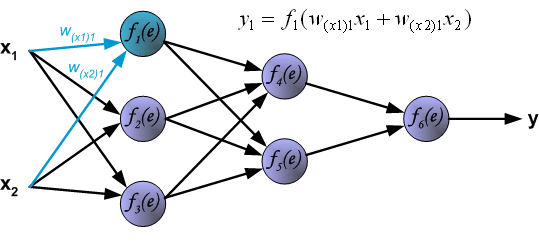
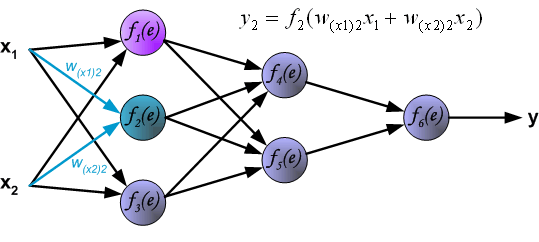
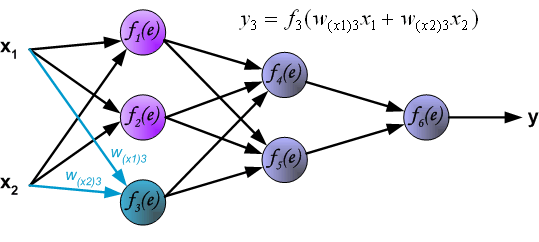
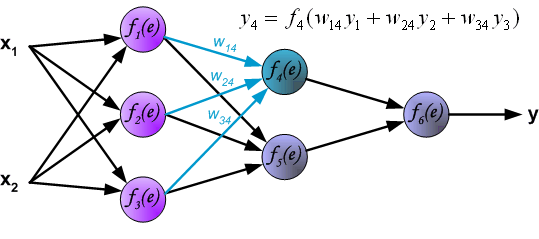
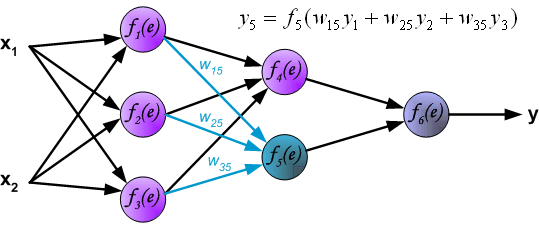
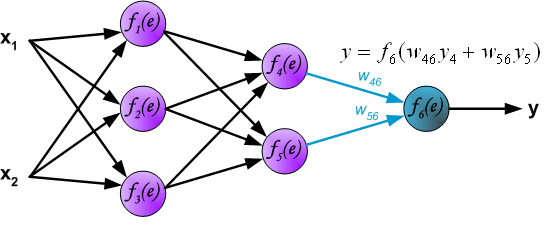
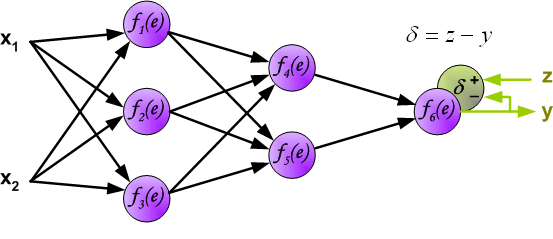
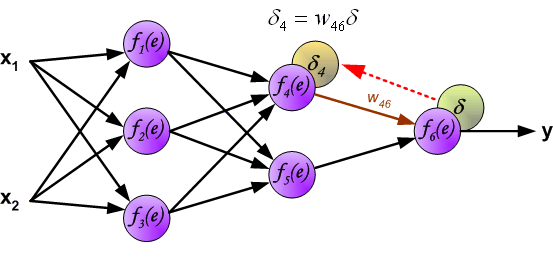
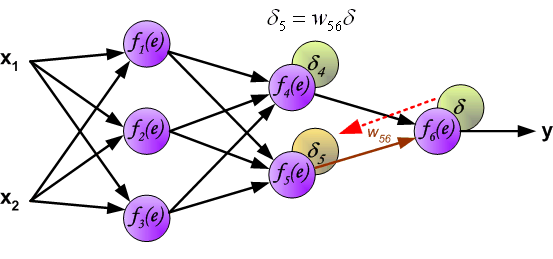
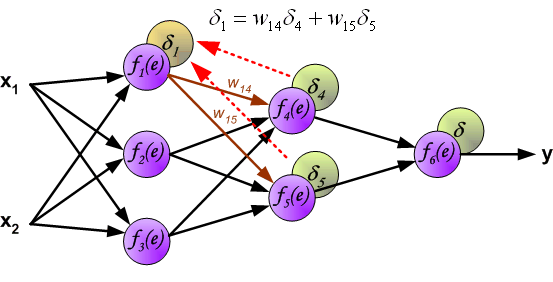
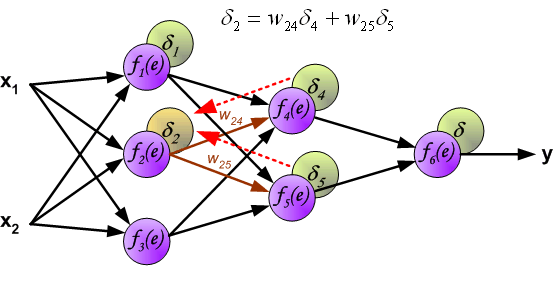
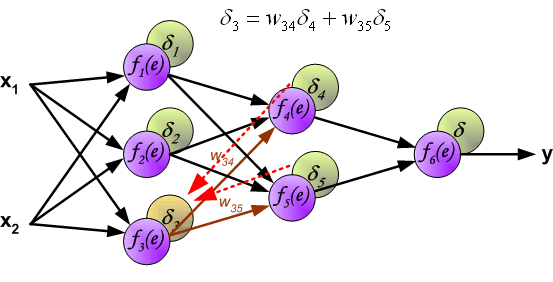
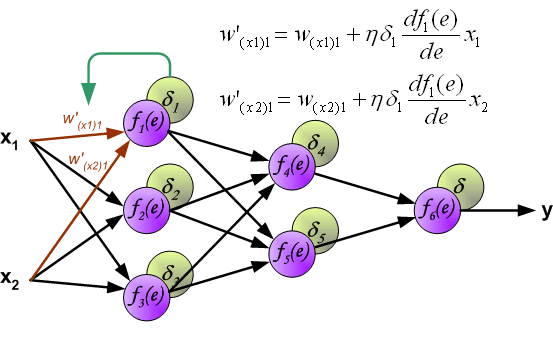
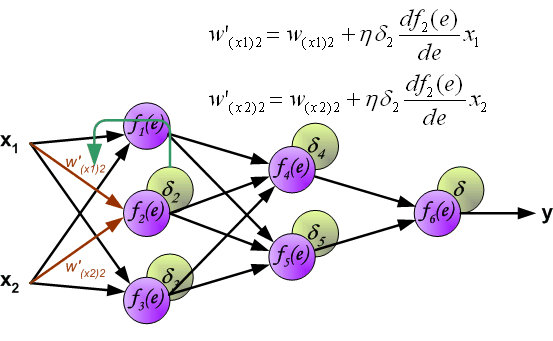
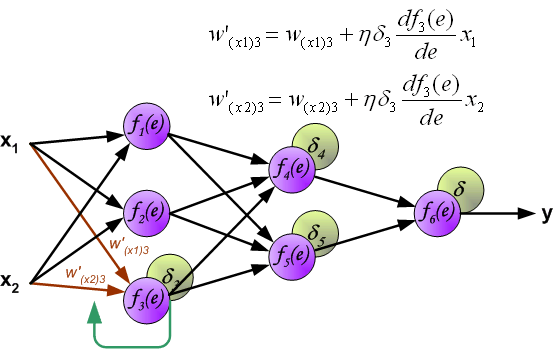
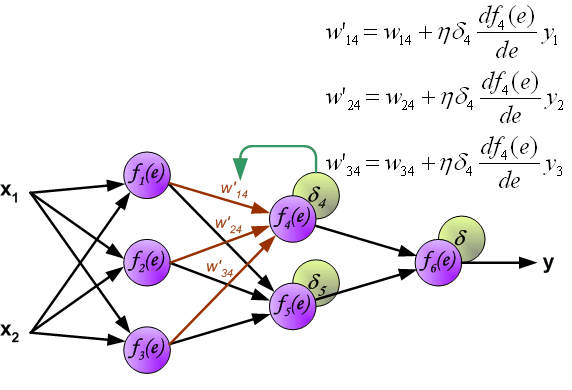
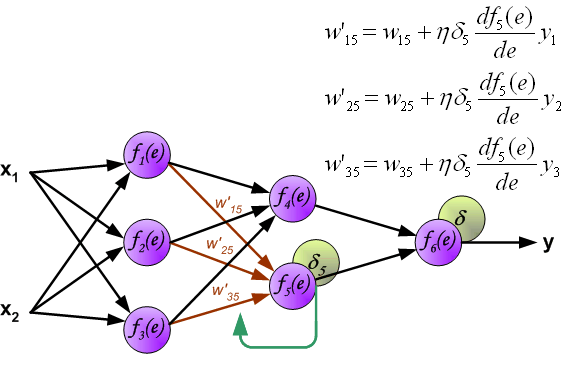
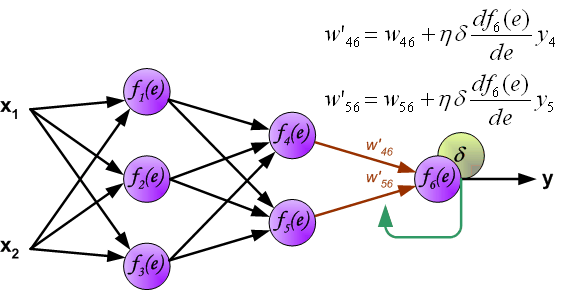
最后我们用一组图来说明实际优化过程中的正向传播与反向残差传播：

參考资料与原文

cs231n 反向传播与直观理解