题目传送门
题目描述
为了从F个草场中的一个走到另一个,贝茜和她的同伴们有时不得不路过一些她们讨厌的可怕的树.奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径.给出所有R条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量, 路径由若干道路首尾相连而成.两条路径相互分离,是指两条路径没有一条重合的道路.但是,两条分离的路径上可以有一些相同的草场. 对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
输入格式
第1行输入F和R,接下来R行,每行输入两个整数,表示两个草场,它们之间有一条道路。
输出格式
最少的需要新建的道路数。
样例
样例输入:
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
样例输出:
2
数据范围与提示
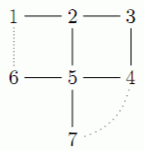
图中实线表示已有的道路,虚线表示新建的两条道路。
现在可以检验一些路径,比如:
草场1和草场2:1→2和1→6→5→2。
草场1和草场4:1→2→3→4和1→6→5→4。
草场3和草场7:3→4→7和3→2→5→7。
事实上,每一对草场之间都连接了两条分离的路径。
1≤F≤5000,F-1≤R≤10000。
注意会有重边!!!
题解
看到这道题,马上想到了塔尖,缩e-DCC。
然后答案即为得到的$frac{这棵树上的叶子节点的个数+1}{2}$,利用性质,连边为1的点即为叶子节点,统计答案即可。
代码细节较多,建议尝试自己根据自己的理解手打。
当然也有大神缩v-DCC,直接A掉。
还有这么一种解法,塔尖之后不用重新建图,而是直接判断在一条边两端的点low的值是否相同,如果不同那么就让度数+1。(他们的塔尖通过在一开始直接判断e.to是否等于father,如果相等直接continue)。
但是这样并不正确!!!
考虑这道题会有重边,所以如果low[x]≠low[y],但是它们还可能属于一个强联通分量。
不过如果你使用了可以规避重边的方法,那么就没有问题。
综上所述,板子要理解,并能灵活运用!!!
代码时刻
e-DCC
#include<bits/stdc++.h>
using namespace std;
struct rec
{
int from;
int nxt;
int to;
}e[200010],wzc[200010];
int head[5010],cnt=1;
int headw[5010],cntw=1;
int F,R;
int dfn[5010],low[5010],tot;
bool bridge[200010];
int c[5010],dcc;
int ans[5010];
int sum;
bool vis[5010];
void add(int x,int y)
{
e[++cnt].nxt=head[x];
e[cnt].from=x;
e[cnt].to=y;
head[x]=cnt;
}
void tarjan(int x,int in_edge)//判断桥
{
dfn[x]=low[x]=++tot;
for(int i=head[x];i;i=e[i].nxt)
{
if(!dfn[e[i].to])
{
tarjan(e[i].to,i);
low[x]=min(low[x],low[e[i].to]);
if(dfn[x]<low[e[i].to])
bridge[i]=bridge[i^1]=1;
}
else if(i!=(in_edge^1))
low[x]=min(low[x],dfn[e[i].to]);
}
}
void dfs(int x)//求e-DCC
{
c[x]=dcc;
for(int i=head[x];i;i=e[i].nxt)
{
if(c[e[i].to]||bridge[i])continue;
dfs(e[i].to);
}
}
int main()
{
scanf("%d%d",&F,&R);
for(int i=1;i<=R;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
for(int i=1;i<=F;i++)
if(!dfn[i])tarjan(i,0);
for(int i=1;i<=F;i++)
if(!c[i])
{
++dcc;
dfs(i);
}
for(int i=2;i<=cnt;i++)//开始计算答案
if(c[e[i].from]!=c[e[i].to])ans[c[e[i].from]]++;
for(int i=1;i<=dcc;i++)
if(ans[i]==1)sum++;
printf("%d",(sum+1)/2);
return 0;
}
v-DCC
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
int const maxn=5010;
struct node{int st,to,nxt;}l[4*maxn];
vector<int>v[maxn];
int n,m,head[maxn],tot,num,in[maxn*2],ans;
int dfn[maxn],low[maxn],stack[maxn],bl[maxn*2],id[maxn*2],cut[maxn*2],top,now,cnt,rt;
void add1(int x,int y)
{
l[++tot].to=y;
l[tot].st=x;
l[tot].nxt=head[x];
head[x]=tot;
}
void tarjan(int x)//割点
{
dfn[x]=low[x]=++now,stack[++top]=x;
if(x==rt&&head[x]==0)
{
v[++cnt].push_back(x);
bl[x]=cnt;
return ;
}
int flag=0;
for(int i=head[x];i;i=l[i].nxt)
{
int y=l[i].to;
if(!dfn[y])
{
tarjan(y);
low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x])
{
flag++;
if(x!=rt||flag>1) cut[x]=1;
cnt++;int z;
do{
z=stack[top--];
v[cnt].push_back(z);
bl[z]=cnt;
}while(y!=z);
v[cnt].push_back(x);
}
}
else low[x]=min(low[x],dfn[y]);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<=m;i++)
{
scanf("%d%d",&x,&y);
add1(x,y),add1(y,x);
}
for(int i=1;i<=n;i++) if(!dfn[i]) rt=i,tarjan(i);
num=cnt;
for(int i=1;i<=n;i++) if(cut[i]) id[i]=++num;
for(int i=1;i<=cnt;i++)
for(int j=0;j<v[i].size();j++)
if(cut[v[i][j]]) in[i]++;
for(int i=1;i<=cnt;i++) if(in[i]==1) ans++;
printf("%d",(ans+1)/2);
return 0;
}
rp++