一、概念
逻辑回归一般用于解决二分类的问题。即结果为（0或1）的预测。也可以用于多分类。
二、举例
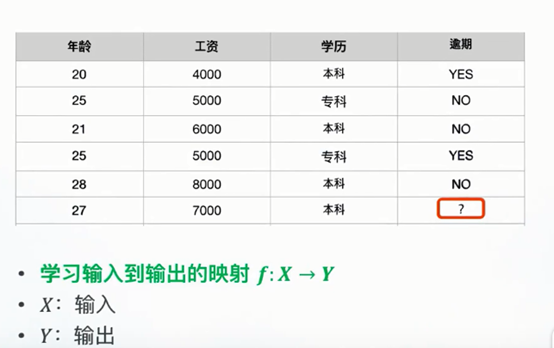
我们将X（年龄，工资，学历） 作为输入，通过上边数据的学习，来判断最后一个人逾期的概率。
这时，可以定义一个条件概率公式P（Y | X）
根据这个公式我们可以尝试将第一条数据表示出来P（Y=1|（20,4000，本科））
这样通过学习已有数据，就可以进行预测，计算P（Y=1|（27,7000，本科）） ，如果结果大于0.5则说明大概率结果为逾期，否则反之。
三、
我们尝试用线性回归表示 P（Y|X）= 。但是从概率的角度我们不难发现，这样的表示方法的值域范围为 （-∞，+∞）的，明显与概率需要（0,1）不同，所以这个不能表示概率。
所以这时候可以使用逻辑函数，这个函数的表示为：
图像如下：
所以，结合上文的内容，我们可以得到新的条件概率公式
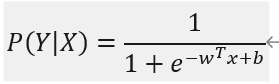
这个公式中w为一个向量，x为条件，b为调和用的常数。
因为主要针对的是二分类的问题，根据上述公式容易得出
这两个公式合并为
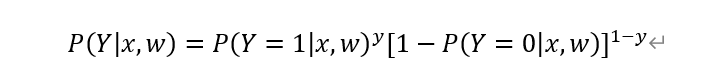
通过带入y=1或者y=0发现结果均符合上式。
四、逻辑回归是线性分类器
针对一模型是线性分类器或者是非线性分类器的依据是根据决策边界来确定的。
决策边界：
画一个粗糙的图进行说明
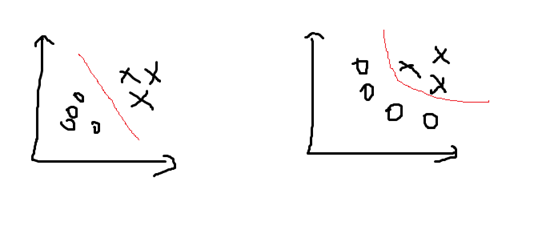
图中的红线即表示不同模型下的分类边界，这个线是通过计算结果P=0.5的结果连成的一条线，左边的即为线性的，右边为非线性的。
计算决策边界的方程式的计算可以根据下式
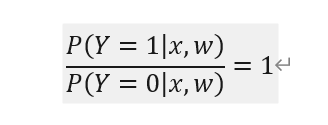
将①②式代入之后得出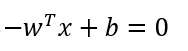 
，这个式子就是逻辑回归的决策边界。
其他函数的决策边界也是这样计算。
五、计算x，w
如果想要计算x，w。需要一个函数，来求这两个值的最大值。
找到让右边最大的时候，w，b的值。
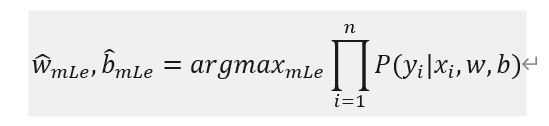
关于这个式子的计算，可以在连乘符号前边加上log 函数。（因为log严格递增，在最值上对结果不产生影响。而且经过多次连乘，计算机可能无法精确计算，换成log比较方便。）
取完log之后，在前边加上一个 负号，即找最小值即可。
公式如下：
(将三中的式子代入)
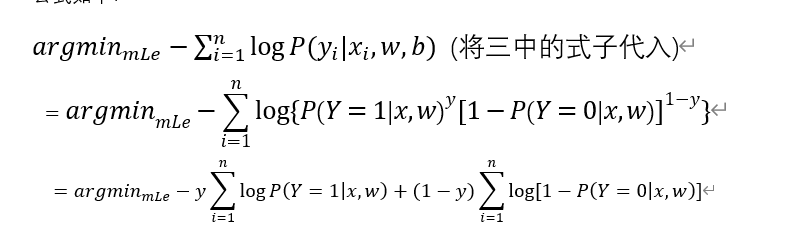
将P概率部分规定为逻辑函数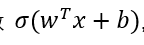
,代入之后使用极大似然估计法求解。
极大似然估计法就是把这个函数分别对w，b 求偏导得到两个式子。分别记为
接下来使用梯度下降法来求即可。
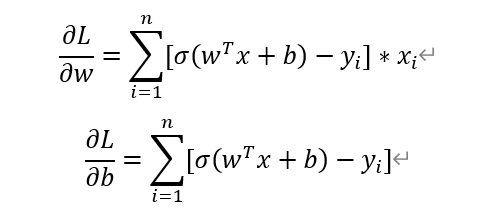
六、梯度下降法
如果想要求一个函数f（x）的最小值的参数x，最好的情况下这个函数是凹函数，这样存在极小值点，找到记为最小值。但是，假如这个函数分段是凹函数，这样就可能存在多个极值点，并不一定能确定究竟是那个，或者有多少个结果。所以使用梯度下降法求解比较合适。
求f（w）最小时的参数w
初始化w1, t的取值范围是1,2,3…….
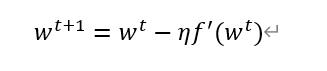
（参数说明，）η为步长，步长的设定要合适，太长找不到结果，太短则会走很多弯路。在计算过程中η可变。
这样通过多次计算w即可收敛，趋近于一个数。
至于这个计算多少次可以结束一般有以下几种选择：
-
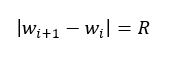（R为规定的一个阈值） - 如果w一直递减，出现递增的时候停止。同理，如果一直递增，出现递减的时候停止
- 设定一个次数例如1000次，一个函数在经过若干次计算一定会收敛，我们设定的次数大于这个数即可，只是会产生一些不必要的计算。
七、逻辑回归的梯度下降法
初始化 t=1,2,3,,,,,,,
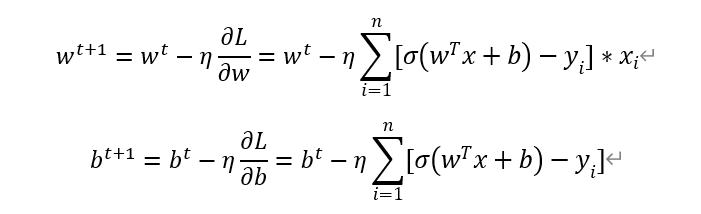
这样逻辑回归的梯度下降法基本完成了。
八、思考
1.上述方法有一点缺点就是，每次计算加上新的样本都要重新计算，这样使得当训练数据很大的时候运算量就很大。
2.有一种方法是打乱数据，每次使用一个，相当于求和函数去掉。
3.第二种方式样本量偏少，所以还有一种方式是选取一小部分数据作为训练样本来进行求和，这样可能稍微好一点。