力扣算法：N 皇后

原题链接：https://leetcode-cn.com/problems/n-queens

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

 

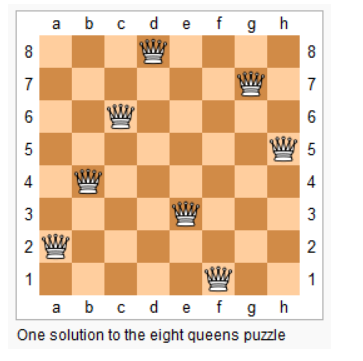
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

解题思路：

首先这是经典的皇后问题，所以采用回溯法的方法。我们需要使用三个集合来记录不能放皇后的列或者斜线，所以需要找规律。

当是左斜线的时候，行下标-列下表 = 定值说明在同一左斜线上

当是右斜线的时候，行下标+列下表=定值 说明在同一右斜线上

使用数组 queens 来记录 queens[i]  =p  ,表示第i行的皇后放在下标 p 的位置。

之后在很剧queens数组来确定list结果。并放入最终的结果集。

代码如下：

public List<List<String>> solveNQueens(int n) {
        //结果集
        List<List<String>> result = new ArrayList<List<String>>();

        //存放皇后所在的列
        int[] queens = new int[n];
        //三个结果集，分别存储失效的列，左斜线，右斜线
        Set<Integer> lie = new HashSet<Integer>();
        Set<Integer> zuoXie = new HashSet<Integer>(); //行下标-列下表 固定
        Set<Integer> youXie = new HashSet<Integer>();//行下标+列下表 固定
        backtrack(result,queens,n,0,lie,zuoXie,youXie);


        return result;
    }

    public void backtrack(List<List<String>> result,int[] queens,int n,int row,Set<Integer> lie,Set<Integer> zuoXie,Set<Integer> youXie){
        if(row==n){
            //填充完成
            List<String> list=getResult(queens,n);
            result.add(list);
        }else {
            //在第 row 行上，从左到右按顺序排查
            for(int i=0;i<n;i++){
                //排查列
                if(lie.contains(i))
                    continue;
                //排查左斜线
                if(zuoXie.contains(row-i)){
                    continue;
                }
                if (youXie.contains(row+i)) {
                    continue;
                }
                //到达这一步说明i点可以存放。
                queens[row]=i;
                lie.add(i);
                zuoXie.add(row-i);
                youXie.add(row+i);
                //递归
                backtrack(result,queens,n,row+1,lie,zuoXie,youXie);
                //到达这一步说明有问题，需要回溯
                queens[row]=-1;
                lie.remove(i);
                zuoXie.remove(row-i);
                youXie.remove(row+i);
            }
        }

    }

    //将queens数组的结果转化为List数组类型
    public List<String> getResult(int[] queens,int n){
        List<String> list = new ArrayList<>() ;
        for (int i=0;i<n;i++){
            char[] rows=new char[n];
            for(int j=0;j<n;j++)
                rows[j]='.';
            rows[queens[i]]='Q';
            list.add(new String(rows));
        }
        return list;
    }