随机块模型是随机图的生成模型,用于生成图结构。该模型针对无向无权网络有以下两个假设:
- 每个节点都会有且仅有一个社团归属
- 每条边的生成只与两个节点所在的社团有关
- 网络中社团个数固定为K
模型认为对于一个节点,我们要先确定节点的社团归属,确定好后再确定其与自己所在社团以及其他社团内的节点之间的连边关系。
因此我们有静态网络随机块模型的概率图模型:
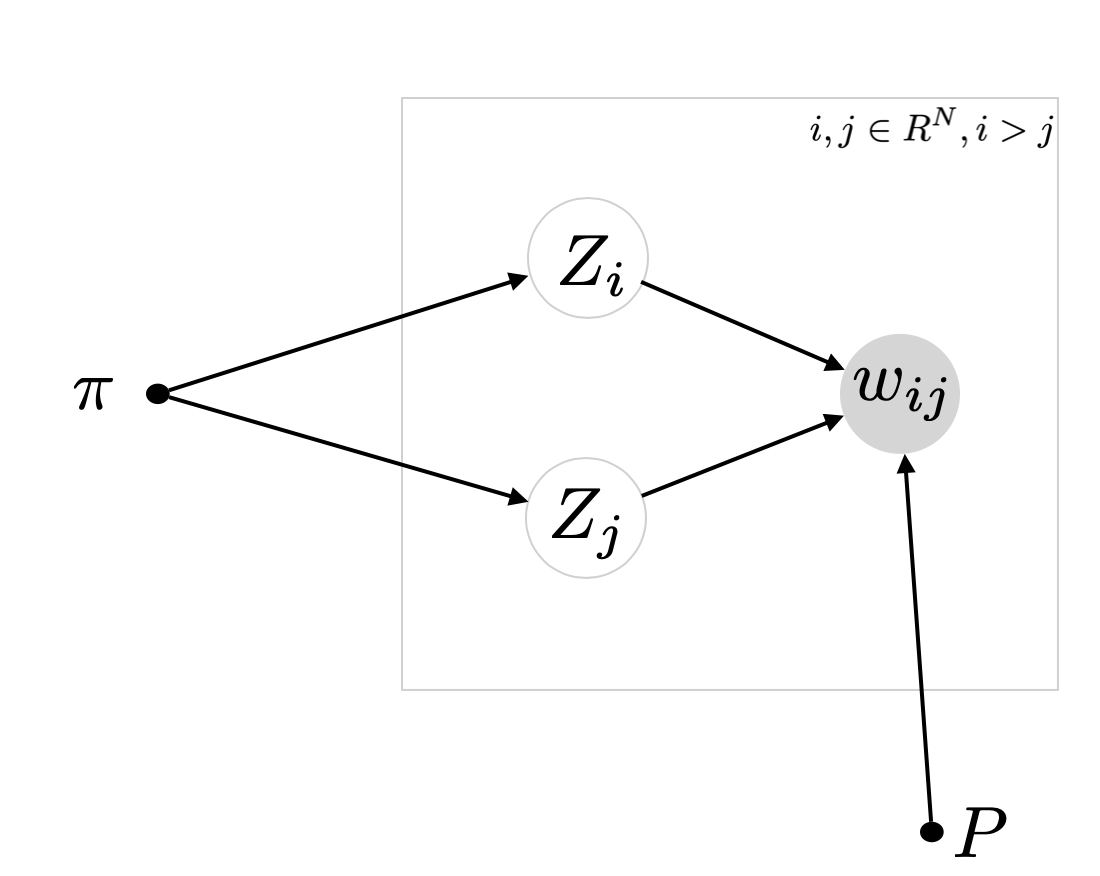
其中π是长度为K的向量,P为K*K的矩阵,Z代表节点的社团归属,可以是社团编号,也可以是一条one-hot的向量。而W代表网络的邻接矩阵。
其生成过程如下:
- 对节点i属于N:
- 以概率π划分其所属社团Zi
- 对节点对i,j:
- wij 服从Bernoulli(·|P_zi,zj)
依据以上概率图和其生成过程,就可以写出其联合概率分布。接下来我们就可以求出模型关于Z的后验并最大化后验概率得出每个节点的社团划分。