---恢复内容开始---

由题意可知,
p(a1)=0.2 ,p(a2)=0.3 ,p(a3)=0.5
可知X(ai)=i, X(a1)=1,X(a2)=2,X(a3)=3
FX(0)=0,FX(1)=0.2 ,FX(2)=0.5 ,FX(3)=1.0, U(0)=1 ,L(0)=0
根据公式,L(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn-1)
u(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn)
第1次 出现a1时
L(1)=L(0)+(U(0)-L(0))Fx(0)=0
U(1)=L(0)+(U(0)-L(0))Fx(1)=0.2
第2次出现a1时
L(2)=L(1)+(U(1)-L(1))Fx(0)=0
U(2)=L(1)+(U(1)-L(1))Fx(1)=0.04
第3次 出现a3时
L(3)=L(2)+(U(2)-L(2))Fx(2)=0.02
U(3)=L(2)+(U(2)-L(2))Fx(3)=0.04
第4次 出现a2时
L(4)=L(3)+(U(3)-L(3))Fx(1)=0.024
U(4)=L(3)+(U(3)-L(3))Fx(2)=0.03
第5次 出现a3时
L(5)=L(4)+(U(4)-L(4))Fx(2)=0.027
U(5)=L(4)+(U(4)-L(4))Fx(3)=0.03
第6次 出现a1时
L(6)=L(5)+(U(5)-L(5))Fx(0)=0.027
U(6)=L(5)+(U(5)-L(5))Fx(1)=0.0276
即求得序列a1a1a3a2a3a1的实值标签为:TX(113231)=(L(6)+ U(6))/2=0.0273;
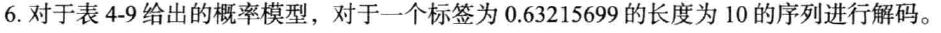
解:
由题可知:Tx=0.63215699, Fx(0)=0, Fx(1)=0.2, Fx(2)=0.5, Fx(3)=1, k>3.
将U(0)=1,L(0)=0。
且
根据公式,L(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn-1)
U(n)=L(n-1)+(U(n-1)-L(n-1))Fx(xn)
t*=(tag-L(n-1))/(U(n-1) -L(n-1))
所以:
t*=(0.63215699-0)/(1 -0)=0.63215699
Fx(2)=0.5≤t*≤1=Fx(3)
L(1) =L(0) +(U(0) -L(0) )Fx(2)=0+(1-0)*0.5=0.5
U(1) =L(0) +(U(0) -L(0) )Fx(3)=0+(1-0)*1=1
因此,得到的第1个序列为:a3
t*=(0.63215699-0.5)/(1 -0.5)=0.26431398
Fx(1)=0.2≤t*≤0.5=Fx(2)
U(2) =L(1) +(U(1) -L(1) )Fx(1)=0.5+(1-0.5)*0.2=0.6
U(2) =L(1) +(U(1) -L(1) )Fx(2)=0.5+(1-0.5)*0.5=0.75
因此,得到的第2个序列为:a2
t*=(0.63215699-0.5)/(1 -0.5)=0.26431398
Fx(1)=0.2≤t*≤0.5=Fx(2)
L(3) =L(2) +(U(2) -L(2) )Fx(1)=0.6+(0.75-0.6)*0.2=0.63
U(3) =L(2) +(U(2) -L(2) )Fx(2)=0.6+(0.75-0.6)*0.5=0.675
因此,得到的第3个序列为:a2
t*=(0.63215699-0.63)/(0.675 -0.63)=0.04793311
Fx(0)=0≤t*≤0.2=Fx(1)
L(4) =L(3) +(U(3) -L(3) )Fx(0)=0.63+(0.675-0.63)*0=0.63
U(4) =L(3) +(U(3) -L(3) )Fx(1)=0.63+(0.675-0.63)*0.2=0.639
因此,得到的第4个序列为:a1
t*=(0.63215699-0.63)/(0.639 -0.63)=0.23966556
Fx(1)=0.2≤t*≤0.5=Fx(2)
L(5) =L(4) +(U(4) -L(4) )Fx(1)=0.63+(0.639-0.63)*0.2=0.6318
U(5) =L(4) +(U(4) -L(4) )Fx(2)=0.63+(0.639-0.63)*0.5=0.6345
因此,得到的第5个序列为:a2
t*=(0.63215699-0.6318)/(0.6345 -0.6318)=0.13221852
Fx(0)=0≤t*≤0.2=Fx(1)
L(6) =L(5) +(U(5) -L(5) )Fx(0)=0.6318+(0.6345-0.6318)*0=0.6318
U(6) =L(5) +(U(5) -L(5) )Fx(1)=0.6318+(0.6345-0.6318)*0.2=0.63234
因此,得到的第6个序列为:a1
t*=(0.63215699-0.6318)/(0.63234 -0.6318)=0.66109259
Fx(2)=0.5≤t*≤1=Fx(3)
L(7) =L(6) +(U(6) -L(6) )Fx(2)=0.6318+(0.63234-0.6318)*0.5=0.63207
U(7) =L(6) +(U(6) -L(6) )Fx(3)=0.6318+(0.63234-0.6318)*1=0.63234
因此,得到的第7个序列为:a3
t*=(0.63215699-0.63207)/(0.63234 -0.63207)=0.66109259
Fx(1)=0.2≤t*≤0.5=Fx(2)
L(8) =L(7) +(U(7) -L(7) )Fx(1)=0.63207+(0.63234-0.63207)*0.2=0.632124
U(8) =L(7) +(U(7) -L(7) )Fx(2)=0.63207+(0.63234-0.63207)*0.5=0.632205
因此,得到的第8个序列为:a2
t*=(0.63215699-0.63207)/(0.63234 -0.63207)=0.66109259
Fx(1)=0.2≤t*≤0.5=Fx(2)
L(9) =L(8) +(U(8) -L0(8) )Fx(1)=0.632124+(0.632205-0.632124)*0.2=0.6321402
U(9) =L(8) +(U(8) -L(8) )Fx(2)=0.632124+(0.632205-0.632124)*0.5=0.6321645
因此,得到的第9个序列为:a2
t*=(0.63215699-0.6321402)/(0.6321645 -0.6321402)=0.69835391
Fx(2)=0.5≤t*≤1=Fx(3)
因此,得到的第10个序列为:a3
所以,序列为a3a2a2a1a2a1a3a2a2a3。