多视图几何
一、图像之间的基础矩阵
1.1、代码实现
1.2、结果截图
1.3、小结
二、极点和极线
1.1、代码实现
1.2、结果截图
1.3 、小结
三、图像集
四、遇到的问题
五、总结
一、图像之间的基础矩阵
1.1、代码实现
1 # -*- coding: utf-8 -*- 2 3 from PIL import Image 4 from numpy import * 5 from pylab import * 6 import numpy as np 7 8 from PCV.geometry import camera 9 from PCV.geometry import homography 10 from PCV.geometry import sfm 11 from PCV.localdescriptors import sift 12 13 14 camera = reload(camera) 15 homography = reload(homography) 16 sfm = reload(sfm) 17 sift = reload(sift) 18 19 # Read features 20 im1 = array(Image.open('jia/1.jpg')) 21 im2 = array(Image.open('jia/2.jpg')) 22 23 24 sift.process_image('jia/1.jpg', 'im1.sift') 25 l1, d1 =sift.read_features_from_file('im1.sift') 26 27 sift.process_image('jia/2.jpg', 'im2.sift') 28 l2, d2 =sift.read_features_from_file('im2.sift') 29 30 matches = sift.match_twosided(d1, d2) 31 32 ndx = matches.nonzero()[0] 33 x1 = homography.make_homog(l1[ndx, :2].T) 34 ndx2 = [int(matches[i]) for i in ndx] 35 x2 = homography.make_homog(l2[ndx2, :2].T) 36 37 d1n = d1[ndx] 38 d2n = d2[ndx2] 39 x1n = x1.copy() 40 x2n = x2.copy() 41 42 figure(figsize=(16,16)) 43 sift.plot_matches(im1, im2, l1, l2, matches, True) 44 show() 45 46 #def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6): 47 def F_from_ransac(x1, x2, model, maxiter=5000, match_threshold=1e-6): 48 """ Robust estimation of a fundamental matrix F from point 49 correspondences using RANSAC (ransac.py from 50 http://www.scipy.org/Cookbook/RANSAC). 51 52 input: x1, x2 (3*n arrays) points in hom. coordinates. """ 53 54 from PCV.tools import ransac 55 data = np.vstack((x1, x2)) 56 d = 10 # 20 is the original 57 # compute F and return with inlier index 58 F, ransac_data = ransac.ransac(data.T, model, 59 8, maxiter, match_threshold, d, return_all=True) 60 return F, ransac_data['inliers'] 61 62 # find F through RANSAC 63 model = sfm.RansacModel() 64 F, inliers = F_from_ransac(x1n, x2n, model, maxiter=5000, match_threshold=1e-1) 65 print("F:", F) 66 67 P1 = array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0]]) 68 P2 = sfm.compute_P_from_fundamental(F) 69 70 print("P2:", P2) 71 72 # triangulate inliers and remove points not in front of both cameras 73 X = sfm.triangulate(x1n[:, inliers], x2n[:, inliers], P1, P2) 74 75 # plot the projection of X 76 cam1 = camera.Camera(P1) 77 cam2 = camera.Camera(P2) 78 x1p = cam1.project(X) 79 x2p = cam2.project(X) 80 81 figure(figsize=(16, 16)) 82 imj = sift.appendimages(im1, im2) 83 imj = vstack((imj, imj)) 84 85 imshow(imj) 86 87 cols1 = im1.shape[1] 88 rows1 = im1.shape[0] 89 for i in range(len(x1p[0])): 90 if (0<= x1p[0][i]<cols1) and (0<= x2p[0][i]<cols1) and (0<=x1p[1][i]<rows1) and (0<=x2p[1][i]<rows1): 91 plot([x1p[0][i], x2p[0][i]+cols1],[x1p[1][i], x2p[1][i]],'c') 92 axis('off') 93 show() 94 95 d1p = d1n[inliers] 96 d2p = d2n[inliers] 97 98 # Read features 99 im3 = array(Image.open('jia/3.jpg')) 100 sift.process_image('jia/3.jpg', 'im3.sift') 101 l3, d3 = sift.read_features_from_file('im3.sift') 102 103 matches13 = sift.match_twosided(d1p, d3) 104 105 ndx_13 = matches13.nonzero()[0] 106 x1_13 = homography.make_homog(x1p[:, ndx_13]) 107 ndx2_13 = [int(matches13[i]) for i in ndx_13] 108 x3_13 = homography.make_homog(l3[ndx2_13, :2].T) 109 110 figure(figsize=(16, 16)) 111 imj = sift.appendimages(im1, im3) 112 imj = vstack((imj, imj)) 113 114 imshow(imj) 115 116 cols1 = im1.shape[1] 117 rows1 = im1.shape[0] 118 for i in range(len(x1_13[0])): 119 if (0<= x1_13[0][i]<cols1) and (0<= x3_13[0][i]<cols1) and (0<=x1_13[1][i]<rows1) and (0<=x3_13[1][i]<rows1): 120 plot([x1_13[0][i], x3_13[0][i]+cols1],[x1_13[1][i], x3_13[1][i]],'c') 121 axis('off') 122 show() 123 124 P3 = sfm.compute_P(x3_13, X[:, ndx_13]) 125 126 print("P3:", P3) 127 128 print("P1:", P1) 129 print("P2:", P2) 130 print("P3:", P3)
调用的函数sfm.py:
1 from pylab import * 2 from numpy import * 3 from scipy import linalg 4 5 6 def compute_P(x,X): 7 """ Compute camera matrix from pairs of 8 2D-3D correspondences (in homog. coordinates). """ 9 10 n = x.shape[1] 11 if X.shape[1] != n: 12 raise ValueError("Number of points don't match.") 13 14 # create matrix for DLT solution 15 M = zeros((3*n,12+n)) 16 for i in range(n): 17 M[3*i,0:4] = X[:,i] 18 M[3*i+1,4:8] = X[:,i] 19 M[3*i+2,8:12] = X[:,i] 20 M[3*i:3*i+3,i+12] = -x[:,i] 21 22 U,S,V = linalg.svd(M) 23 24 return V[-1,:12].reshape((3,4)) 25 26 27 def triangulate_point(x1,x2,P1,P2): 28 """ Point pair triangulation from 29 least squares solution. """ 30 31 M = zeros((6,6)) 32 M[:3,:4] = P1 33 M[3:,:4] = P2 34 M[:3,4] = -x1 35 M[3:,5] = -x2 36 37 U,S,V = linalg.svd(M) 38 X = V[-1,:4] 39 40 return X / X[3] 41 42 43 def triangulate(x1,x2,P1,P2): 44 """ Two-view triangulation of points in 45 x1,x2 (3*n homog. coordinates). """ 46 47 n = x1.shape[1] 48 if x2.shape[1] != n: 49 raise ValueError("Number of points don't match.") 50 51 X = [ triangulate_point(x1[:,i],x2[:,i],P1,P2) for i in range(n)] 52 return array(X).T 53 54 55 def compute_fundamental(x1,x2): 56 """ Computes the fundamental matrix from corresponding points 57 (x1,x2 3*n arrays) using the 8 point algorithm. 58 Each row in the A matrix below is constructed as 59 [x'*x, x'*y, x', y'*x, y'*y, y', x, y, 1] """ 60 61 n = x1.shape[1] 62 if x2.shape[1] != n: 63 raise ValueError("Number of points don't match.") 64 65 # build matrix for equations 66 A = zeros((n,9)) 67 for i in range(n): 68 A[i] = [x1[0,i]*x2[0,i], x1[0,i]*x2[1,i], x1[0,i]*x2[2,i], 69 x1[1,i]*x2[0,i], x1[1,i]*x2[1,i], x1[1,i]*x2[2,i], 70 x1[2,i]*x2[0,i], x1[2,i]*x2[1,i], x1[2,i]*x2[2,i] ] 71 72 # compute linear least square solution 73 U,S,V = linalg.svd(A) 74 F = V[-1].reshape(3,3) 75 76 # constrain F 77 # make rank 2 by zeroing out last singular value 78 U,S,V = linalg.svd(F) 79 S[2] = 0 80 F = dot(U,dot(diag(S),V)) 81 82 return F/F[2,2] 83 84 85 def compute_epipole(F): 86 """ Computes the (right) epipole from a 87 fundamental matrix F. 88 (Use with F.T for left epipole.) """ 89 90 # return null space of F (Fx=0) 91 U,S,V = linalg.svd(F) 92 e = V[-1] 93 return e/e[2] 94 95 96 def plot_epipolar_line(im,F,x,epipole=None,show_epipole=True): 97 """ Plot the epipole and epipolar line F*x=0 98 in an image. F is the fundamental matrix 99 and x a point in the other image.""" 100 101 m,n = im.shape[:2] 102 line = dot(F,x) 103 104 # epipolar line parameter and values 105 t = linspace(0,n,100) 106 lt = array([(line[2]+line[0]*tt)/(-line[1]) for tt in t]) 107 108 # take only line points inside the image 109 ndx = (lt>=0) & (lt<m) 110 plot(t[ndx],lt[ndx],linewidth=2) 111 112 if show_epipole: 113 if epipole is None: 114 epipole = compute_epipole(F) 115 plot(epipole[0]/epipole[2],epipole[1]/epipole[2],'r*') 116 117 118 def skew(a): 119 """ Skew matrix A such that a x v = Av for any v. """ 120 121 return array([[0,-a[2],a[1]],[a[2],0,-a[0]],[-a[1],a[0],0]]) 122 123 124 def compute_P_from_fundamental(F): 125 """ Computes the second camera matrix (assuming P1 = [I 0]) 126 from a fundamental matrix. """ 127 128 e = compute_epipole(F.T) # left epipole 129 Te = skew(e) 130 return vstack((dot(Te,F.T).T,e)).T 131 132 133 def compute_P_from_essential(E): 134 """ Computes the second camera matrix (assuming P1 = [I 0]) 135 from an essential matrix. Output is a list of four 136 possible camera matrices. """ 137 138 # make sure E is rank 2 139 U,S,V = svd(E) 140 if det(dot(U,V))<0: 141 V = -V 142 E = dot(U,dot(diag([1,1,0]),V)) 143 144 # create matrices (Hartley p 258) 145 Z = skew([0,0,-1]) 146 W = array([[0,-1,0],[1,0,0],[0,0,1]]) 147 148 # return all four solutions 149 P2 = [vstack((dot(U,dot(W,V)).T,U[:,2])).T, 150 vstack((dot(U,dot(W,V)).T,-U[:,2])).T, 151 vstack((dot(U,dot(W.T,V)).T,U[:,2])).T, 152 vstack((dot(U,dot(W.T,V)).T,-U[:,2])).T] 153 154 return P2 155 156 157 def compute_fundamental_normalized(x1,x2): 158 """ Computes the fundamental matrix from corresponding points 159 (x1,x2 3*n arrays) using the normalized 8 point algorithm. """ 160 161 n = x1.shape[1] 162 if x2.shape[1] != n: 163 raise ValueError("Number of points don't match.") 164 165 # normalize image coordinates 166 x1 = x1 / x1[2] 167 mean_1 = mean(x1[:2],axis=1) 168 S1 = sqrt(2) / std(x1[:2]) 169 T1 = array([[S1,0,-S1*mean_1[0]],[0,S1,-S1*mean_1[1]],[0,0,1]]) 170 x1 = dot(T1,x1) 171 172 x2 = x2 / x2[2] 173 mean_2 = mean(x2[:2],axis=1) 174 S2 = sqrt(2) / std(x2[:2]) 175 T2 = array([[S2,0,-S2*mean_2[0]],[0,S2,-S2*mean_2[1]],[0,0,1]]) 176 x2 = dot(T2,x2) 177 178 # compute F with the normalized coordinates 179 F = compute_fundamental(x1,x2) 180 181 # reverse normalization 182 F = dot(T1.T,dot(F,T2)) 183 184 return F/F[2,2] 185 186 187 class RansacModel(object): 188 """ Class for fundmental matrix fit with ransac.py from 189 http://www.scipy.org/Cookbook/RANSAC""" 190 191 def __init__(self,debug=False): 192 self.debug = debug 193 194 def fit(self,data): 195 """ Estimate fundamental matrix using eight 196 selected correspondences. """ 197 198 # transpose and split data into the two point sets 199 data = data.T 200 x1 = data[:3,:8] 201 x2 = data[3:,:8] 202 203 # estimate fundamental matrix and return 204 F = compute_fundamental_normalized(x1,x2) 205 return F 206 207 def get_error(self,data,F): 208 """ Compute x^T F x for all correspondences, 209 return error for each transformed point. """ 210 211 # transpose and split data into the two point 212 data = data.T 213 x1 = data[:3] 214 x2 = data[3:] 215 216 # Sampson distance as error measure 217 Fx1 = dot(F,x1) 218 Fx2 = dot(F,x2) 219 denom = Fx1[0]**2 + Fx1[1]**2 + Fx2[0]**2 + Fx2[1]**2 220 err = ( diag(dot(x1.T,dot(F,x2))) )**2 / denom 221 222 # return error per point 223 return err 224 225 226 def F_from_ransac(x1,x2,model,maxiter=5000,match_theshold=1e-6): 227 """ Robust estimation of a fundamental matrix F from point 228 correspondences using RANSAC (ransac.py from 229 http://www.scipy.org/Cookbook/RANSAC). 230 231 input: x1,x2 (3*n arrays) points in hom. coordinates. """ 232 233 from PCV.tools import ransac 234 235 data = vstack((x1,x2)) 236 237 # compute F and return with inlier index 238 F,ransac_data = ransac.ransac(data.T,model,8,maxiter,match_theshold,20,return_all=True) 239 return F, ransac_data['inliers']
1.2、结果截图
水平拍摄:
sift特征匹配:

图一
基础矩阵和投影矩阵:

Ransac算法剔除坏的匹配点:

图二
8点算法匹配:

图三

左右拍摄:
sift特征匹配:

图四
基础矩阵和投影矩阵:
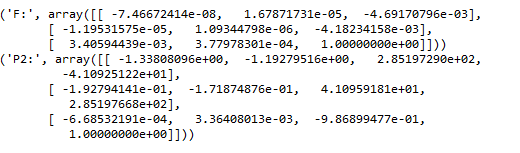
Ransac算法剔除坏的匹配点:

图五
8点算法匹配:

图六
基础矩阵:

前后拍摄:
sift特征匹配:

图七
基础矩阵和投影矩阵:
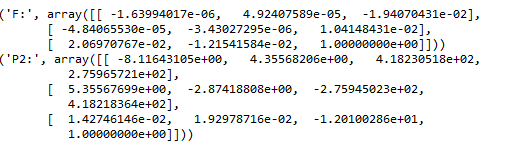
Ransac算法剔除坏的匹配点:

图八
8点算法匹配:

图九
两组图像的基础矩阵:
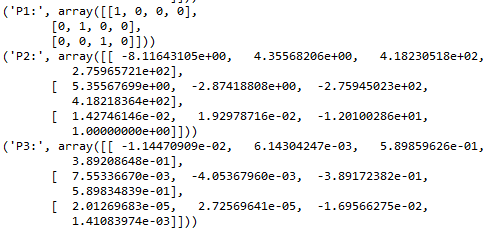
1.3、小结:提取sift特征后匹配sift特征,之后用ransac算法剔除错配的特征,然后用8点算法来求出空间中两张蹄片对应的点的坐标。
二、极点和极线
1.1、代码实现
1 # -*- coding: utf-8 -*- 2 import numpy as np 3 import cv2 as cv 4 from matplotlib import pyplot as plt 5 img1 = cv.imread('D:/new/beizi/1.jpg',0) #索引图像 # left image 6 img2 = cv.imread('D:/new/beizi/2.jpg',0) #训练图像 # right image 7 sift = cv.xfeatures2d.SIFT_create() 8 # 使用SIFT查找关键点和描述符 9 kp1, des1 = sift.detectAndCompute(img1,None) 10 kp2, des2 = sift.detectAndCompute(img2,None) 11 # FLANN 参数 12 FLANN_INDEX_KDTREE = 1 13 index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5) 14 search_params = dict(checks=50) 15 flann = cv.FlannBasedMatcher(index_params,search_params) 16 matches = flann.knnMatch(des1,des2,k=2) 17 good = [] 18 pts1 = [] 19 pts2 = [] 20 21 for i,(m,n) in enumerate(matches): 22 if m.distance < 0.8*n.distance: 23 good.append(m) 24 pts2.append(kp2[m.trainIdx].pt) 25 pts1.append(kp1[m.queryIdx].pt) 26 pts1 = np.int32(pts1) 27 pts2 = np.int32(pts2) 28 F, mask = cv.findFundamentalMat(pts1,pts2,cv.FM_LMEDS) 29 # 我们只选择内点 30 pts1 = pts1[mask.ravel()==1] 31 pts2 = pts2[mask.ravel()==1] 32 def drawlines(img1,img2,lines,pts1,pts2): 33 ''' img1 - 我们在img2相应位置绘制极点生成的图像 34 lines - 对应的极点 ''' 35 r,c = img1.shape 36 img1 = cv.cvtColor(img1,cv.COLOR_GRAY2BGR) 37 img2 = cv.cvtColor(img2,cv.COLOR_GRAY2BGR) 38 for r,pt1,pt2 in zip(lines,pts1,pts2): 39 color = tuple(np.random.randint(0,255,3).tolist()) 40 x0,y0 = map(int, [0, -r[2]/r[1] ]) 41 x1,y1 = map(int, [c, -(r[2]+r[0]*c)/r[1] ]) 42 img1 = cv.line(img1, (x0,y0), (x1,y1), color,1) 43 img1 = cv.circle(img1,tuple(pt1),5,color,-1) 44 img2 = cv.circle(img2,tuple(pt2),5,color,-1) 45 return img1,img2 46 # 在右图(第二张图)中找到与点相对应的极点,然后在左图绘制极线 47 lines1 = cv.computeCorrespondEpilines(pts2.reshape(-1,1,2), 2,F) 48 lines1 = lines1.reshape(-1,3) 49 img5,img6 = drawlines(img1,img2,lines1,pts1,pts2) 50 # 在左图(第一张图)中找到与点相对应的Epilines,然后在正确的图像上绘制极线 51 lines2 = cv.computeCorrespondEpilines(pts1.reshape(-1,1,2), 1,F) 52 lines2 = lines2.reshape(-1,3) 53 img3,img4 = drawlines(img2,img1,lines2,pts2,pts1) 54 plt.subplot(121),plt.imshow(img5) 55 plt.subplot(122),plt.imshow(img3) 56 plt.show()
1.2、结果截图
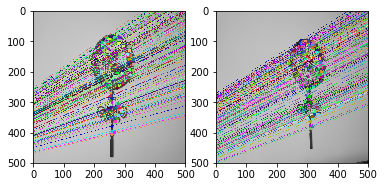
1.3 、小结:利用SIFT查找关键点和描述符,在图中找到极点,然后用plot绘画出外极线。
三、图像集
图像集didi:

图像集jia:

图像集beizi:

四、遇到的问题
4.1、图像的运行出现
did not meet fit acceptance criteria
持续报错,然后我就重新多拍了几组图片,换了好几组才成功的,可能是因为图像的拍摄不再一个水平和背景过于丰富。
4.2、画外极线是报错
'module' object has no attribute 'SIFT'
我找了朋友给我看了一下,跟着他改的代码就运行成功了。
五、总结
首先,图片的拍摄还是有一定的要求,我们拍摄的图片要背景不要过于丰富,尽量在一个水平线上,保持图像的清晰度,因为不清晰可能会报错或者影响实验结果,然后从三组不同的拍摄角度的图片来运行,可以看出sift匹配的点很多,室内的景使用Ransac算法剔除的坏点较多,室外的景使用的Ransac算法剔除的坏点较少,说明Ransac算法对外景的处理比较有效。从运行结果看出,外景使用8点算法匹配比较有效。求出来的基础矩阵都是三行三列,行列式值等于0(秩为2的3阶方阵),是有七个参数,其中两个参数是对级,三个参数表示两个像平面的单应性矩阵。