现在的大部分方法都通过调整网络结构,使网络具有获得更丰富表示特征的能力,如attention、AutoML、NAS。
本文提出的自校准卷积(Self-Calibrated conv),通过增强每一层卷积的能力,提升整个网络的能力。SC conv将原卷积分为多个不同的部分,由于这种异质的卷积操作和核之间的交流,每个位置的感受野都被扩大了。
优点:每一个空间位置都可以适应性地编码长距离区域中的信息【non-local】;是一个通用的方法可以很容易地应用到标准卷积层中,而不需要引入其他参数。
个人认为他是一个non-local+multi-scale的操作,同时又没有引入其他参数。
传统卷积层F
与一组卷积核$K=[k_1, k_2, ..., k_{widehat{C}}]$.
那么第i个通道的输出可以表示为$y_i=k_i*X=sum_{j=1}^Ck_i^j*x_j$, 所以每一个特征图都是将所有通道的输出相加,而每个通道都是重复该式。这样卷积核学习到的特征是非常相近的。卷积特征变换中每个空间位置的感受野也主要由预定义的卷积核尺寸决定,由这样的卷积层堆叠成的网络由于缺乏大感受野而难以捕捉高层语义信息。
自校准卷积
将输入划分为了两个分支,一半进行自校准操作得到$Y_1$,另一半进行正常卷积操作得到$Y_2=F_1(X_2)=X_2*K_1$。最终将$Y_1$和$Y_2$拼接得到$Y$。
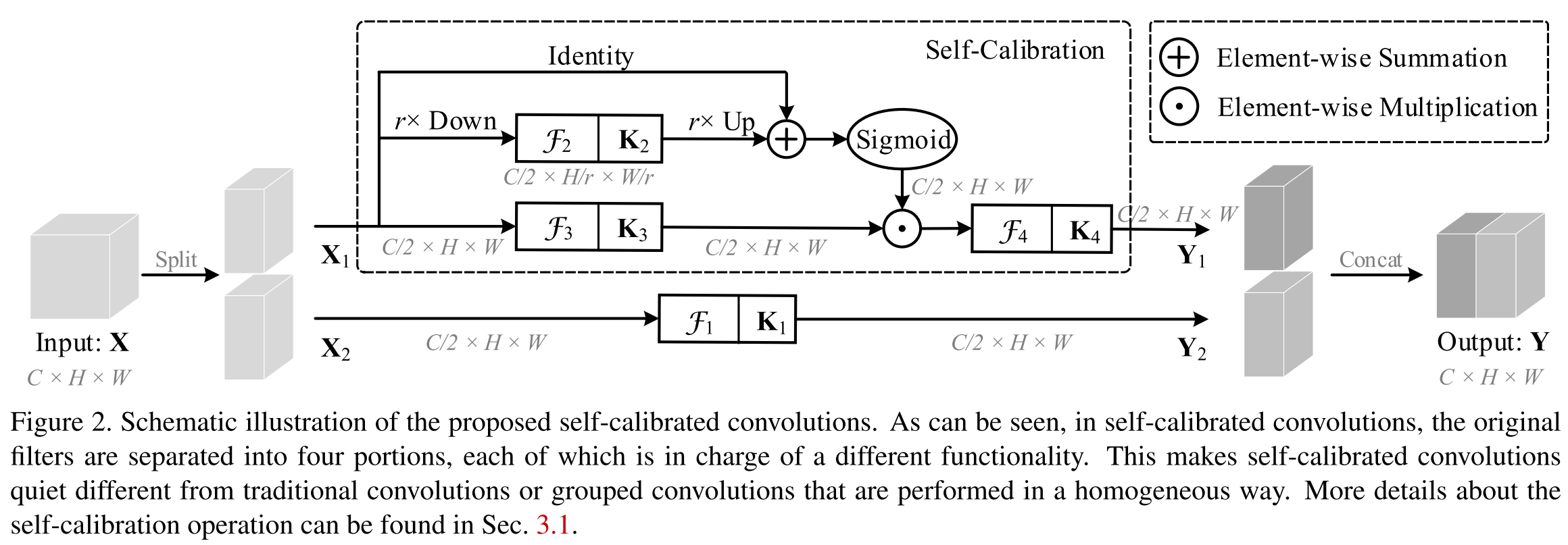
自校准操作在两个尺度空间进行卷积变换,一个尺度空间与输入特征图的分辨率相同,另一个尺度空间则进行过下采样。
对于给定的$X_1$, $T_1=AvgPool_r(X_1)$
$X_1'=Up(F_2(T_1))=Up(T_1*K_2), Up(cdot)$为双线性插值。
$Y_1'=F_3(X_1)cdotsigma(X_1+X_1'), F_3(X_1)=X_1*K_3, sigma$为sigmoid函数
$Y_1=F_4(Y_1')=Y_1'*K_4$
与Group Conv相比,GroupConv是同质地在多个并行分支中或结构化地方式中进行卷积。而SC conv则是一种异构的方式,因此每个位置都可以融合两个空间尺度空间的信息。
与额外加入的注意力模块相比,SC conv是改变了卷积的内部操作,并不需要引入额外参数。
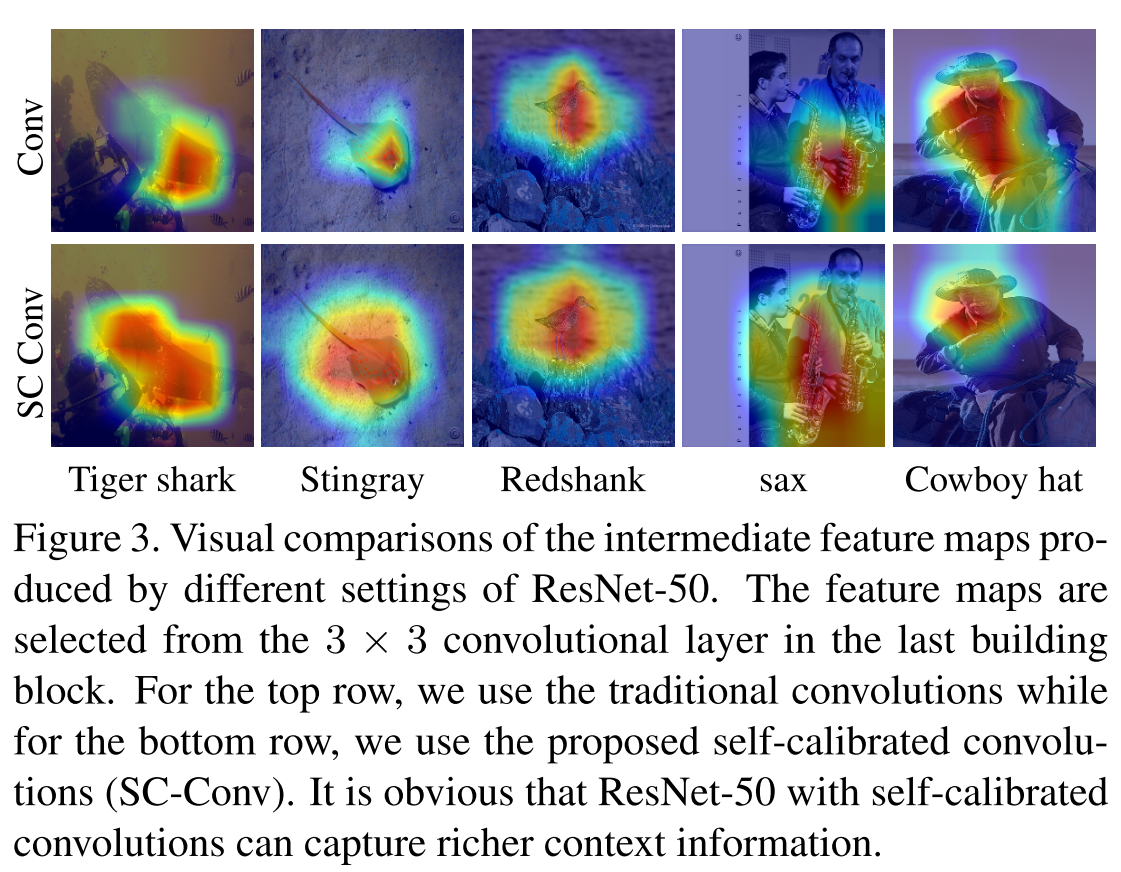
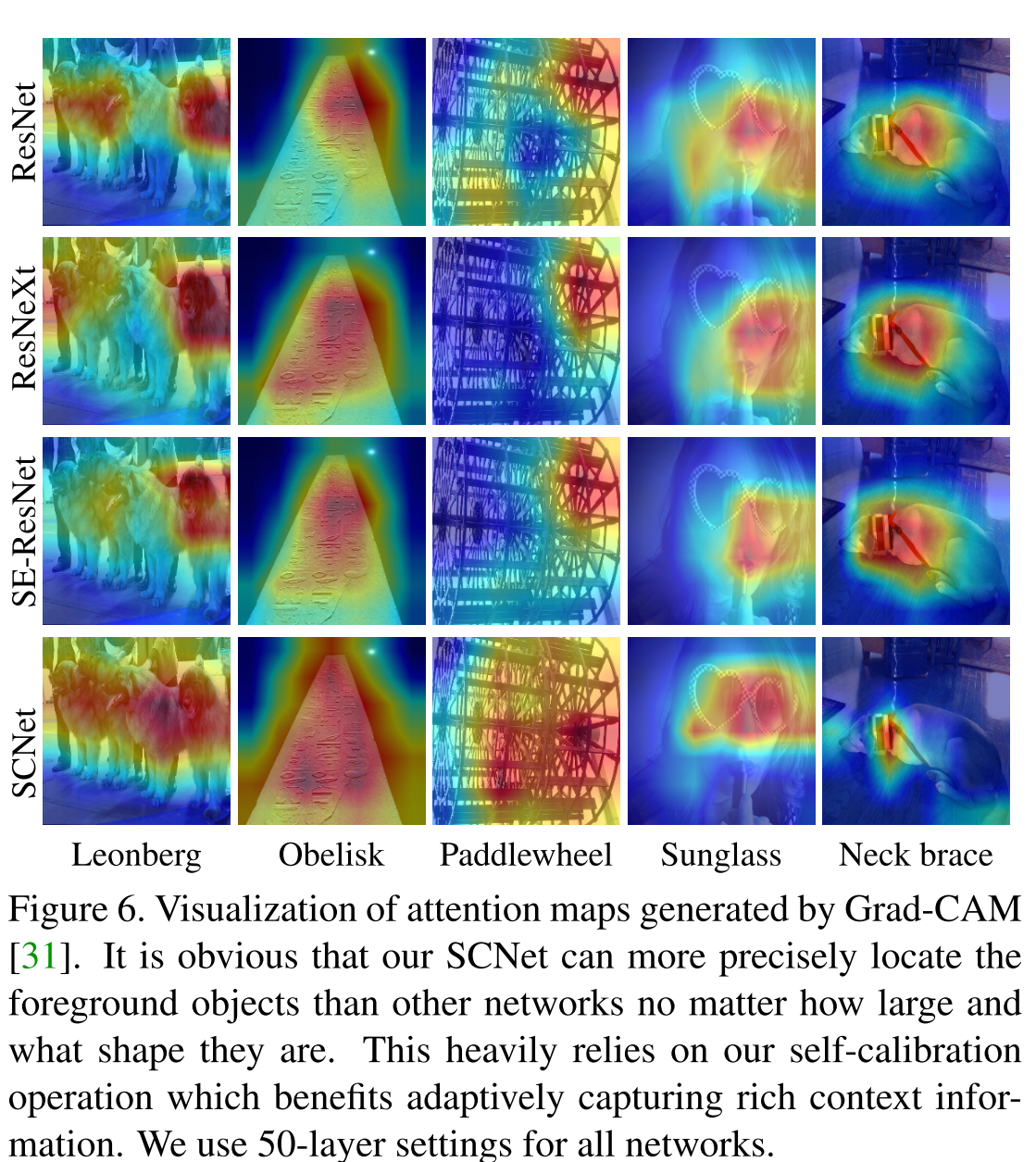
可以看出,与注意力相比,SC conv可以更准确定位目标物体而不会包括过多的背景部分。这说明自校准卷积对于识别小的整体目标是更有效的。