题目:输入一个整数数组,判断该数组是不是某二叉树的后序遍历的结果.如果是则返回true,否则返回false.假设输入的数组的任意两个数字互不相同.
例如输入数组{5,7,6,9,11,10,8},则返回true,因为这个整数序列是下图二叉树的后序遍历的结果.如果输入的数组是{7,4,6,5},由于没有哪棵二叉搜索树的后序遍历的结果是这个序列,因此返回false.
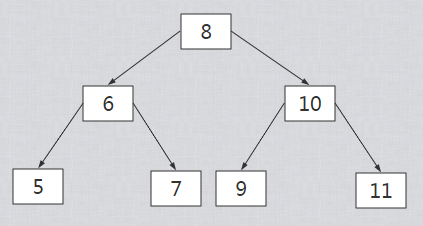
后序遍历序列5、7、6、9、11、10、8对应的二叉搜索树
在后序遍历得到的序列中,最后一个数字是根结点的值.数组中前面的数字可以分为两部分:第一部分是左子树结点的值,他们都比根结点的值小;第二部分是右节点的值,他们都比根结点的值大.
以数组{5,7,6,9,11,10,8}为例,后序遍历的结果的最后一个数字8就是根结点的值.在这个数组中,前3个数字5,7和6都比8小,是值为8的结点的左子树结点;后3个数字9,11,10都比8大,是值为8的结点的右子树结点.
我们接下来用同样的方法确定与数组每一部分对应子树的结构.这其实就是一个递归的过程.对于序列5,7,6,最后一个数字6是左结点的根结点的值.数字5比6小,是值为6结点的左子结点,而7是它的右子节点.同样,在序列9,11,10中,最后一个数字10是右子树的根结点,数字9比10小,是值为10的结点的左子结点,而11则是它的右子节点.
我们再来分析另一个整数数组{7,4,6,5}.后序遍历的最后一个数是根结点,因此在对应的二叉搜索树中,根结点上是没有左子树的,数字7,4,6都是右子树结点的值.但我们发现在右子树有一个结点的值是4,比根结点的值5小,这就违背了二叉搜索树的定义.因此不存在一棵二叉树,它的后序遍历的结果是7,4,6,5.
找到规律后再写代码,就不是一件很困难的事情了.下面是参考代码:
1 bool VerifySquenceOfBST(int sequence[],int length) 2 3 { 4 5 if(sequence==NULL||length<=0) 6 7 return false; 8 9 int root=sequence[length-1]; 10 11 12 13 //在二叉搜索树中左子树的结点小于根结点 14 15 int i=0; 16 17 for(;i<length-1;++i) 18 19 { 20 21 if(sequence[i]>root) 22 23 break; 24 25 } 26 27 28 29 //在二叉搜索树中右子树的结点大于根结点 30 31 int j=i; 32 33 for(;j<length-1;++j) 34 35 { 36 37 if(sequence[j]<root) 38 39 return false; 40 41 } 42 43 44 45 //判断左子树是不是二叉搜索树 46 47 bool left=true; 48 49 if(i>0) 50 51 left=VerifySquenceOfBST(sequence,i); 52 53 54 55 //判断右子树是不是二叉搜索树 56 57 bool right=true; 58 59 if(i<length-1) 60 61 right=VerifySequenceOfBST(sequence+i,length-i-1); 62 63 64 65 return (left&&right); 66 67 }