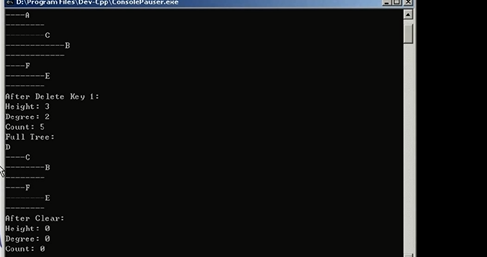
1.#include <stdio.h>
#include <stdlib.h>
#include "BSTree.h"
/* 二叉树排序算法 */
struct Node
{
BSTreeNode header;
char v;
};
void printf_data(BSTreeNode* node)
{
if( node != NULL )
{
printf("%c", ((struct Node*)node)->v);
}
}
int compare_key(BSKey* k1, BSKey* k2)
{
return (int)k1 - (int)k2;
}
int main(int argc, char *argv[])
{
BSTree* tree = BSTree_Create();
struct Node n1 = {{(BSKey*)1, NULL, NULL}, 'A'};
struct Node n2 = {{(BSKey*)2, NULL, NULL}, 'B'};
struct Node n3 = {{(BSKey*)3, NULL, NULL}, 'C'};
struct Node n4 = {{(BSKey*)4, NULL, NULL}, 'D'};
struct Node n5 = {{(BSKey*)5, NULL, NULL}, 'E'};
struct Node n6 = {{(BSKey*)6, NULL, NULL}, 'F'};
BSTree_Insert(tree, (BSTreeNode*)&n4, compare_key);
BSTree_Insert(tree, (BSTreeNode*)&n1, compare_key);
BSTree_Insert(tree, (BSTreeNode*)&n3, compare_key);
BSTree_Insert(tree, (BSTreeNode*)&n6, compare_key);
BSTree_Insert(tree, (BSTreeNode*)&n2, compare_key);
BSTree_Insert(tree, (BSTreeNode*)&n5, compare_key);
printf("Height: %d
", BSTree_Height(tree));
printf("Degree: %d
", BSTree_Degree(tree));
printf("Count: %d
", BSTree_Count(tree));
printf("Search Key 5: %c
", ((struct Node*)BSTree_Get(tree, (BSKey*)5, compare_key))->v);
printf("Full Tree:
");
BSTree_Display(tree, printf_data, 4, '-');
BSTree_Delete(tree, (BSKey*)4, compare_key);
printf("After Delete Key 4:
");
printf("Height: %d
", BSTree_Height(tree));
printf("Degree: %d
", BSTree_Degree(tree));
printf("Count: %d
", BSTree_Count(tree));
printf("Full Tree:
");
BSTree_Display(tree, printf_data, 4, '-');
BSTree_Clear(tree);
printf("After Clear:
");
printf("Height: %d
", BSTree_Height(tree));
printf("Degree: %d
", BSTree_Degree(tree));
printf("Count: %d
", BSTree_Count(tree));
BSTree_Display(tree, printf_data, 4, '-');
BSTree_Destroy(tree);
return 0;
}
2.#ifndef _BSTREE_H_
#define _BSTREE_H_
typedef void BSTree;
typedef void BSKey; //关键字的类型
typedef struct _tag_BSTreeNode BSTreeNode;
/* 二叉排序来源于二分查找 */
struct _tag_BSTreeNode
{
BSKey* key; //关键字
BSTreeNode* left;
BSTreeNode* right;
};
typedef void (BSTree_Printf)(BSTreeNode*);
//定义一个比较函数
typedef int (BSTree_Compare)(BSKey*, BSKey*);
BSTree* BSTree_Create();
void BSTree_Destroy(BSTree* tree);
void BSTree_Clear(BSTree* tree);
//compare-->通过比较插入;BSTree_Compare函数比较指针;
int BSTree_Insert(BSTree* tree, BSTreeNode* node, BSTree_Compare* compare);
BSTreeNode* BSTree_Delete(BSTree* tree, BSKey* key, BSTree_Compare* compare);
BSTreeNode* BSTree_Get(BSTree* tree, BSKey* key, BSTree_Compare* compare);
BSTreeNode* BSTree_Root(BSTree* tree);
int BSTree_Height(BSTree* tree);
int BSTree_Count(BSTree* tree);
int BSTree_Degree(BSTree* tree);
void BSTree_Display(BSTree* tree, BSTree_Printf* pFunc, int gap, char div);
#endif
3.#include <stdio.h>
#include <malloc.h>
#include "BSTree.h"
typedef struct _tag_BSTree TBSTree;
struct _tag_BSTree
{
int count;
BSTreeNode* root;
};
//递归显示
static void recursive_display(BSTreeNode* node, BSTree_Printf* pFunc, int format, int gap, char div) // O(n)
{
int i = 0;
if( (node != NULL) && (pFunc != NULL) )
{
for(i=0; i<format; i++)
{
printf("%c", div);
}
pFunc(node);
printf("
");
if( (node->left != NULL) || (node->right != NULL) )
{
recursive_display(node->left, pFunc, format + gap, gap, div);
recursive_display(node->right, pFunc, format + gap, gap, div);
}
}
else
{
for(i=0; i<format; i++)
{
printf("%c", div);
}
printf("
");
}
}
//节点数
static int recursive_count(BSTreeNode* root) // O(n)
{
int ret = 0;
if( root != NULL )
{
ret = recursive_count(root->left) + 1 + recursive_count(root->right);
}
return ret;
}
//高度
static int recursive_height(BSTreeNode* root) // O(n)
{
int ret = 0;
if( root != NULL )
{
int lh = recursive_height(root->left);
int rh = recursive_height(root->right);
ret = ((lh > rh) ? lh : rh) + 1;
}
return ret;
}
//递归度
static int recursive_degree(BSTreeNode* root) // O(n)
{
int ret = 0;
if( root != NULL )
{
if( root->left != NULL )
{
ret++;
}
if( root->right != NULL )
{
ret++;
}
if( ret == 1 )
{
int ld = recursive_degree(root->left);
int rd = recursive_degree(root->right);
if( ret < ld )
{
ret = ld;
}
if( ret < rd )
{
ret = rd;
}
}
}
return ret;
}
//insert
static int recursive_insert(BSTreeNode* root, BSTreeNode* node, BSTree_Compare* compare)
{
int ret = 1;
//先进行比较
int r = compare(node->key, root->key);
if( r == 0 )
{
ret = 0;
}
//左节点
else if( r < 0 )
{
if( root->left != NULL )
{
ret = recursive_insert(root->left, node, compare);
}
else
{
root->left = node;
}
}
//右节点
else if( r > 0 )
{
if( root->right != NULL )
{
ret = recursive_insert(root->right, node, compare);
}
else
{
root->right = node;
}
}
}
//递归查询
static BSTreeNode* recursive_get(BSTreeNode* root, BSKey* key, BSTree_Compare* compare)
{
BSTreeNode* ret = NULL;
if( root != NULL )
{
int r = compare(key, root->key);
if( r == 0 )
{
ret = root;
}
//左查找
else if( r < 0 )
{
ret = recursive_get(root->left, key, compare);
}
//右查找
else if( r > 0 )
{
ret = recursive_get(root->right, key, compare);
}
}
return ret;
}
//delete 节点
static BSTreeNode* delete_node(BSTreeNode** pRoot)
{
BSTreeNode* ret = *pRoot;
//判断是否在左右子树 三种情况 -->仅左右孩子 有两个孩子
if( (*pRoot)->right == NULL )
{
*pRoot = (*pRoot)->left;
}
else if( (*pRoot)->left == NULL )
{
*pRoot = (*pRoot)->right;
}
else
{
//子树的子树
BSTreeNode* g = *pRoot;
BSTreeNode* c = (*pRoot)->left;
while( c->right != NULL )
{
g = c;
c = c->right;
}
if( g != *pRoot )
{
g->right = c->left;
}
else
{
g->left = c->left;
}
//
c->left = (*pRoot)->left;
c->right = (*pRoot)->right;
*pRoot = c;
}
return ret;
}
//删除 之后还是一颗二叉树 pRoot指向指针指针
static BSTreeNode* recursive_delete(BSTreeNode** pRoot, BSKey* key, BSTree_Compare* compare)
{
BSTreeNode* ret = NULL;
//*pRoot根节点
if( (pRoot != NULL) && (*pRoot != NULL) )
{
//首先根据根节点进行比较
int r = compare(key, (*pRoot)->key);
//删除根节点
if( r == 0 )
{
ret = delete_node(pRoot);
}
//不然有左边子树
else if( r < 0 )
{
ret = recursive_delete(&((*pRoot)->left), key, compare);
}
//否则
else if( r > 0 )
{
ret = recursive_delete(&((*pRoot)->right), key, compare);
}
}
return ret;
}
//创建一颗二叉树
BSTree* BSTree_Create() // O(1)
{
TBSTree* ret = (TBSTree*)malloc(sizeof(TBSTree));
if( ret != NULL )
{
ret->count = 0;
ret->root = NULL;
}
return ret;
}
//销毁二叉树
void BSTree_Destroy(BSTree* tree) // O(1)
{
free(tree);
}
//清除二叉树
void BSTree_Clear(BSTree* tree) // O(1)
{
TBSTree* btree = (TBSTree*)tree;
if( btree != NULL )
{
btree->count = 0;
btree->root = NULL;
}
}
//根据节点插入
int BSTree_Insert(BSTree* tree, BSTreeNode* node, BSTree_Compare* compare)
{
TBSTree* btree = (TBSTree*)tree;
int ret = (btree != NULL) && (node != NULL) && (compare != NULL);
if( ret )
{
node->left = NULL;
node->right = NULL;
if( btree->root == NULL )
{
btree->root = node;
}
else
{
ret = recursive_insert(btree->root, node, compare);
}
if( ret )
{
btree->count++;
}
}
return ret;
}
//通过关键字删除元素
BSTreeNode* BSTree_Delete(BSTree* tree, BSKey* key, BSTree_Compare* compare)
{
TBSTree* btree = (TBSTree*)tree;
BSTreeNode* ret = NULL;
if( (btree != NULL) && (key != NULL) && (compare != NULL) )
{
ret = recursive_delete(&btree->root, key, compare);
if( ret != NULL )
{
btree->count--;
}
}
return ret;
}
BSTreeNode* BSTree_Get(BSTree* tree, BSKey* key, BSTree_Compare* compare)
{
TBSTree* btree = (TBSTree*)tree;
BSTreeNode* ret = NULL;
if( (btree != NULL) && (key != NULL) && (compare != NULL) )
{
ret = recursive_get(btree->root, key, compare);
}
return ret;
}
BSTreeNode* BSTree_Root(BSTree* tree) // O(1)
{
TBSTree* btree = (TBSTree*)tree;
BSTreeNode* ret = NULL;
if( btree != NULL )
{
ret = btree->root;
}
return ret;
}
int BSTree_Height(BSTree* tree) // O(n)
{
TBSTree* btree = (TBSTree*)tree;
int ret = 0;
if( btree != NULL )
{
ret = recursive_height(btree->root);
}
return ret;
}
int BSTree_Count(BSTree* tree) // O(1)
{
TBSTree* btree = (TBSTree*)tree;
int ret = 0;
if( btree != NULL )
{
ret = btree->count;
}
return ret;
}
int BSTree_Degree(BSTree* tree) // O(n)
{
TBSTree* btree = (TBSTree*)tree;
int ret = 0;
if( btree != NULL )
{
ret = recursive_degree(btree->root);
}
return ret;
}
void BSTree_Display(BSTree* tree, BSTree_Printf* pFunc, int gap, char div) // O(n)
{
TBSTree* btree = (TBSTree*)tree;
if( btree != NULL )
{
recursive_display(btree->root, pFunc, 0, gap, div);
}
}