动态规划____装配线 两行并行,区分状态转移方向

1.long long 使用 %lld读&写

2.两行并行的DP(两行之中每一个状态的状态转移方向不同[虽然类似]),所以要写两个转移函数

3.需要注意的代码:

int f1(int index)
{
    if(dp1[index] != INF)
        return dp1[index] ;
    if(index == 1)//不要想当然的把结尾当作0
        return dp1[index] = time1[0] + time1[1];//结尾处不仅要加time1[0],也要加time1[1]
    else return dp1[index] = min( f1(index-1) , time2to1[index-2] + f2(index-1) ) + time1[index];
                               //绿色的数字仔细分析一下就有了
}

4.下列代码无需研究,跟上面基本相同,只是为了回顾时候熟悉此题的解题方法

int f2(int index)
{
    if(dp2[index] != INF)
        return dp2[index];
    if(index == 1)
        return dp2[index] = time2[0] + time2[1];
    else return dp2[index] = min( f2(index-1) , time1to2[index-2] + f1(index-1)) +  time2[index]; 
}

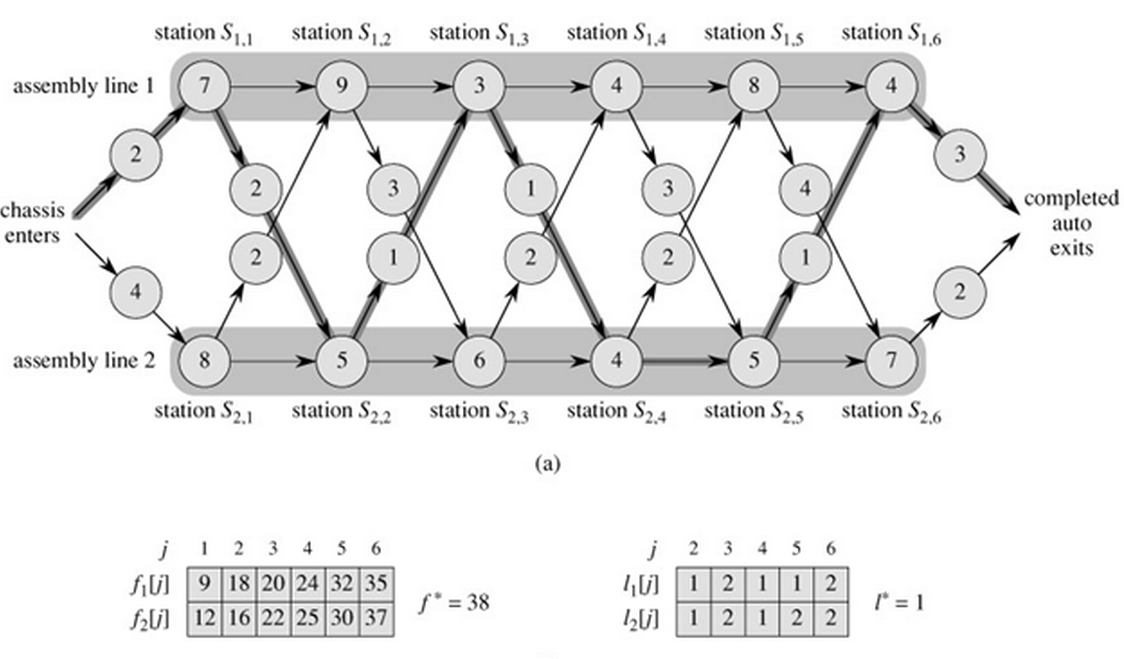
5.以下内容为 简要思路 与 题目样图,一眼带过即可

 

递归定义最优解的值

合并后可以达到下面两个递归式：

  

 

例子(图与输入样例):

6
2 7 9 3 4 8 4 3
4 8 5 6 4 5 7 2
2 3 1 3 4
2 1 2 2 1 

此题在hrbustOJ需要开long long,AC代码折叠在下方

#include <cstdio>
#include <cstring>
#include <iostream>
#define MAX 1000010
#define INF -1

using namespace std;
long long f1(long long index);
long long f2(long long index);
long long min(long long a, long long b);

long long n;
long long time1[MAX];
long long time2[MAX];
long long time1to2[MAX];
long long time2to1[MAX];
long long dp1[MAX], dp2[MAX];

long long min(long long a, long long b)
{
    return a<b?a:b;
}

long long f1(long long index)
{
    if(dp1[index] != INF)
        return dp1[index] ;
    if(index == 1)
        return dp1[index] = time1[0] + time1[1];
    else return dp1[index] = min( f1(index-1) , time2to1[index-2] + f2(index-1) ) + time1[index]; 
}

long long f2(long long index)
{
    if(dp2[index] != INF)
        return dp2[index];
    if(index == 1)
        return dp2[index] = time2[0] + time2[1];
    else return dp2[index] = min( f2(index-1) , time1to2[index-2] + f1(index-1)) +  time2[index]; 
}

int main()
{
    long long i;

    //freopen("1.txt", "r", stdin);
    while( scanf("%d", &n) != EOF)
    {
        
        for( i = 0 ; i < n + 2; i++)
        {
            scanf("%lld", &time1[i]);
        }
        for( i = 0 ; i < n + 2; i++)
        {
            scanf("%lld", &time2[i]);
        }
        for( i = 0 ; i < n - 1; i++)
        {
            scanf("%lld", &time1to2[i]);
        }
        for( i = 0 ; i < n - 1; i++)
        {
            scanf("%lld", &time2to1[i]);
        }
        
        memset(dp1, INF, sizeof(dp1));
        memset(dp2, INF, sizeof(dp2));
        long long result = min(f1(n) + time1[n+1] , f2(n) + time2[n+1]);
        printf("%lld
", result);
    }
    return 0;
}