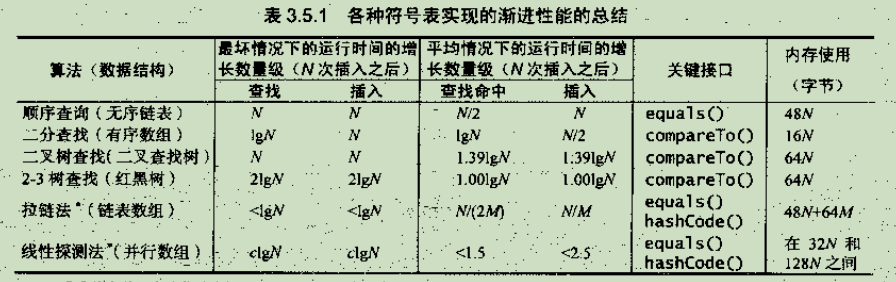
一、顺序查找(基于无序链表,效率低下)
package search; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class SequentialSearchST<Key, Value> { private int n; // number of key-value pairs private Node first; // the linked list of key-value pairs private class Node { private Key key; private Value val; private Node next; public Node(Key key, Value val, Node next) { this.key = key; this.val = val; this.next = next; } } public SequentialSearchST() { } public int size() { return n; } public boolean isEmpty() { return size() == 0; } //判断是否包含key public boolean contains(Key key) { if (key == null) throw new IllegalArgumentException("argument to contains() is null"); return get(key) != null; } //查找key的值 public Value get(Key key) { if (key == null) throw new IllegalArgumentException("argument to get() is null"); for (Node x = first; x != null; x = x.next) { if (key.equals(x.key)) return x.val; } return null; } //增加键值对 public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("first argument to put() is null"); if (val == null) { delete(key); return; } for (Node x = first; x != null; x = x.next) { if (key.equals(x.key)) { x.val = val; return; } } first = new Node(key, val, first); n++; } //删除 public void delete(Key key) { if (key == null) throw new IllegalArgumentException("argument to delete() is null"); first = delete(first, key); } // delete key in linked list beginning at Node x // warning: function call stack too large if table is large private Node delete(Node x, Key key) { if (x == null) return null; if (key.equals(x.key)) { n--; return x.next; } x.next = delete(x.next, key); return x; } public Iterable<Key> keys() { Queue<Key> queue = new Queue<Key>(); for (Node x = first; x != null; x = x.next) queue.enqueue(x.key); return queue; } public static void main(String[] args) { SequentialSearchST<String, Integer> st = new SequentialSearchST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); } }
二.有序数组中的二分查找
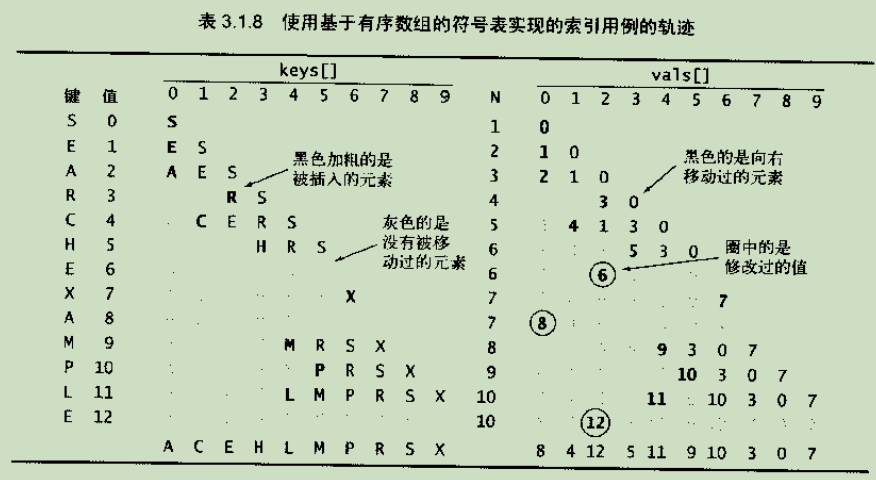
package search; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import java.util.NoSuchElementException; public class BinarySearchST<Key extends Comparable<Key>, Value> { private static final int INIT_CAPACITY = 2; private Key[] keys; private Value[] vals; private int n = 0; public BinarySearchST() { this(INIT_CAPACITY); } public BinarySearchST(int capacity) { keys = (Key[]) new Comparable[capacity]; vals = (Value[]) new Object[capacity]; } //数组扩容 private void resize(int capacity) { assert capacity >= n; Key[] tempk = (Key[]) new Comparable[capacity]; Value[] tempv = (Value[]) new Object[capacity]; for (int i = 0; i < n; i++) { tempk[i] = keys[i]; tempv[i] = vals[i]; } vals = tempv; keys = tempk; } public int size() { return n; } public boolean isEmpty() { return size() == 0; } //判断是否包含key public boolean contains(Key key) { if (key == null) throw new IllegalArgumentException("argument to contains() is null"); return get(key) != null; } //查找key的值 public Value get(Key key) { if (key == null) throw new IllegalArgumentException("argument to get() is null"); if (isEmpty()) return null; int i = rank(key); if (i < n && keys[i].compareTo(key) == 0) return vals[i]; return null; } //返回表中小于给定键的键的数量(二分查找) public int rank(Key key) { if (key == null) throw new IllegalArgumentException("argument to rank() is null"); int lo = 0, hi = n-1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; int cmp = key.compareTo(keys[mid]); if (cmp < 0) hi = mid - 1; else if (cmp > 0) lo = mid + 1; else return mid; } return lo; } //插入键值 public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("first argument to put() is null"); if (val == null) { delete(key); return; } int i = rank(key); // key已经存在于表中 if (i < n && keys[i].compareTo(key) == 0) { vals[i] = val; return; } // insert new key-value pair if (n == keys.length) resize(2*keys.length); for (int j = n; j > i; j--) { keys[j] = keys[j-1]; vals[j] = vals[j-1]; } keys[i] = key; vals[i] = val; n++; assert check(); } public void delete(Key key) { if (key == null) throw new IllegalArgumentException("argument to delete() is null"); if (isEmpty()) return; // compute rank int i = rank(key); // key not in table if (i == n || keys[i].compareTo(key) != 0) { return; } for (int j = i; j < n-1; j++) { keys[j] = keys[j+1]; vals[j] = vals[j+1]; } n--; keys[n] = null; // to avoid loitering vals[n] = null; // resize if 1/4 full if (n > 0 && n == keys.length/4) resize(keys.length/2); assert check(); } //删除最小键值对 public void deleteMin() { if (isEmpty()) throw new NoSuchElementException("Symbol table underflow error"); delete(min()); } //删除最大键值对 public void deleteMax() { if (isEmpty()) throw new NoSuchElementException("Symbol table underflow error"); delete(max()); } //最小值得键 public Key min() { if (isEmpty()) throw new NoSuchElementException("called min() with empty symbol table"); return keys[0]; } //最大值得键 public Key max() { if (isEmpty()) throw new NoSuchElementException("called max() with empty symbol table"); return keys[n-1]; } //查看索引k对应的key public Key select(int k) { if (k < 0 || k >= size()) { throw new IllegalArgumentException("called select() with invalid argument: " + k); } return keys[k]; } //向下取整 public Key floor(Key key) { if (key == null) throw new IllegalArgumentException("argument to floor() is null"); int i = rank(key); if (i < n && key.compareTo(keys[i]) == 0) return keys[i]; if (i == 0) return null; else return keys[i-1]; } //向下取整 public Key ceiling(Key key) { if (key == null) throw new IllegalArgumentException("argument to ceiling() is null"); int i = rank(key); if (i == n) return null; else return keys[i]; } public int size(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to size() is null"); if (hi == null) throw new IllegalArgumentException("second argument to size() is null"); if (lo.compareTo(hi) > 0) return 0; if (contains(hi)) return rank(hi) - rank(lo) + 1; else return rank(hi) - rank(lo); } public Iterable<Key> keys() { return keys(min(), max()); } public Iterable<Key> keys(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to keys() is null"); if (hi == null) throw new IllegalArgumentException("second argument to keys() is null"); Queue<Key> queue = new Queue<Key>(); if (lo.compareTo(hi) > 0) return queue; for (int i = rank(lo); i < rank(hi); i++) queue.enqueue(keys[i]); if (contains(hi)) queue.enqueue(keys[rank(hi)]); return queue; } private boolean check() { return isSorted() && rankCheck(); } private boolean isSorted() { for (int i = 1; i < size(); i++) if (keys[i].compareTo(keys[i-1]) < 0) return false; return true; } // check that rank(select(i)) = i private boolean rankCheck() { for (int i = 0; i < size(); i++) if (i != rank(select(i))) return false; for (int i = 0; i < size(); i++) if (keys[i].compareTo(select(rank(keys[i]))) != 0) return false; return true; } public static void main(String[] args) { BinarySearchST<String, Integer> st = new BinarySearchST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); } }
三.二叉查找树
package search; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import java.util.NoSuchElementException; public class BST<Key extends Comparable<Key>, Value> { private Node root; // root of BST private class Node { private Key key; // sorted by key private Value val; // associated data private Node left, right; // left and right subtrees private int size; // number of nodes in subtree public Node(Key key, Value val, int size) { this.key = key; this.val = val; this.size = size; } } public BST() { } public boolean isEmpty() { return size() == 0; } public int size() { return size(root); } // return number of key-value pairs in BST rooted at x private int size(Node x) { if (x == null) return 0; else return x.size; } //判断是否存在key public boolean contains(Key key) { if (key == null) throw new IllegalArgumentException("argument to contains() is null"); return get(key) != null; } //得到key对应的值 public Value get(Key key) { return get(root, key); } private Value get(Node x, Key key) { if (key == null) throw new IllegalArgumentException("calls get() with a null key"); if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp < 0) return get(x.left, key); else if (cmp > 0) return get(x.right, key); else return x.val; } //新增键值对 public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("calls put() with a null key"); if (val == null) { delete(key); return; } root = put(root, key, val); assert check(); } private Node put(Node x, Key key, Value val) { if (x == null) return new Node(key, val, 1); int cmp = key.compareTo(x.key); if (cmp < 0) x.left = put(x.left, key, val); else if (cmp > 0) x.right = put(x.right, key, val); else x.val = val; x.size = 1 + size(x.left) + size(x.right); return x; } //删除最小值 public void deleteMin() { if (isEmpty()) throw new NoSuchElementException("Symbol table underflow"); root = deleteMin(root); assert check(); } private Node deleteMin(Node x) { if (x.left == null) return x.right; x.left = deleteMin(x.left); x.size = size(x.left) + size(x.right) + 1; return x; } //删除最大值 public void deleteMax() { if (isEmpty()) throw new NoSuchElementException("Symbol table underflow"); root = deleteMax(root); assert check(); } private Node deleteMax(Node x) { if (x.right == null) return x.left; x.right = deleteMax(x.right); x.size = size(x.left) + size(x.right) + 1; return x; } //删除操作 public void delete(Key key) { if (key == null) throw new IllegalArgumentException("calls delete() with a null key"); root = delete(root, key); assert check(); } private Node delete(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp < 0) x.left = delete(x.left, key); else if (cmp > 0) x.right = delete(x.right, key); else { if (x.right == null) return x.left; if (x.left == null) return x.right; Node t = x; x = min(t.right); x.right = deleteMin(t.right); x.left = t.left; } x.size = size(x.left) + size(x.right) + 1; return x; } public Key min() { if (isEmpty()) throw new NoSuchElementException("calls min() with empty symbol table"); return min(root).key; } private Node min(Node x) { if (x.left == null) return x; else return min(x.left); } public Key max() { if (isEmpty()) throw new NoSuchElementException("calls max() with empty symbol table"); return max(root).key; } private Node max(Node x) { if (x.right == null) return x; else return max(x.right); } //向下取整 public Key floor(Key key) { if (key == null) throw new IllegalArgumentException("argument to floor() is null"); if (isEmpty()) throw new NoSuchElementException("calls floor() with empty symbol table"); Node x = floor(root, key); if (x == null) throw new NoSuchElementException("argument to floor() is too small"); else return x.key; } private Node floor(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp == 0) return x; if (cmp < 0) return floor(x.left, key); Node t = floor(x.right, key); if (t != null) return t; else return x; } public Key floor2(Key key) { Key x = floor2(root, key, null); if (x == null) throw new NoSuchElementException("argument to floor() is too small"); else return x; } private Key floor2(Node x, Key key, Key best) { if (x == null) return best; int cmp = key.compareTo(x.key); if (cmp < 0) return floor2(x.left, key, best); else if (cmp > 0) return floor2(x.right, key, x.key); else return x.key; } //向上取整 public Key ceiling(Key key) { if (key == null) throw new IllegalArgumentException("argument to ceiling() is null"); if (isEmpty()) throw new NoSuchElementException("calls ceiling() with empty symbol table"); Node x = ceiling(root, key); if (x == null) throw new NoSuchElementException("argument to floor() is too large"); else return x.key; } private Node ceiling(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp == 0) return x; if (cmp < 0) { Node t = ceiling(x.left, key); if (t != null) return t; else return x; } return ceiling(x.right, key); } public Key select(int k) { if (k < 0 || k >= size()) { throw new IllegalArgumentException("argument to select() is invalid: " + k); } Node x = select(root, k); return x.key; } // Return key of rank k. private Node select(Node x, int k) { if (x == null) return null; int t = size(x.left); if (t > k) return select(x.left, k); else if (t < k) return select(x.right, k-t-1); else return x; } //返回小于key的数量 public int rank(Key key) { if (key == null) throw new IllegalArgumentException("argument to rank() is null"); return rank(key, root); } private int rank(Key key, Node x) { if (x == null) return 0; int cmp = key.compareTo(x.key); if (cmp < 0) return rank(key, x.left); else if (cmp > 0) return 1 + size(x.left) + rank(key, x.right); else return size(x.left); } public Iterable<Key> keys() { if (isEmpty()) return new Queue<Key>(); return keys(min(), max()); } public Iterable<Key> keys(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to keys() is null"); if (hi == null) throw new IllegalArgumentException("second argument to keys() is null"); Queue<Key> queue = new Queue<Key>(); keys(root, queue, lo, hi); return queue; } private void keys(Node x, Queue<Key> queue, Key lo, Key hi) { if (x == null) return; int cmplo = lo.compareTo(x.key); int cmphi = hi.compareTo(x.key); if (cmplo < 0) keys(x.left, queue, lo, hi); if (cmplo <= 0 && cmphi >= 0) queue.enqueue(x.key); if (cmphi > 0) keys(x.right, queue, lo, hi); } public int size(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to size() is null"); if (hi == null) throw new IllegalArgumentException("second argument to size() is null"); if (lo.compareTo(hi) > 0) return 0; if (contains(hi)) return rank(hi) - rank(lo) + 1; else return rank(hi) - rank(lo); } //返回树的高度 public int height() { return height(root); } private int height(Node x) { if (x == null) return -1; return 1 + Math.max(height(x.left), height(x.right)); } public Iterable<Key> levelOrder() { Queue<Key> keys = new Queue<Key>(); Queue<Node> queue = new Queue<Node>(); queue.enqueue(root); while (!queue.isEmpty()) { Node x = queue.dequeue(); if (x == null) continue; keys.enqueue(x.key); queue.enqueue(x.left); queue.enqueue(x.right); } return keys; } private boolean check() { if (!isBST()) StdOut.println("Not in symmetric order"); if (!isSizeConsistent()) StdOut.println("Subtree counts not consistent"); if (!isRankConsistent()) StdOut.println("Ranks not consistent"); return isBST() && isSizeConsistent() && isRankConsistent(); } // does this binary tree satisfy symmetric order? // Note: this test also ensures that data structure is a binary tree since order is strict private boolean isBST() { return isBST(root, null, null); } // is the tree rooted at x a BST with all keys strictly between min and max // (if min or max is null, treat as empty constraint) // Credit: Bob Dondero's elegant solution private boolean isBST(Node x, Key min, Key max) { if (x == null) return true; if (min != null && x.key.compareTo(min) <= 0) return false; if (max != null && x.key.compareTo(max) >= 0) return false; return isBST(x.left, min, x.key) && isBST(x.right, x.key, max); } // are the size fields correct? private boolean isSizeConsistent() { return isSizeConsistent(root); } private boolean isSizeConsistent(Node x) { if (x == null) return true; if (x.size != size(x.left) + size(x.right) + 1) return false; return isSizeConsistent(x.left) && isSizeConsistent(x.right); } // check that ranks are consistent private boolean isRankConsistent() { for (int i = 0; i < size(); i++) if (i != rank(select(i))) return false; for (Key key : keys()) if (key.compareTo(select(rank(key))) != 0) return false; return true; } public static void main(String[] args) { BST<String, Integer> st = new BST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } for (String s : st.levelOrder()) StdOut.println(s + " " + st.get(s)); StdOut.println(); for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); } }
四.红黑树
package sort; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; import java.util.NoSuchElementException; public class RedBlackBST<Key extends Comparable<Key>, Value> { private static final boolean RED = true; private static final boolean BLACK = false; private Node root; // root of the BST private class Node { private Key key; // key private Value val; // associated data private Node left, right; // links to left and right subtrees private boolean color; // color of parent link private int size; // subtree count public Node(Key key, Value val, boolean color, int size) { this.key = key; this.val = val; this.color = color; this.size = size; } } public RedBlackBST() { } /*************************************************************************** * Node helper methods. ***************************************************************************/ // is node x red; false if x is null ? private boolean isRed(Node x) { if (x == null) return false; return x.color == RED; } private int size(Node x) { if (x == null) return 0; return x.size; } /** * Returns the number of key-value pairs in this symbol table. * @return the number of key-value pairs in this symbol table */ public int size() { return size(root); } public boolean isEmpty() { return root == null; } /*************************************************************************** * Standard BST search. ***************************************************************************/ /** * Returns the value associated with the given key. * @param key the key * @return the value associated with the given key if the key is in the symbol table * and {@code null} if the key is not in the symbol table * @throws IllegalArgumentException if {@code key} is {@code null} */ public Value get(Key key) { if (key == null) throw new IllegalArgumentException("argument to get() is null"); return get(root, key); } // value associated with the given key in subtree rooted at x; null if no such key private Value get(Node x, Key key) { while (x != null) { int cmp = key.compareTo(x.key); if (cmp < 0) x = x.left; else if (cmp > 0) x = x.right; else return x.val; } return null; } /** * Does this symbol table contain the given key? * @param key the key * @return {@code true} if this symbol table contains {@code key} and * {@code false} otherwise * @throws IllegalArgumentException if {@code key} is {@code null} */ public boolean contains(Key key) { return get(key) != null; } /*************************************************************************** * Red-black tree insertion. ***************************************************************************/ /** * Inserts the specified key-value pair into the symbol table, overwriting the old * value with the new value if the symbol table already contains the specified key. * Deletes the specified key (and its associated value) from this symbol table * if the specified value is {@code null}. * * @param key the key * @param val the value * @throws IllegalArgumentException if {@code key} is {@code null} */ public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("first argument to put() is null"); if (val == null) { delete(key); return; } root = put(root, key, val); root.color = BLACK; // assert check(); } // insert the key-value pair in the subtree rooted at h private Node put(Node h, Key key, Value val) { if (h == null) return new Node(key, val, RED, 1); int cmp = key.compareTo(h.key); if (cmp < 0) h.left = put(h.left, key, val); else if (cmp > 0) h.right = put(h.right, key, val); else h.val = val; // fix-up any right-leaning links if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h); if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h); if (isRed(h.left) && isRed(h.right)) flipColors(h); h.size = size(h.left) + size(h.right) + 1; return h; } /*************************************************************************** * Red-black tree deletion. ***************************************************************************/ /** * Removes the smallest key and associated value from the symbol table. * @throws NoSuchElementException if the symbol table is empty */ public void deleteMin() { if (isEmpty()) throw new NoSuchElementException("BST underflow"); // if both children of root are black, set root to red if (!isRed(root.left) && !isRed(root.right)) root.color = RED; root = deleteMin(root); if (!isEmpty()) root.color = BLACK; // assert check(); } // delete the key-value pair with the minimum key rooted at h private Node deleteMin(Node h) { if (h.left == null) return null; if (!isRed(h.left) && !isRed(h.left.left)) h = moveRedLeft(h); h.left = deleteMin(h.left); return balance(h); } /** * Removes the largest key and associated value from the symbol table. * @throws NoSuchElementException if the symbol table is empty */ public void deleteMax() { if (isEmpty()) throw new NoSuchElementException("BST underflow"); // if both children of root are black, set root to red if (!isRed(root.left) && !isRed(root.right)) root.color = RED; root = deleteMax(root); if (!isEmpty()) root.color = BLACK; // assert check(); } // delete the key-value pair with the maximum key rooted at h private Node deleteMax(Node h) { if (isRed(h.left)) h = rotateRight(h); if (h.right == null) return null; if (!isRed(h.right) && !isRed(h.right.left)) h = moveRedRight(h); h.right = deleteMax(h.right); return balance(h); } /** * Removes the specified key and its associated value from this symbol table * (if the key is in this symbol table). * * @param key the key * @throws IllegalArgumentException if {@code key} is {@code null} */ public void delete(Key key) { if (key == null) throw new IllegalArgumentException("argument to delete() is null"); if (!contains(key)) return; // if both children of root are black, set root to red if (!isRed(root.left) && !isRed(root.right)) root.color = RED; root = delete(root, key); if (!isEmpty()) root.color = BLACK; // assert check(); } // delete the key-value pair with the given key rooted at h private Node delete(Node h, Key key) { // assert get(h, key) != null; if (key.compareTo(h.key) < 0) { if (!isRed(h.left) && !isRed(h.left.left)) h = moveRedLeft(h); h.left = delete(h.left, key); } else { if (isRed(h.left)) h = rotateRight(h); if (key.compareTo(h.key) == 0 && (h.right == null)) return null; if (!isRed(h.right) && !isRed(h.right.left)) h = moveRedRight(h); if (key.compareTo(h.key) == 0) { Node x = min(h.right); h.key = x.key; h.val = x.val; // h.val = get(h.right, min(h.right).key); // h.key = min(h.right).key; h.right = deleteMin(h.right); } else h.right = delete(h.right, key); } return balance(h); } /*************************************************************************** * Red-black tree helper functions. ***************************************************************************/ // make a left-leaning link lean to the right private Node rotateRight(Node h) { // assert (h != null) && isRed(h.left); Node x = h.left; h.left = x.right; x.right = h; x.color = x.right.color; x.right.color = RED; x.size = h.size; h.size = size(h.left) + size(h.right) + 1; return x; } // make a right-leaning link lean to the left private Node rotateLeft(Node h) { // assert (h != null) && isRed(h.right); Node x = h.right; h.right = x.left; x.left = h; x.color = x.left.color; x.left.color = RED; x.size = h.size; h.size = size(h.left) + size(h.right) + 1; return x; } // flip the colors of a node and its two children private void flipColors(Node h) { // h must have opposite color of its two children // assert (h != null) && (h.left != null) && (h.right != null); // assert (!isRed(h) && isRed(h.left) && isRed(h.right)) // || (isRed(h) && !isRed(h.left) && !isRed(h.right)); h.color = !h.color; h.left.color = !h.left.color; h.right.color = !h.right.color; } // Assuming that h is red and both h.left and h.left.left // are black, make h.left or one of its children red. private Node moveRedLeft(Node h) { // assert (h != null); // assert isRed(h) && !isRed(h.left) && !isRed(h.left.left); flipColors(h); if (isRed(h.right.left)) { h.right = rotateRight(h.right); h = rotateLeft(h); flipColors(h); } return h; } // Assuming that h is red and both h.right and h.right.left // are black, make h.right or one of its children red. private Node moveRedRight(Node h) { // assert (h != null); // assert isRed(h) && !isRed(h.right) && !isRed(h.right.left); flipColors(h); if (isRed(h.left.left)) { h = rotateRight(h); flipColors(h); } return h; } // restore red-black tree invariant private Node balance(Node h) { // assert (h != null); if (isRed(h.right)) h = rotateLeft(h); if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h); if (isRed(h.left) && isRed(h.right)) flipColors(h); h.size = size(h.left) + size(h.right) + 1; return h; } /*************************************************************************** * Utility functions. ***************************************************************************/ /** * Returns the height of the BST (for debugging). * @return the height of the BST (a 1-node tree has height 0) */ public int height() { return height(root); } private int height(Node x) { if (x == null) return -1; return 1 + Math.max(height(x.left), height(x.right)); } /*************************************************************************** * Ordered symbol table methods. ***************************************************************************/ /** * Returns the smallest key in the symbol table. * @return the smallest key in the symbol table * @throws NoSuchElementException if the symbol table is empty */ public Key min() { if (isEmpty()) throw new NoSuchElementException("calls min() with empty symbol table"); return min(root).key; } // the smallest key in subtree rooted at x; null if no such key private Node min(Node x) { // assert x != null; if (x.left == null) return x; else return min(x.left); } /** * Returns the largest key in the symbol table. * @return the largest key in the symbol table * @throws NoSuchElementException if the symbol table is empty */ public Key max() { if (isEmpty()) throw new NoSuchElementException("calls max() with empty symbol table"); return max(root).key; } // the largest key in the subtree rooted at x; null if no such key private Node max(Node x) { // assert x != null; if (x.right == null) return x; else return max(x.right); } /** * Returns the largest key in the symbol table less than or equal to {@code key}. * @param key the key * @return the largest key in the symbol table less than or equal to {@code key} * @throws NoSuchElementException if there is no such key * @throws IllegalArgumentException if {@code key} is {@code null} */ public Key floor(Key key) { if (key == null) throw new IllegalArgumentException("argument to floor() is null"); if (isEmpty()) throw new NoSuchElementException("calls floor() with empty symbol table"); Node x = floor(root, key); if (x == null) throw new NoSuchElementException("argument to floor() is too small"); else return x.key; } // the largest key in the subtree rooted at x less than or equal to the given key private Node floor(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp == 0) return x; if (cmp < 0) return floor(x.left, key); Node t = floor(x.right, key); if (t != null) return t; else return x; } /** * Returns the smallest key in the symbol table greater than or equal to {@code key}. * @param key the key * @return the smallest key in the symbol table greater than or equal to {@code key} * @throws NoSuchElementException if there is no such key * @throws IllegalArgumentException if {@code key} is {@code null} */ public Key ceiling(Key key) { if (key == null) throw new IllegalArgumentException("argument to ceiling() is null"); if (isEmpty()) throw new NoSuchElementException("calls ceiling() with empty symbol table"); Node x = ceiling(root, key); if (x == null) throw new NoSuchElementException("argument to ceiling() is too small"); else return x.key; } // the smallest key in the subtree rooted at x greater than or equal to the given key private Node ceiling(Node x, Key key) { if (x == null) return null; int cmp = key.compareTo(x.key); if (cmp == 0) return x; if (cmp > 0) return ceiling(x.right, key); Node t = ceiling(x.left, key); if (t != null) return t; else return x; } /** * Return the key in the symbol table whose rank is {@code k}. * This is the (k+1)st smallest key in the symbol table. * * @param k the order statistic * @return the key in the symbol table of rank {@code k} * @throws IllegalArgumentException unless {@code k} is between 0 and * <em>n</em>–1 */ public Key select(int k) { if (k < 0 || k >= size()) { throw new IllegalArgumentException("argument to select() is invalid: " + k); } Node x = select(root, k); return x.key; } // the key of rank k in the subtree rooted at x private Node select(Node x, int k) { // assert x != null; // assert k >= 0 && k < size(x); int t = size(x.left); if (t > k) return select(x.left, k); else if (t < k) return select(x.right, k-t-1); else return x; } /** * Return the number of keys in the symbol table strictly less than {@code key}. * @param key the key * @return the number of keys in the symbol table strictly less than {@code key} * @throws IllegalArgumentException if {@code key} is {@code null} */ public int rank(Key key) { if (key == null) throw new IllegalArgumentException("argument to rank() is null"); return rank(key, root); } // number of keys less than key in the subtree rooted at x private int rank(Key key, Node x) { if (x == null) return 0; int cmp = key.compareTo(x.key); if (cmp < 0) return rank(key, x.left); else if (cmp > 0) return 1 + size(x.left) + rank(key, x.right); else return size(x.left); } /*************************************************************************** * Range count and range search. ***************************************************************************/ /** * Returns all keys in the symbol table as an {@code Iterable}. * To iterate over all of the keys in the symbol table named {@code st}, * use the foreach notation: {@code for (Key key : st.keys())}. * @return all keys in the symbol table as an {@code Iterable} */ public Iterable<Key> keys() { if (isEmpty()) return new Queue<Key>(); return keys(min(), max()); } /** * Returns all keys in the symbol table in the given range, * as an {@code Iterable}. * * @param lo minimum endpoint * @param hi maximum endpoint * @return all keys in the symbol table between {@code lo} * (inclusive) and {@code hi} (inclusive) as an {@code Iterable} * @throws IllegalArgumentException if either {@code lo} or {@code hi} * is {@code null} */ public Iterable<Key> keys(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to keys() is null"); if (hi == null) throw new IllegalArgumentException("second argument to keys() is null"); Queue<Key> queue = new Queue<Key>(); // if (isEmpty() || lo.compareTo(hi) > 0) return queue; keys(root, queue, lo, hi); return queue; } // add the keys between lo and hi in the subtree rooted at x // to the queue private void keys(Node x, Queue<Key> queue, Key lo, Key hi) { if (x == null) return; int cmplo = lo.compareTo(x.key); int cmphi = hi.compareTo(x.key); if (cmplo < 0) keys(x.left, queue, lo, hi); if (cmplo <= 0 && cmphi >= 0) queue.enqueue(x.key); if (cmphi > 0) keys(x.right, queue, lo, hi); } /** * Returns the number of keys in the symbol table in the given range. * * @param lo minimum endpoint * @param hi maximum endpoint * @return the number of keys in the symbol table between {@code lo} * (inclusive) and {@code hi} (inclusive) * @throws IllegalArgumentException if either {@code lo} or {@code hi} * is {@code null} */ public int size(Key lo, Key hi) { if (lo == null) throw new IllegalArgumentException("first argument to size() is null"); if (hi == null) throw new IllegalArgumentException("second argument to size() is null"); if (lo.compareTo(hi) > 0) return 0; if (contains(hi)) return rank(hi) - rank(lo) + 1; else return rank(hi) - rank(lo); } /*************************************************************************** * Check integrity of red-black tree data structure. ***************************************************************************/ private boolean check() { if (!isBST()) StdOut.println("Not in symmetric order"); if (!isSizeConsistent()) StdOut.println("Subtree counts not consistent"); if (!isRankConsistent()) StdOut.println("Ranks not consistent"); if (!is23()) StdOut.println("Not a 2-3 tree"); if (!isBalanced()) StdOut.println("Not balanced"); return isBST() && isSizeConsistent() && isRankConsistent() && is23() && isBalanced(); } // does this binary tree satisfy symmetric order? // Note: this test also ensures that data structure is a binary tree since order is strict private boolean isBST() { return isBST(root, null, null); } // is the tree rooted at x a BST with all keys strictly between min and max // (if min or max is null, treat as empty constraint) // Credit: Bob Dondero's elegant solution private boolean isBST(Node x, Key min, Key max) { if (x == null) return true; if (min != null && x.key.compareTo(min) <= 0) return false; if (max != null && x.key.compareTo(max) >= 0) return false; return isBST(x.left, min, x.key) && isBST(x.right, x.key, max); } // are the size fields correct? private boolean isSizeConsistent() { return isSizeConsistent(root); } private boolean isSizeConsistent(Node x) { if (x == null) return true; if (x.size != size(x.left) + size(x.right) + 1) return false; return isSizeConsistent(x.left) && isSizeConsistent(x.right); } // check that ranks are consistent private boolean isRankConsistent() { for (int i = 0; i < size(); i++) if (i != rank(select(i))) return false; for (Key key : keys()) if (key.compareTo(select(rank(key))) != 0) return false; return true; } // Does the tree have no red right links, and at most one (left) // red links in a row on any path? private boolean is23() { return is23(root); } private boolean is23(Node x) { if (x == null) return true; if (isRed(x.right)) return false; if (x != root && isRed(x) && isRed(x.left)) return false; return is23(x.left) && is23(x.right); } // do all paths from root to leaf have same number of black edges? private boolean isBalanced() { int black = 0; // number of black links on path from root to min Node x = root; while (x != null) { if (!isRed(x)) black++; x = x.left; } return isBalanced(root, black); } // does every path from the root to a leaf have the given number of black links? private boolean isBalanced(Node x, int black) { if (x == null) return black == 0; if (!isRed(x)) black--; return isBalanced(x.left, black) && isBalanced(x.right, black); } public static void main(String[] args) { RedBlackBST<String, Integer> st = new RedBlackBST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } StdOut.println(); for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); StdOut.println(); } }
五.散列表
1.基于拉链法的散列表
package search; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class SeparateChainingHashST<Key, Value> { private static final int INIT_CAPACITY = 4; private int n; // number of key-value pairs private int m; // hash table size private SequentialSearchST<Key, Value>[] st; // array of linked-list symbol tables public SeparateChainingHashST() { this(INIT_CAPACITY); } public SeparateChainingHashST(int m) { this.m = m; st = (SequentialSearchST<Key, Value>[]) new SequentialSearchST[m]; for (int i = 0; i < m; i++) st[i] = new SequentialSearchST<Key, Value>(); } private void resize(int chains) { SeparateChainingHashST<Key, Value> temp = new SeparateChainingHashST<Key, Value>(chains); for (int i = 0; i < m; i++) { for (Key key : st[i].keys()) { temp.put(key, st[i].get(key)); } } this.m = temp.m; this.n = temp.n; this.st = temp.st; } private int hash(Key key) { return (key.hashCode() & 0x7fffffff) % m; } public int size() { return n; } public boolean isEmpty() { return size() == 0; } public boolean contains(Key key) { if (key == null) throw new IllegalArgumentException("argument to contains() is null"); return get(key) != null; } public Value get(Key key) { if (key == null) throw new IllegalArgumentException("argument to get() is null"); int i = hash(key); return st[i].get(key); } public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("first argument to put() is null"); if (val == null) { delete(key); return; } // double table size if average length of list >= 10 if (n >= 10*m) resize(2*m); int i = hash(key); if (!st[i].contains(key)) n++; st[i].put(key, val); } public void delete(Key key) { if (key == null) throw new IllegalArgumentException("argument to delete() is null"); int i = hash(key); if (st[i].contains(key)) n--; st[i].delete(key); // halve table size if average length of list <= 2 if (m > INIT_CAPACITY && n <= 2*m) resize(m/2); } public Iterable<Key> keys() { Queue<Key> queue = new Queue<Key>(); for (int i = 0; i < m; i++) { for (Key key : st[i].keys()) queue.enqueue(key); } return queue; } public static void main(String[] args) { SeparateChainingHashST<String, Integer> st = new SeparateChainingHashST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); } }
2.基于线性探测法的散列表
package search; import edu.princeton.cs.algs4.Queue; import edu.princeton.cs.algs4.StdIn; import edu.princeton.cs.algs4.StdOut; public class LinearProbingHashST<Key, Value> { private static final int INIT_CAPACITY = 4; private int n; // number of key-value pairs in the symbol table private int m; // size of linear probing table private Key[] keys; // the keys private Value[] vals; // the values public LinearProbingHashST() { this(INIT_CAPACITY); } public LinearProbingHashST(int capacity) { m = capacity; n = 0; keys = (Key[]) new Object[m]; vals = (Value[]) new Object[m]; } public int size() { return n; } public boolean isEmpty() { return size() == 0; } public boolean contains(Key key) { if (key == null) throw new IllegalArgumentException("argument to contains() is null"); return get(key) != null; } private int hash(Key key) { return (key.hashCode() & 0x7fffffff) % m; } private void resize(int capacity) { LinearProbingHashST<Key, Value> temp = new LinearProbingHashST<Key, Value>(capacity); for (int i = 0; i < m; i++) { if (keys[i] != null) { temp.put(keys[i], vals[i]); } } keys = temp.keys; vals = temp.vals; m = temp.m; } public void put(Key key, Value val) { if (key == null) throw new IllegalArgumentException("first argument to put() is null"); if (val == null) { delete(key); return; } // double table size if 50% full if (n >= m/2) resize(2*m); int i; for (i = hash(key); keys[i] != null; i = (i + 1) % m) { if (keys[i].equals(key)) { vals[i] = val; return; } } keys[i] = key; vals[i] = val; n++; } public Value get(Key key) { if (key == null) throw new IllegalArgumentException("argument to get() is null"); for (int i = hash(key); keys[i] != null; i = (i + 1) % m) if (keys[i].equals(key)) return vals[i]; return null; } public void delete(Key key) { if (key == null) throw new IllegalArgumentException("argument to delete() is null"); if (!contains(key)) return; // find position i of key int i = hash(key); while (!key.equals(keys[i])) { i = (i + 1) % m; } // delete key and associated value keys[i] = null; vals[i] = null; // rehash all keys in same cluster i = (i + 1) % m; while (keys[i] != null) { // delete keys[i] an vals[i] and reinsert Key keyToRehash = keys[i]; Value valToRehash = vals[i]; keys[i] = null; vals[i] = null; n--; put(keyToRehash, valToRehash); i = (i + 1) % m; } n--; // halves size of array if it's 12.5% full or less if (n > 0 && n <= m/8) resize(m/2); assert check(); } public Iterable<Key> keys() { Queue<Key> queue = new Queue<Key>(); for (int i = 0; i < m; i++) if (keys[i] != null) queue.enqueue(keys[i]); return queue; } private boolean check() { // check that hash table is at most 50% full if (m < 2*n) { System.err.println("Hash table size m = " + m + "; array size n = " + n); return false; } // check that each key in table can be found by get() for (int i = 0; i < m; i++) { if (keys[i] == null) continue; else if (get(keys[i]) != vals[i]) { System.err.println("get[" + keys[i] + "] = " + get(keys[i]) + "; vals[i] = " + vals[i]); return false; } } return true; } public static void main(String[] args) { LinearProbingHashST<String, Integer> st = new LinearProbingHashST<String, Integer>(); for (int i = 0; !StdIn.isEmpty(); i++) { String key = StdIn.readString(); st.put(key, i); } // print keys for (String s : st.keys()) StdOut.println(s + " " + st.get(s)); } }