一、二叉树
1. 定义
二叉树的每个节点最多只有两棵子树,且子树有左右之分,次序不能颠倒。
2. 几种特殊的二叉树
(1)满二叉树(完美二叉树):所有非叶子节点均有两个子节点,所有叶子节点必须在同一层上。节点数达到最大值。

(2)完全二叉树:若设二叉树的深度为h,除第h层外,其它各层的节点数都达到最大值,第h层所有的节点都连续集中在最左边。
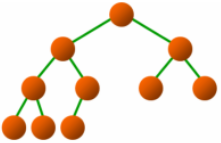
(3)完满二叉树:所有非叶子节点的度都是2。

二、二叉排序树
1. 定义
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有节点的值均小于它的根节点的值;
(2)若有子树不空,则有子树上所有节点的值均大于或等于它的根节点的值;
(3)左、右子树也分别为二叉排序树;
(4)没有键值相等的节点。
2. 特性
对二叉排序树进行中序遍历,即可得到有序的数列。
3. 应用
可用于数据查找,其时间复杂度与二分查找一样。
二叉排序树的高度决定了二叉排序树的查找效率。
三、平衡二叉树
1. 为什么需要平衡二叉树
在某些极端情况下,二叉排序树将退化成近似链或链,其操作的时间复杂度将退化成线性的,为了防止这种情况的出现,需要使用某种算法来维持二叉排序树的平衡性,于是便有了平衡二叉树。
2. 定义
平衡二叉树又被称为AVL树,且有以下性质:它是一棵空树或它的左右两棵子树的高度差的绝对值不超过1,并且左右两棵子树都是一棵平衡二叉树。
3. 算法
平衡二叉树的常用算法有AVL树、红黑树等。
(1)AVL树
AVL树是严格的平衡二叉树,执行插入删除操作时,只要不满足AVL树的条件,就要通过旋转来保持平衡。在AVL树中任何节点的两棵子树的高度最大差别为1,所以AVL树也被称为高度平衡树。查找操作很快,但是插入和删除操作可能都需要消耗一定时间用于树旋转。适用于插入删除次数少,查找多的情况。
(2)红黑树
红黑树是非严格的平衡二叉树,用非严格的平衡来换取增删节点时旋转次数的降低,任何不平衡都会在三次旋转之内解决。查询性能略逊于AVL树,但增删操作比AVL树强很多,应用场景更多,典型的用途是实现关联数组。