题目
标题:等差素数列
2,3,5,7,11,13,....是素数序列。
类似:7,37,67,97,127,157 这样完全由素数组成的等差数列,叫等差素数数列。
上边的数列公差为30,长度为6。
2004年,格林与华人陶哲轩合作证明了:存在任意长度的素数等差数列。
这是数论领域一项惊人的成果!
有这一理论为基础,请你借助手中的计算机,满怀信心地搜索:
长度为10的等差素数列,其公差最小值是多少?
注意:需要提交的是一个整数,不要填写任何多余的内容和说明文字。
题解
絮絮叨叨(骂骂咧咧
一开始看到这道题还是有点懵的,毕竟我个数学小白,对素数什么的最发怵了。
然后找了好多大佬的题解都没看明白,甚至有一个大佬的代码看的我晕头转向~
然后终于被我找到一份能看懂并且觉得非常正确的代码,思路如下:
思路
两层循环,一层循环用于循环公差,一层循环用于循环起始素数。
需要注意的是,内层循环起始素数的时候,不能无边界循环下去,要设置一个上限,否则外层循环永远无法走到下一个公差(自己写的时候自以为是犯的错
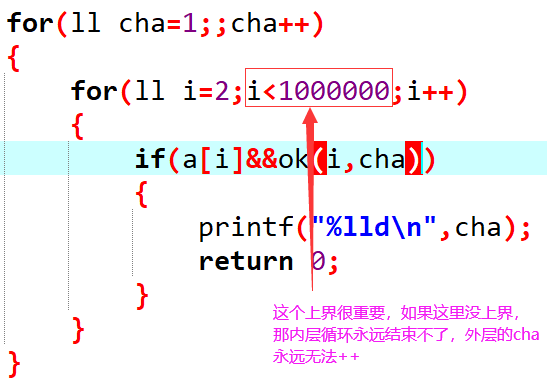
内层循环走的时候,只需要判断:
①这个数是不是素数(作为起始素数最基本的条件)
②判断从这个素数开始,以cha为公差能否存在连续10个等差的素数。【用ok函数来判断的】
如果以上两个条件都满足,则这就是我们要找的长度为10的等差素数列,其公差的最小值
因为我们是从小到大找的,那我们找到的满足条件的第一个就是答案~
代码
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn=1e6+50;
ll a[maxn];
bool ok(ll n,ll cha)
{
for(ll i=0;i<10;i++)
{
if(!a[n+i*cha])return 0;
}
return 1;
}
int main()
{
a[1]=0;
a[2]=1;
a[3]=1;
for(ll i=4;i<=1000000;i++)
{
bool flag=0;
for(ll j=2;j*j<=i;j++)
{
if(i%j==0)
{
flag=1;
break;
}
}
if(flag)a[i]=0;
else a[i]=1;
}
for(ll cha=1;;cha++)
{
for(ll i=2;i<1000000;i++)
{
if(a[i]&&ok(i,cha))
{
printf("%lld
",cha);
return 0;
}
}
}
}
后记
其实我对素数一直都怀有敬畏之心,希望能找个时间把素数的相关算法摸摸透,把板子整理齐全~(先给自己挖个坑
要是整理好了,我就把链接更新上来!(咕咕咕~