学习总结 -- 汉诺塔问题

前言：永远记住只学不总结等于白学

背景：之前在老师发的题上看到了有关汉诺塔问题的时间复杂度，然后忘记怎么实现了，therefore，今天又看了看~

问题：汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

haha，想了解的朋友，可以玩玩网页版的汉诺塔游戏找找感觉

刚看这道题时有点懵，没有思路不知怎样下手，感觉随便移动，找不到规律。

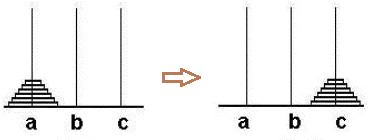
但是请想：（这点很关键）逆向思维，现在你已经成功将63个盘子移动到b柱了，现在只剩下最后一步将 a柱的最大的盘子 移到 c 处。党最大的盘子由a移动到c后，b上是余下的63个盘子，a为空。现在的目标就变成了将这63个盘子由b移动到c。这和之前的思路是一样的，只是由a柱变为了b柱，规模由64变为了63。因此采用相同的方法，将62个盘子由b 移动到a，再将最下面的盘子移到c........

一般规律（我们可以把最底下的盘子和上面的所有盘子分别看成一体）：

1：将b柱子作为辅助，把a上的63个圆盘移动到b上

2：将a 上最后一个圆盘移动到c

3：将a作为辅助，把b 上的62个圆盘移动到a上

4：将b上最后一个圆盘移动到c上

5：。。。

关键代码：

void Hanoi(char src, char des, char via, int n)
      {
          Hanoi(src, via, des, n - 1);
          Move(src, des, n); //把第n个盘子直接从src移动到des
          Hanoi(via,des, src, n - 1);
      }

　再来说说时间复杂度

f(1) = 1 , f(2) = 3 , f(3) = 7....(这是根据问题规模不断增大时，所需的步数)

由此可得f[n] = 2f[n-1] + 1;经推导 可以得出f(x) = 2的n 次方 -1；