POJ2488 深度优先搜索+回溯

POJ2488

题目

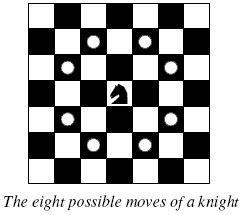
　　骑士按照下图所示的走法对棋盘进行巡逻，每个格子只允许巡逻一次，且必须巡逻所有格子。给定棋盘的行数p和列数q，输出一条骑士巡逻路径，若不存在这样一条路径，则输出impossible。

图1 骑士的8种走法 　　骑士巡逻问题的简化版本，是哈密顿路径问题的特殊形式，但是是线性时间内可以解决的$^{[1]}$。

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

算法思路

　　深度优先搜索（Depth-First Search，DFS）算法，伪代码如下(^{[2]})：

图2 DFS算法伪代码 　　DFS算法遍历图会建立一个如图3所示的深度优先搜索树，但是从搜索树中可以看出，原始DFS算法不是我们想要的，我们想要的是每个格子只巡逻一次的DFS算法，也就是说我们需要一个深度为棋盘格子数的搜索树（也即没有分叉的树）。那如何改进呢？我们设置一个计数器cnt用来表示树的深度，假如我们访问节点u时，此时DFS不能进行下去了，我们核验深度是否等于棋盘格子数，若等于，则说明我们找到了所求路径，若不等于，说明我们找的这条路径是不对的，这时我们需要将当前节点重置为未搜索的节点，然后回溯到前一节点，并对前一节点的下一个子节点（即下一个可以巡逻的格子）进行DFS。可以参考代码中的注释进行理解。

图3 深度优先搜索树

　　1个WA点：若存在多条巡逻路径，题目要求输出字典序优先的路径，lexicographically first path。也就是说，假如A1B1C1和A1C1B1都是允许的路径，则选择A1B1C1，因为B在C前面。其实这一点挺好实现，只需要从左往右扫描“列”即可保证字典序优先。

代码

Result: 372kB, 0ms.

#include <stdio.h>
#include <string.h>
#include <vector>

int n, p, q;
int delta_row[8] = { -1, 1, -2, 2, -2, 2, -1, 1 };//DFS的搜索顺序，按照列从左往右的顺序进行搜索。
int delta_col[8] = { -2, -2, -1, -1, 1, 1, 2, 2 };//即搜索的优先级(-1, -2)=(1, -2)>(-2, -1)=(2, -1)>(-2, 1)=(2, 1)>(-1, 2)=(1, 2)，等于的意思是先搜索哪一个不影响字典序
int explored[30][30];//标记是否为已搜索过的节点
int cnt;
struct Node {
	int row, col;
} path[30];//记录下路径

void Init() {
	memset(explored, 0, sizeof(explored));
	cnt = 0;
}

bool Dfs(int row, int col) {
	explored[row][col] = 1;//标记为已搜索的节点
	cnt++;//深度加1
	path[cnt].row = row;
	path[cnt].col = col;
	for (int i = 0; i < 8; i++) {//按照列从左往右的顺序进行搜索
		int row_new = row + delta_row[i], col_new = col + delta_col[i];
		if (row_new >= 1 && row_new <= p && col_new >= 1 && col_new <= q && !explored[row_new][col_new]) {//骑士要去巡逻的新节点(row_new, col_new)在棋盘范围内且未搜索过
			if (Dfs(row_new, col_new))//若找到路径，直接break，一层层跳出递归，若没找到，对下一个优先级的要去巡逻的新节点进行搜索
				break;
		}
	}
	if (cnt == p * q)//若深度为p*q，说明我们找到了路径
		return true;
	else {//若没找到，回溯到前一节点，当前节点置为未搜索的节点，树的深度减1
		explored[row][col] = 0;
		cnt--;
		return false;
	}
}

int main() {
	scanf("%d", &n);
	for (int t = 1; t <= n; t++) {
		scanf("%d %d", &p, &q);
		printf("Scenario #%d:
", t);
		Init();
		if (Dfs(1, 1)) {
			for (int i = 1; i <= p * q; i++)
				printf("%c%c", 'A' + path[i].col - 1, '1' + path[i].row - 1);
			printf("
");
		}
		else
			printf("impossible
");
		if (t != n)
			printf("
");
	}
	return 0;
}

　　最后提一点，本题是要求我们找出路径，所以理论上应该调用程序中的DFS对每个格子进行一次DFS，而不只是对(1, 1)格子调用DFS(1, 1)。但实际上，只调用DFS(1, 1)即可。我猜测是存在这样一个事实的，若大小为(p imes q)（(1le p imes qle 26)）的棋盘格存在符合题意得路径，则至少存在一条从(1, 1)格子开始巡逻的路径。
　　尝试网上查阅一些资料，并没有找到直接证明上述结论的。我们假设上述结论成立，那从(1, 1)开始巡逻的路径正是符合题目要求的字典序优先的路径。
　　关于小于(8 imes 8)的棋盘格的骑士巡逻问题的更多细节，可以参照这篇论文Knight's Tour。

参考：

[1] Wikipedia: Knight's tour
[2] 算法设计