石子归并

 

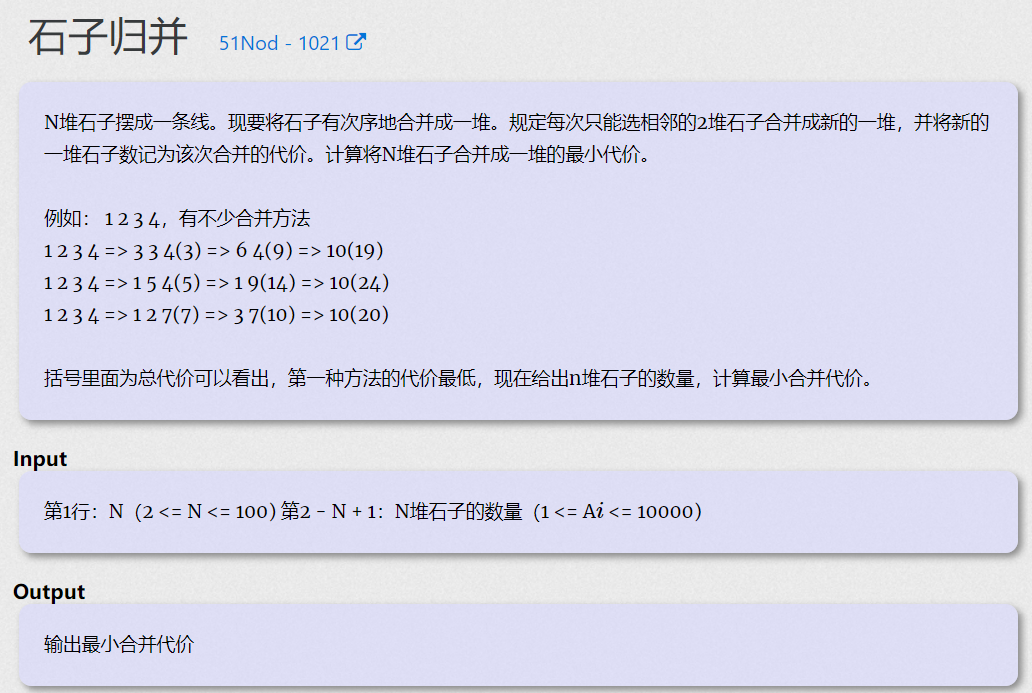
【思路】

 我们 dp[i][j] 来表示合并第 i 堆到第 j 堆石子的最小代价。

 那么状态转移方程为  dp[i][j] = min ( dp[i][j]，dp[i][k]+dp[k+1][j]+w[i][j]);

其中， w[i][j] 表示把两部分合并起来的代价，即从第 i 堆到第 j 堆石子个数的和，为了方便查询，我们可以用 sum[i] 表示从第1堆到第i堆的石子个数和，那么 w[i][j]=sum[j]-sum[i-1].（前缀和思想）

AC_Code:

#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=205;
const ll mod=1e9+7;
const ll INF=1e18;
const double eps = 1e-9;

int n,x;
int sum[maxn];
int dp[maxn][maxn];///合并第i堆到第j堆石子的最小代价
int main()
{
    while(~scanf("%d",&n)){
        sum[0]=0;
        memset(dp,0x3f,sizeof(dp));
        for(int i=1;i<=n;i++){
            scanf("%d",&x);
            sum[i]=sum[i-1]+x;
            dp[i][i]=0;
        }
        for(int len=2;len<=n;len++){
            for(int i=1;i<=n;i++){
                int j=i+len-1;
                if( j>n ) continue;
                for(int k=i;k<j;k++){
                    dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+(sum[j]-sum[i-1]));
                }
            }
        }
        printf("%d
",dp[1][n]);
    }
    return 0;
}

【平行四边形优化】:详解

#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=205;
const ll mod=1e9+7;
const ll INF=1e18;
const double eps = 1e-9;

int n,x;
int sum[maxn];
int dp[maxn][maxn];///合并第i堆到第j堆石子的最小代价
int s[maxn][maxn];
int main()
{
    while(~scanf("%d",&n)){
        sum[0]=0;
        memset(dp,0x3f,sizeof(dp));
        for(int i=1;i<=n;i++){
            scanf("%d",&x);
            sum[i]=sum[i-1]+x;
            dp[i][i]=0;
            s[i][i]=i;
        }
        for(int len=2;len<=n;len++){
            for(int i=1;i<=n;i++){
                int j=i+len-1;
                if( j>n ){
                    continue;
                }
                for(int k=s[i][j-1];k<=s[i+1][j];k++){
                    if( dp[i][k]+dp[k+1][j]+(sum[j]-sum[i-1])<dp[i][j] ){
                        dp[i][j]=dp[i][k]+dp[k+1][j]+(sum[j]-sum[i-1]);
                        s[i][j]=k;
                    }
                }
            }
        }
        printf("%d
",dp[1][n]);
    }
    return 0;
}