图论学习：生成树的Matrix-tree定理

前置知识：矩阵的代数余子式，拉普拉斯矩阵（基尔霍夫矩阵），证明的话还需要用到关联矩阵、柯西——比内公式等

此处刚开始介绍的是没有重边和自环的无向图

1.代数余子式：

2.拉普拉斯矩阵

如：

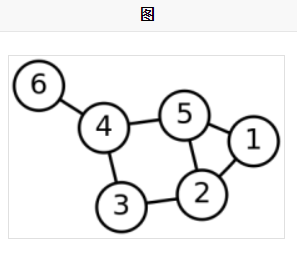
3.矩阵数定理：

无向图的生成树个数就等于这副图的拉普拉斯矩阵的任意一个代数余子式值。

4.拉普拉斯矩阵的性质

定理1：拉普拉斯矩阵的任意一个代数余子式值都相同
定理2：拉普拉斯矩阵的行列式为0

根据定理1，我们只需要证明 ({C}_{1,1})是图的生成树个数就好了。
这里不写具体证明，想要知道的可以去自行了解

5.推广：

6.模板和例题：

1.Highways
模板：求无向图的最小生成树个数（无重边和自环）

点击查看代码块

/*
矩阵树定理：
无向图的生成树个数就等于这副图的拉普拉斯矩阵的任意一个代数余子式值。
*/
#include <bits/stdc++.h>

#define ed end()
#define bg begin()
#define mkp make_pair
#define pb push_back
#define v(T) vector<T>
#define all(x) x.bg,x.ed
#define newline puts("")
#define si(x) ((int)x.size())
#define rep(i,n) for(int i=1;i<=n;++i)
#define rrep(i,n) for(int i=0;i<n;++i)
#define srep(i,s,t) for(int i=s;i<=t;++i)

using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int maxn = 50;
const int inf = 0x7f7f7f7f;
const ll inf_ll = 1ll*inf*inf;
const int Mod = 1e9+7;
const double eps = 1e-7;
int n,m;
int g[maxn][maxn];
ll L[maxn][maxn];

ll det(int n){
    ll ret = 1;
    for (int i=2;i<=n;i++){
        for (int j=i+1;j<=n;j++){
            while(L[j][i]){
                ll tmp=L[i][i]/L[j][i];//不存在除不尽的情况
                for(int k=i;k<=n;k++)
                    L[i][k] -= tmp*L[j][k];
                
                for(int k=i;k<=n;k++)
                    swap(L[i][k],L[j][k]);
                
                ret = -ret;
            }
        }
        if(!L[i][i]) return 0;
        ret *= L[i][i];
    }
    if(ret < 0) ret = -ret;
    return ret;
}
int main(){
    int T;
    scanf("%d",&T);
    for(int _=1;_<=T;_++)
    {
        memset(g,0,sizeof(g));
        memset(L,0,sizeof(L));
        scanf("%d%d",&n,&m);
        rep(i,m){
            int u,v;
            scanf("%d%d",&u,&v);
            g[u][v]=g[v][u]=1;
        }
        for (int i=1;i<=n;i++){
            for (int j=i;j<=n;j++){
                if(g[i][j]){
                    L[i][i]++;L[j][j]++;
                    L[i][j]--;L[j][i]--;
                }
            }
        }
        ll ans = det(n);
        printf("%lld
",ans);
    }
    return 0;
}

2.P6178 【模板】Matrix-Tree 定理

点击查看代码块