给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
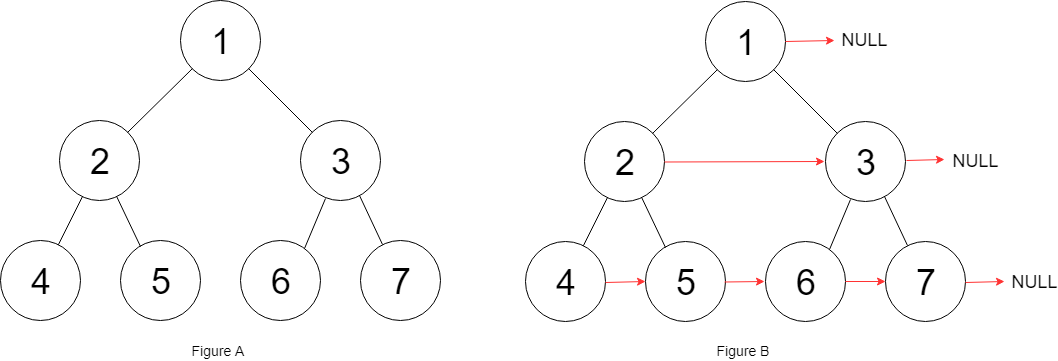
这道题目明显是关于层序遍历的题目,于是我也没想太多,直接套层序遍历的模板,但是还是需要注意一下边界的条件,编码的技巧也没太大的必要说,基本是基于模拟实现的的。
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr)
return nullptr;
// BFS
queue<Node*> que;
que.push(root);
while (!que.empty()){
int n = que.size();
cout<<n<<endl;
for (int i = 0; i < n; i++){
Node* temp = que.front();
que.pop();
if (temp->left)
que.push(temp->left);
if (temp->right)
que.push(temp->right);
if (i == n-1)
temp->next = nullptr;
else
temp->next = que.front();
}
}
return root;
}
};
但是递归的方法很有意思
其实关于递归,这种递归属于前序遍历的递归,前序遍历以及后序遍历最大的区别就是,一个是自顶向下的处理问题,一个是自底向上的处理问题。
-
关于自顶向下处理问题,其实都是有套路的,我们要处理一个较大的问题,那么先解决当前节点的问题,然后将问题划分开来,将划分后的问题递归的解决,当然我们划分之后的子问题的问题规模一定是不断变小的。所以在整个递归函数的时候需要设置好递归的出口。这种问题有一个典型的特点就是数据之间的耦合联系非常少。关于自顶向下的处理问题,一定要有一定的记忆化思维,明白我们要解决什么样的问题,另外我们在往下递进的时候,我们要意识到我们已经解决了一部分问题,利用已经解决的部分递进解决还没有解决的问题。
-
关于自底向上的处理问题,我们需要开始时候不断的划分问题规模,将问题规模不断变小,然后减小到不能减小的时候,开始自底向下的不断解决问题,这里往往需要一个归并的操作,归并操作需要将每个小问题的解答连接起来。不断的连接,最后得到我们整个大问题的解答,一个典型的例子就是归并排序。
class Solution {
private:
void traversal(Node* cur) {
if (cur == NULL) return;
// 中
if (cur->left) cur->left->next = cur->right; // 操作1
if (cur->right) {
if (cur->next) cur->right->next = cur->next->left; // 操作2
else cur->right->next = NULL;
}
traversal(cur->left); // 左
traversal(cur->right); // 右
}
public:
Node* connect(Node* root) {
traversal(root);
return root;
}
};