(⊙_⊙) 基础做法:
* 枚举法:解决这类问题,通常我们的方法是枚举从 A 串的什么位置起开始与 B 匹配,然后验证是否匹配。
* 假如 A 串长度为 n,B 串长度为 m,那么这种方法的复杂度是O(mn) 的。
* 虽然很多时候复杂度达不到 O(mn)(验证时只看头一两个字母就发现不匹配了) ,但我们有许多“最坏情况”
- 比如,A= ”aaaaaaaaaaaaaaaaaaaaaaaaaab”,B=”aaaaaaaab”
引入KMP:
* 我们将介绍的是一种最坏情况下 O(n) 的算法(这里假设
m <= n) ,即传说中的 KMP 算法。
* KMP 算法的命名是因为这个算法是由 Knuth、Morris、Pratt三个提出来的,取了这三个人的名的头一个字母。
* 在网上能找到很多资料,最重要的理解则是“移动 (shift)” 、 “Next 函数” 、 “fail 指针”等概念。
* 在这里就通过一个具体的例子来理解 KMP 算法是如何实现的。
正式进入,dang dang dang~~
❶ KMP - KMP 算法 - i,j 指针
* 假如,A=”abababaababacb”,B=”ababacb”
* 我们用两个指针 i 和 j 分别表示,A[i − j + 1..i] 与 B[1..j] 完全相等
* 通过枚举,令 i 指针不断增加,而随着 i 的增加,j 也会相应地变化,且 j 仍然满足以 A[i] 结尾的长度为 j 的字符串正好匹配 B 串的前 j 个字符(j 当然越大越好) 。
* 指针 i 和 j 分别表示,A[i − j + 1..i] 与 B[1..j] 完全相等

* 注:当 i = 5 时,j 对应的为 5;当 j = 1,3 时也满足A[i − j + 1..i] = B[1..j] 的条件,但 j = 5 时是最大的
❷ KMP - KMP 算法 - 指针移动
* 接下来需要考虑,当 i 指针向后移动的时候,j 指针相应的变化
1. 当 A[i + 1] = B[j + 1] 时,顺利成章地,i 和 j 各加一;
2. 当 A[i + 1] != B[j + 1] 时,KMP 的策略是调整 j 的位置(减小 j值)使得 A[i − j ′ + 1..i] 与 B[1..j ′ ] 保持匹配,并且我们希望新的 B[j ′ + 1] 恰好与 A[i + 1] 匹配(从而使得 i 和 j ′ 能继续增加) 。

* 注:此时 i = j = 5,当 i 增加时,发现 A[6] ̸= B[6],故必须调整 j 的值
* 此时 j 不能等于 5 了,我们要把 j 改成比它小的值 j ′ ,同时满足A[i − j ′ + 1..i] 与 B[1..j ′ ]的性质。那么,j ′ 可能是多少呢?
* 我们发现,j ′ 必须要使得 B[1..j] 中的头 j ′ 个字母和末 j ′ 个字母完全相等

* 注:将 j = 5 调整到 j = 3,依然能够满足A[i − j + 1..i] = B[1..j];从图中可以看出 B[1..5] 中前三个必须与后三个相等,j = 3 才满足性质
❸ KMP - KMP 算法 - P 数组
* 从上面的这个例子,我们可以看到,新的 j 可以取多少与 i 无关,只与 B 串有关。
* 我们完全可以预处理出这样一个数组 P[j](也可以叫做 next,shift 数组) ,表示当匹配到 B 数组的第 j 个字母而第 j + 1个字母不能匹配了时,新的 j 最大是多少。
* P[j] 应该是所有满足 B[1..P[j]] = B[j − P[j] + 1..j] 的最大值。

* 注:对于图中的 B 串,满足 P[5] = 3
❹ KMP - KMP 算法 - 指针移动
* 当 A[i + 1] = B[j + 1] 时,顺利成章地,i 和 j 各加一;

* 注:这时候 A[6] = B[4] = b,所以我们往后推一位,得到i = 6,j = 4;再后来,A[7] = B[5],i 和 j 又各增加 1。
* 这时,又出现了 A[i + 1] ̸= B[j + 1] 的情况:

* 注:此时 i = 7,j = 5 且 A[8] ̸= B[6];由于 P[5] = 3, 因此新的j = 3
* 这时,新的 j = 3 仍然不能满足 A[i + 1] = B[j + 1],此时我们
再次减小 j 值,将 j 再次更新为 P[3]:

* 注:此时 i = 7,j = 3 且 A[8] ̸= B[4];由于 P[3] = 1, 因此新的j = 1
* 现在,i 还是 7,j 已经变成 1 了。而此时 A[8] 居然仍然不等于 B[j + 1]。这样,j 必须减小到 P[1],即 0:

* 注:此时 i = 7,j = 0,代表不存在 j 使得A[i − j + 1..i] = B[1..j]
❺ KMP - KMP 算法 - j = 0
* 终于,A[8] = B[1],i 变为 8,j 为 1。
* 事实上,有可能 j 到了 0 仍然不能满足 A[i + 1] = B[j + 1](比如 A[8] = ”d” 时) 。
* 因此,准确的说法是,当 j = 0 时,我们增加 i 值但忽略 j 直到出现 A[i] = B[1] 为止。

* 注:一直增加 i 直到出现 A[i] = B[1] 为止
❻ KMP - KMP 算法 - 代码实现
* 这个过程的代码很短(真的很短) ,我们在这里给出
int j=0;//j指针的初始值为0 for(int i=1; i<=n; i++) { //顺序枚举指针i,逐步增加 while(j>0&&A[i]!=B[j+1]) { j=P[j];//不匹配时减小j指针的值 } if(B[j+1] == A[i]) j=j+1; //匹配则i和j都增加1 if(j==m) {// 找到了一个匹配 cout<<"Pattern occurs with shift"<<i-m;// 这次匹配出现在 i-m 位置 j=P[j]; // 我们希望找到更多的匹配 } }
❼ KMP - KMP 时间复杂度分析
* 现在,我们还遗留了两个重要的问题:
1 为什么这个程序是线性的?(时间复杂度为 O(N))
2 如何快速预处理 P 数组。
* 为什么这个程序是 O(n) 的?其实,主要的争议在于,while 循环使得执行次数出现了不确定因素。
* 我们将用到时间复杂度的均摊分析中的主要策略:* 我们从上述程序的 j 值入手。每一次执行 while 循环都会使 j减小(但不能减成负的) ;使得j 值增加的地方只有第五行,而且每次 j 都只能加 1;因此,整个过程中 j 最多加了 n 个 1。于是,j 最多只有 n 次减小的机会。这告诉我们,while 循环总共最多执行了 n 次。
* 这样,整个过程显然是 O(n) 的。
❽ KMP - 预处理 P 数组
* 预处理不需要按照 P 的定义写成 O(m 2 ) 甚至 O(m 3 ) 的。
* 我们可以通过 P[1],P[2],…,P[j-1] 的值来获得 P[j] 的值* 对于刚才的B=”ababacb”,假如我们已经求出了 P[1], P[2],P[3] 和 P[4],看看我们应该怎么求出 P[5] 和 P[6]。
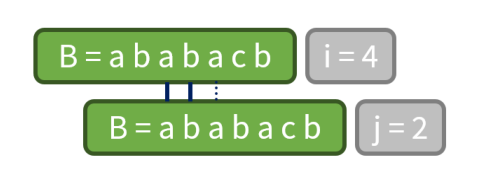
* P[5]=3 是因为 B[1..3] 和 B[3..5] 都是”aba”;而 P[3]=1则告诉我们,B[1],B[3] 和 B[5] 都是”a”。既然 P[6] 不能由P[5] 得到,或许可以由 P[3] 得到(如果 B[2] 恰好和 B[6]相等的话,P[6] 就等于 P[3]+1 了) 。
* 但 P[6] 也不能通过 P[3] 得到,因为 B[2]̸=B[6]。事实上,这样一直推到 P[1] 也不行,最后,我们得到,P[6]=0。

* 注:当 i=5,j=3 时,由于 B[6]̸=B[4],所以 j=P[3]=1;再由于 B[6]!=B[2],所以 j=P[1]=0
❾ KMP - 预处理 P 数组 - 代码实现
* 怎么这个预处理过程跟前面的 KMP 主程序这么像呢?其实,KMP的预处理本身就是一个 B 串“自我匹配”的过程(它的代码和上面的代码神似):
p[1]=0; j=0; for(int i=2; i<=m; i++) { while(j>0 && B[j+1] != B[i]) { // 减小 j 指针的值 j=P[j]; } if(B[j+1] == B[i]) { // 如果匹配则增加 j 指针的值 j+=1; } P[i] = j;// P 数组赋值 }
几个模板题,想练手的可以看一下:
http://www.cnblogs.com/wsdestdq/p/6821229.html
( ⊙ o ⊙ )! OK!!
只要还有明天,今天就是起跑线。相信自己,你并没有输在起跑线上!!