Codeforces 1092 F Tree with Maximum Cost (换根 + dfs)

题意：

给你一棵无根树，每个节点有个权值$a_i$，指定一个点u，定义$displaystyle value = sum^v a_i*dist(u,v)$，求value的最大值

n,ai<=2e5

思路：

其实就是找一个节点作为根满足上述最大的value

直接枚举是$O(n^2)$的，肯定不行，我们要用到换根法

换根适用于这种无根树找根，两个跟直接产生的结果又有联系，可以相互转换的情况

对于这一题，我们让sum[u] = 以u为根的子树的$sum a_i$

这样，从父亲节点u向儿子节点v转移的时候，

假设此时的value(整棵树以u为根)为res，我们要将res的值转化为以v为根的value

 

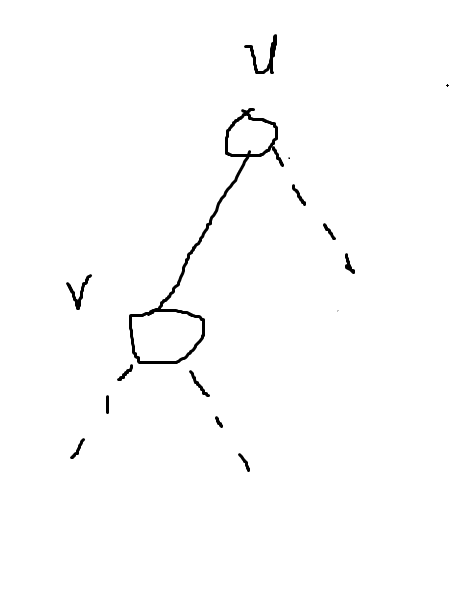
大前提：此时u是整棵树的根！         //没有这个大前提也可以，你要预处理一下每个节点祖先的$sum a_i$，然后在下面的操作中搞一下，但是我们完全可以通过只改变sum[u],sum[v]的值来决定到底谁才是整棵树的根，因为无论u，v谁是根，其他节点的sum[]都是不变的！嘻嘻

首先$value_v$相比$value_u$，根(v或u)与以v为根的子树中的每一个节点的距离都小了1

在value上表现为 res -= sum[v]

其次在以v为根的子树之外的节点，跟到那些节点的距离都大了1

所以sum[u] -= sum[v], res += sum[u]

此时因为v要成为整个树的根，所以sum[v]+=sum[u]

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<stack>
#include<queue>
#include<deque>
#include<set>
#include<vector>
#include<map>
#include<functional>
    
#define fst first
#define sc second
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define lson l,mid,root<<1
#define rson mid+1,r,root<<1|1
#define lc root<<1
#define rc root<<1|1
#define lowbit(x) ((x)&(-x)) 

using namespace std;

typedef double db;
typedef long double ldb;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PI;
typedef pair<ll,ll> PLL;

const db eps = 1e-6;
const int mod = 1e9+7;
const int maxn = 2e6+100;
const int maxm = 2e6+100;
const int inf = 0x3f3f3f3f;
const db pi = acos(-1.0);

vector<int>g[maxn];
int a[maxn];
ll res, ans;
ll sum[maxn];

void dfs(int x, int fa, int h){
    int sz = g[x].size();
    res += 1ll*h*a[x];
    sum[x] = a[x];
    for(int i = 0; i < sz; i++){
        if(g[x][i] == fa)continue;
        dfs(g[x][i], x, h+1);
        sum[x] += sum[g[x][i]];
    }
    return;
}

void dfs2(int x, int fa){
    ans = max(res, ans);
    int sz = g[x].size();
    for(int i = 0; i < sz; i++){
        int y = g[x][i];
        if(y == fa) continue;

        res -= sum[y];
        sum[x] -= sum[y];
        res += sum[x];
        sum[y] += sum[x];

        dfs2(y, x);

        sum[y] -= sum[x];
        res -= sum[x];
        sum[x] += sum[y];
        res += sum[y];
    }
    return;
}

int main(){
    int n;
    scanf("%d", &n);
    mem(sum, 0);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i]);
    }
    for(int i = 1; i < n; i++){
        int x, y;
        scanf("%d %d",&x,&y);
        g[x].pb(y);
        g[y].pb(x);
    }
    res = 0;
    ans = 0;
    dfs(1,-1,0);
    dfs2(1,-1);
    printf("%lld", ans);
    return 0;
}

/*

 */

 明天(今天)还得磨锤子，赶紧睡觉了