代码填空题
全排列 By 2018计蒜客蓝桥杯省赛B组模拟
相信大家都知道什么是全排列,但是今天的全排列比你想象中的难一点。我们要找的是全排列中,排列结果互不相同的个数。比如:aab 的全排列就只有三种,那就是aab,baa,aba。
代码框中的代码是一种实现,请分析并填写缺失的代码。

#include <cstdio> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int N=1e3; char str[N], buf[N];//buffer int vis[N], total, len; void arrange(int num) { if (num == len){ printf("%s ", buf); total++; return; } for (int i = 0; i < len; ++i) { if (!vis[i]) { int j; for (j = i + 1; j < len; ++j) { if (/*填入代码*/) { break; } } if (j == len) { vis[i] = 1; buf[num] = str[i]; arrange(num + 1); vis[i] = 0; } } } } int main() { while (~scanf("%s",str)) { len = strlen(str); sort(str, str + len); total = 0; buf[len] = '�'; arrange(0); printf("Total %d ", total); } return 0; }
这个函数可以求出去重后的全排列。如果不填入代码,输入aab,则输出aab aab aba aba baa baa。与题意不符,因此推断,填入代码所在的for循环是用来去重的。
第一个a作为第一个元素形成的序列有aab aba ,如果第二个a开头,那么形成的序列必然和先前的重复。
这种情况可以翻译成:str[j] == s[i] && vis[j] == 1 (存在 j > i),故填入代码str[i] == str[j] && vis[j]
快速幂 By 2018计蒜客蓝桥杯省赛B组模拟
一个数的整数次幂,是我们在计算中经常用到的,但是怎么可以在 O(log(n)) 的时间内算出结果呢?
代码框中的代码是一种实现,请分析并填写缺失的代码,求 x^ymod p 的结果。

#include <iostream> using namespace std; int pw(int x, int y, int p) { if (!y) { return 1; } int res = ——————————————; if (y & 1) { res = res * x % p; } return res; } int main() { int x, y, p; cin >> x >> y >> p; cout << pw(x, y, p) << endl; return 0; }
快速幂求余算法,链接,答案pw(x*x, y<<1, p)
Lis By 2018计蒜客蓝桥杯省赛B组模拟
LIS 是最长上升子序列。什么是最长上升子序列? 就是给你一个序列,请你在其中求出一段最长严格上升的部分,它不一定要连续。
就像这样:2, 3, 4, 7 和 2, 3, 4, 6 就是序列 2 5 3 4 1 7 6 的两个上升子序列,最长的长度是 4。

#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 9; int f[N], a[N]; int n; int find(int l, int r, int x) { while (l < r) { int mid = (l + r) / 2; if (f[mid] < x) { l = mid + 1; } else { r = mid; } } return l; } int lis() { int len = 0; for (int i = 0; i < n; i++) { ________ f[k] = a[i]; if (k == len) { len++; } } return len; } int main() { scanf("%d", &n); for (int i = 0; i < n; i++) { scanf("%d", a + i); } printf("%d ", lis()); return 0; }
O(logn)的LIS算法,答案 int k = find(0, len, a[i]);
信号匹配 By 蓝桥杯第五届B组决赛
从X星球接收了一个数字信号序列。
现有一个已知的样板序列。需要在信号序列中查找它首次出现的位置。这类似于串的匹配操作。
如果信号序列较长,样板序列中重复数字较多,就应当注意比较的策略了。可以仿照串的KMP算法,进行无回溯的匹配。这种匹配方法的关键是构造next数组。
next[i] 表示第i项比较失配时,样板序列向右滑动,需要重新比较的项的序号。如果为-1,表示母序列可以进入失配位置的下一个位置进行新的比较。
下面的代码实现了这个功能,请仔细阅读源码,推断划线位置缺失的代码。

// 生成next数组 int* make_next(int pa[], int pn) { int* next = (int*)malloc(sizeof(int)*pn); next[0] = -1; int j = 0; int k = -1; while(j < pn-1){ if(k==-1 || pa[j]==pa[k]){ j++; k++; next[j] = k; } else k = next[k]; } return next; } // da中搜索pa, da的长度为an, pa的长度为pn int find(int da[], int an, int pa[], int pn) { int rst = -1; int* next = make_next(pa, pn); int i=0; // da中的指针 int j=0; // pa中的指针 int n = 0; while(i<an){ n++; if(da[i]==pa[j] || j==-1){ i++; j++; } else __________________________; //填空位置 if(j==pn) { rst = i-pn; break; } } free(next); return rst; } int main() { int da[] = {1,2,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,2,1,2,1,1,2,1,1,2,1,1,1,2,1,2,3}; int pa[] = {1,2,1,1,2,1,1,1,2}; int n = find(da, sizeof(da)/sizeof(int), pa, sizeof(pa)/sizeof(int)); printf("%d ", n); return 0; }
KMP算法,答案 j = next[j];
打靶 By 蓝桥杯第七届A组决赛
小明参加X星球的打靶比赛。
比赛使用电子感应计分系统。其中有一局,小明得了96分。这局小明共打了6发子弹,没有脱靶。但望远镜看过去,只有3个弹孔。显然,有些子弹准确地穿过了前边的弹孔。
不同环数得分是这样设置的:
1,2,3,5,10,20,25,50
那么小明的6发子弹得分都是多少呢?有哪些可能情况呢?下面的程序解决了这个问题。

#include <stdio.h> #define N 8 void f(int ta[], int da[], int k, int ho, int bu, int sc) { int i,j; if(ho<0 || bu<0 || sc<0) return; if(k == N){ if(ho>0 || bu>0 || sc>0) return; for(i=0; i<N; i++){ for(j=0; j<da[i]; j++) printf("%d ", ta[i]); } printf(" "); return; } for(i=0; i<=bu; i++){ da[k] = i; f(ta, da, k+1,____, bu-i, sc-ta[k]*i); //填空位置 } da[k] = 0; } int main() { int ta[] = {1,2,3,5,10,20,25,50}; int da[N]; f(ta, da, 0, 3, 6, 96); return 0; }
先把函数的每个参数的含义搞清楚,第一个参数是不同环数的分数,第二个参数记录每一环中的环数,第三个参数k记录当前递归的层数(满为N),第四个参数是弹孔数量,第五个是射击次数,第六个是成绩。ok,此题就基本可以做出来了。
答案:ho - i==0? 0 : 1
棋子换位 By 蓝桥杯第七届B组决赛
有n个棋子A,n个棋子B,在棋盘上排成一行。它们中间隔着一个空位,用“.”表示,比如:AAA.BBB
现在需要所有的A棋子和B棋子交换位置。
移动棋子的规则是:
1. A棋子只能往右边移动,B棋子只能往左边移动。
2. 每个棋子可以移动到相邻的空位。
3. 每个棋子可以跳过相异的一个棋子落入空位(A跳过B或者B跳过A)。
AAA.BBB 可以走法:
移动A ==> AA.ABBB
移动B ==> AAAB.BB
跳走的例子:
AA.ABBB ==> AABA.BB

#include <stdio.h> #include <string.h> void move(char* data, int from, int to) { data[to] = data[from]; data[from] = '.'; } int valid(char* data, int k) { if(k<0 || k>=strlen(data)) return 0; return 1; } void f(char* data) { int i; int tag; int dd = 0; // 移动方向 while(1){ tag = 0; for(i=0; i<strlen(data); i++){ if(data[i]=='.') continue; if(data[i]=='A') dd = 1; if(data[i]=='B') dd = -1; if(valid(data, i+dd) && valid(data,i+dd+dd) && data[i+dd]!=data[i] && data[i+dd+dd]=='.'){ //如果能跳... move(data, i, i+dd+dd); printf("%s ", data); tag = 1; break; } } if(tag) continue; for(i=0; i<strlen(data); i++){ if(data[i]=='.') continue; if(data[i]=='A') dd = 1; if(data[i]=='B') dd = -1; if(valid(data, i+dd) && data[i+dd]=='.'){ // 如果能移动... if( ______________________ ) continue; //填空位置 move(data, i, i+dd); printf("%s ", data); tag = 1; break; } } if(tag==0) break; } } int main() { char data[] = "AAA.BBB"; f(data); return 0; }
如果把 if 那条语句注释掉,那么打印出的结果是
1移动 AA.ABBB
2跳走 AABA.BB
3移动 AAB.ABB
4跳走 A.BAABB
5移动 .ABAABB
6跳走 BA.AABB
7移动 B.AAABB
f函数中,第一个for循环是实现跳走的,第二个for循环是实现移动的,如果注释掉那条if语句,程序的“移动”功能是错误的。我们简单模拟程序运行的过程,第一个移动是不会错的,我们假设第二个移动错误,那么把AABA.BB这种情况抽象出来,那就是:
当data[i-dd] == data[i + dd +dd]的时候(i指向第三个A),不能移动
结合第一个for循环中,if条件语句的写法,我们还需要加上
valid(data, i –dd) && valid(data, i – dd –dd)
最终需要填入的代码为:data[i-dd] == data[i + dd +dd] && valid(data, i –dd) && valid(data, i – dd –dd) ,结果正确,假设成立。
代码填空,我们如果想主要通过模拟来推测代码,往往是比较困难的,因为我们模拟的想法和程序的作者的想法往往有差异,因此,可以通过注释其所在语句,来推测代码的功能,然后假设几种情况分别带入验证。
希尔伯特曲线 By 蓝桥杯第八届B组决赛
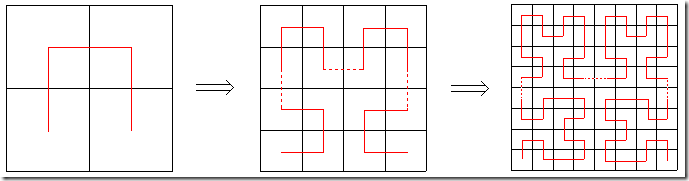
希尔伯特曲线是以下一系列分形曲线 Hn 的极限。我们可以把 Hn 看作一条覆盖 2^n × 2^n 方格矩阵的曲线,曲线上一共有 2^n *2^n 个顶点(包括左下角起点和右下角终点),恰好覆盖每个方格一次。 Hn(n > 1)可以通过如下方法构造:
1. 将 Hn-1 顺时针旋转90度放在左下角
2. 将 Hn-1 逆时针旋转90度放在右下角
3. 将2个 Hn-1 分别放在左上角和右上角
4. 用3条单位线段把4部分连接起来
对于 Hn 上每一个顶点 p ,
我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标(左下角是(1, 1),右上角是(2^n, 2^n),从左到右是X轴正方向,从下到上是Y轴正方向), 定义 p 的序号是它在曲线上从起点开始数第几个顶点(从1开始计数)。 以下程序对于给定的n(n <= 30)和p点坐标(x, y),输出p点的序号。

#include <stdio.h> long long f(int n, int x, int y) { if (n == 0) return 1; int m = 1 << (n - 1); if (x <= m && y <= m) { return f(n - 1, y, x); } if (x > m && y <= m) { return 3LL * m * m + f(n - 1,__, 2 * m - x + 1); //填空 } if (x <= m && y > m) { return 1LL * m * m + f(n - 1, x, y - m); } if (x > m && y > m) { return 2LL * m * m + f(n - 1, x - m, y - m); } } int main() { int n, x, y; scanf("%d %d %d", &n, &x, &y); printf("%lld", f(n, x, y)); return 0; }
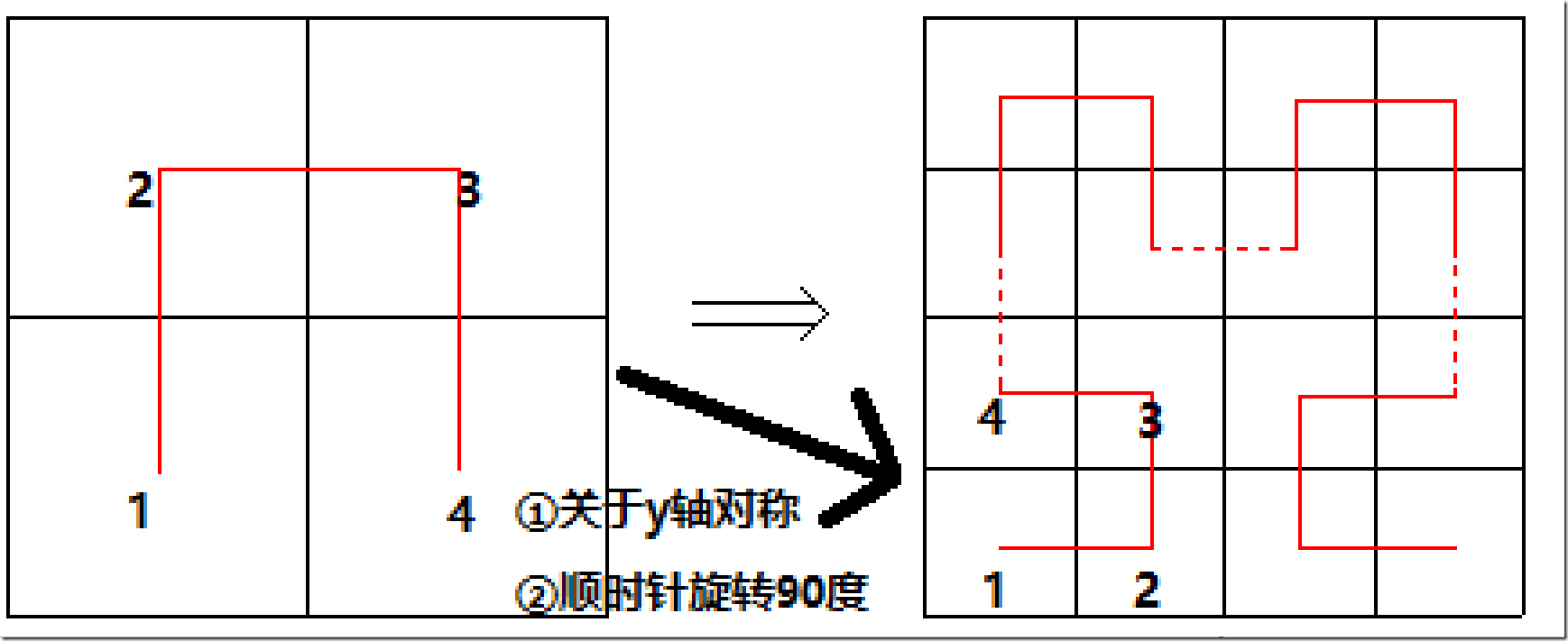
先读懂题意,就拿第一个图和第二个图来讲,第一个图经过了①关于x轴的对称变换(-x, y) 在经过②顺时针旋转90度变换(y,x)
因此第一个if语句中填入的是f(n-1,y,x),n-1是递归降阶,懂了第一个,剩下的三个if语句也就很好理解了。答案:m-y-1
瓷砖样式 By 蓝桥杯第八届B组决赛
小明家的一面装饰墙原来是 3*10 的小方格。 现在手头有一批刚好能盖住2个小方格的长方形瓷砖。
瓷砖只有两种颜色:黄色和橙色。
小明想知道,对于这么简陋的原料,可以贴出多少种不同的花样来。 小明有个小小的强迫症:忍受不了任何2*2的小格子是同一种颜色。
(瓷砖不能切割,不能重叠,也不能只铺一部分。另外,只考虑组合图案,请忽略瓷砖的拼缝)
显然,对于 2*3 个小格子来说,口算都可以知道:一共10种贴法,如图所示
但对于 3*10 的格子呢?肯定是个不小的数目,请你利用计算机的威力算出该数字。
利用位来去重,一共30个瓷砖,也就是30位,int是32位,因此int足够用。

#include <stdio.h> #include <string.h> #include <map> #include <algorithm> #include <iostream> using namespace std; const int w = 3, h = 10; int graph[w][h]; int ans = 0; map<int, int> Hash; //检查2x2格子中颜色是否相同 bool check_color() { for (int i = 0; i < w; i++) { for (int j = 0; j < h; j++) { if (i + 1 < w && j + 1 < h) if ((graph[i][j] + graph[i][j + 1] + graph[i + 1][j] + graph[i + 1][j + 1]) % 4 == 0) return false; } } return true; } //检测方案是否有重复 bool check_repeat() { int ret = 0, bit = 1; for (int i = 0; i < w; i++) { for (int j = 0; j < h; j++) { ret += graph[i][j] * bit; bit <<= 1; } } //此涂色方案未曾出现 if (Hash.count(ret) == 0) { Hash[ret] = 1; return true; } else return false; } void fill_with_tile(int n) { //已经铺满 if (n == w * h) { if (check_color() == true && check_repeat() == true) ans++; return; } int x = n / h; int y = n % h; //此块未被涂色 if (graph[x][y] == -1) { //横向摆放 if (y + 1 < h && graph[x][y + 1] == -1) { //枚举两种颜色 for (int i = 0; i < 2; i++) { graph[x][y] = graph[x][y + 1] = i; fill_with_tile(n + 1); //回溯 graph[x][y] = graph[x][y + 1] = -1; } } //纵向摆放 if (x + 1 < w && graph[x + 1][y] == -1) { //枚举两种颜色 for (int i = 0; i < 2; i++) { graph[x][y] = graph[x + 1][y] = i; fill_with_tile(n + 1); //回溯 graph[x][y] = graph[x + 1][y] = -1; } } } else fill_with_tile(n + 1); } int main() { memset(graph, -1, sizeof(graph)); fill_with_tile(0); printf("%d ", ans); return 0; }