【CF1257F】Make Them Similar【meet in the middle+hash】

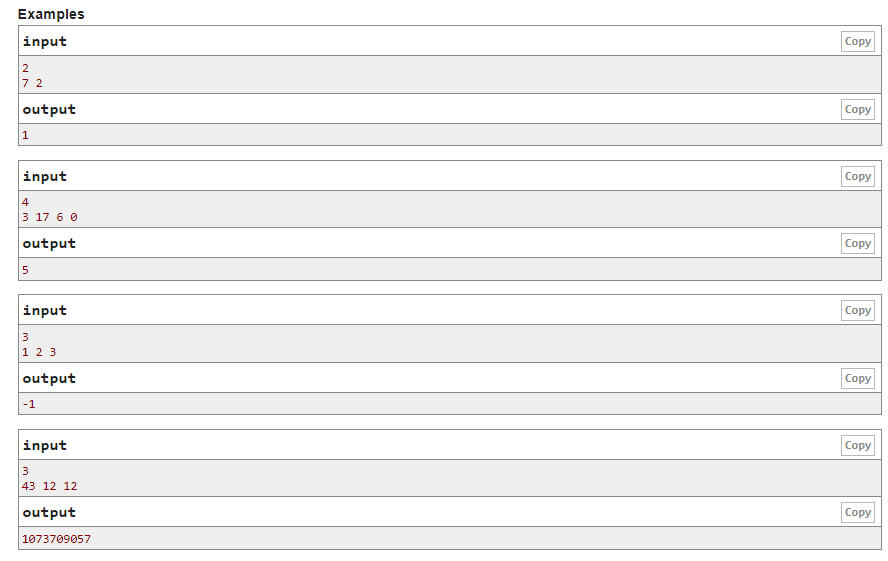
题意：给定n个数，让你给出一个数，使得n个数与给出的数异或后得到的数的二进制表示中1的数量相同

题解：考虑暴搜2^30去找答案，显然不可接受

显然可以发现，这是一个经典的meet in the middle模型，直接套用然后hash一下即可

设前15位异或完之后1的个数为ai，那么差分一下得

a1  a2-a1  a3-a2  a4-a3  ......

设后15位异或之后1的个数为bi，那么查分一下得

b1  b2-b1  b3-b2  b4-b3  ......

差分完之后表示的是后一个数1的个数与前一个数的区别，当所有的ai-ai-1+bi-bi-1都为0时，则表示后一个数和前一个数的1的个数相同

即a2-a1=-(b2-b1)

所以只要将后15位得到的bi数组取相反数即可

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<map>
#define ll long long
#define mod 145141247483647
using namespace std;
int bit[33000],a[101],b[101];
int n;
map<ll,int> fl;
map<ll,int>::iterator I;
const int T=(1<<15)-1;
int main()
{
    for(int i=1;i<=32768;i++)bit[i]=bit[i>>1]+(i&1);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=0;i<=32767;i++)
    {
      for(int j=1;j<=n;j++)b[j]=(a[j]>>15)^i;
      for(int j=n;j>1;j--)b[j]=bit[b[j]]-bit[b[j-1]]+666;
      ll t=0;
      for(int j=2;j<=n;j++)t=(t*53+b[j]+mod)%mod;
      fl[t]=i;
    }
    for(int i=0;i<=32767;i++)
    {
      for(int j=1;j<=n;j++)b[j]=(a[j]&T)^i;
      for(int j=n;j>1;j--)b[j]=-bit[b[j]]+bit[b[j-1]]+666;
      ll t=0;
      for(int j=2;j<=n;j++)t=(t*53+b[j]+mod)%mod;
      I=fl.find(t);
      if(I!=fl.end())
      {
        return !printf("%d
",((*I).second<<15)+i);
      }
    }
    return !printf("-1");
}