题目:将一个n元一维数组a[n]左移i个位置。例如,当n=8,i=3时,数组abcdefgh旋转为defghabc。请设计一个算法完成这个任务。
1. 块交换法:
分析:将n元一维数组a[n]分解为两块,将第一块存储在临时数组中,将第二块前移i个单位,再将临时数组加入到第二块后面。
如:n=8,i=3时,将第一块abc存储为临时变量,第二块defgh前移3个单位,再将abc放入到defgh后面。
思考:这种方法最大的缺陷至少需要与两块中较小的一块大小的临时变量。
2.杂技算法
分析:将a[0]存储在一个临时变量中,然后将a[i]替换a[0],a[2i]替换a[i]….当一个循环结束的时候,若替换次数小于n,则从a[1]开始替换…,需要经过gcd(n,i)(n和i的最大公约数)次循环后,才能把每一个元素都移到该移的地方。
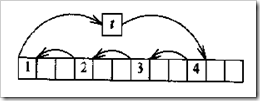
下面是代码实现:
#include<iostream> using namespace std; //求最大公约数 //辗转相除法 int gcd(int a, int b) { while( a!= 0) { if(a>=b) a-=b; else { int t=a; a=b; b=t; } } return b; } //杂技算法 void Rotate1(char* a,int lenth,int rotateLen) { int gcdNum = gcd(lenth,rotateLen); for(int i=0; i<gcdNum; i++) { int temp = a[i]; int first = i; while(1) { int second = (first+rotateLen)% lenth; if(second == i) break; a[first] = a[second]; first = second; } a[first] = temp; } } int main() { char a[9] = "abcdefgh"; Rotate1(a,8,3); }
3. 求逆算法
分析:将a[n]看做是向量BC组成,最终的结果需要时CB,过程如下:将BC各分别取逆B^-1C^-1,再对整个式子取逆,得到CB。
举例:将abcdefgh中的abc看做向量B,defgh看做向量C。
下面是代码实现:
代码 #include<iostream> using namespace std; void Revert(char* str,int start,int end) { while(start<end) { char temp = str[start]; str[start] = str[end]; str[end] = temp; start++; end--; } } void Rotate1(char* a,int start,int end) { Revert(a,0,2); Revert(a,3,7); Revert(a,0,7); } int main() { char a[9] = "abcdefgh"; Rotate1(a,0,7); }