FFT模板 生成函数 原根 多项式求逆 多项式开根

FFT

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 1000005
using namespace std;
inline int read() {
    int x=0,f=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
double pi=acos(-1.0);
struct complex {
    double x,y;
    complex (double xx=0,double yy=0) {x=xx;y=yy;}
    complex operator +(const complex b) const {return complex(x+b.x,y+b.y);}
    complex operator -(const complex b) const {return complex(x-b.x,y-b.y);}
    complex operator *(const complex b) const {return complex(x*b.x-y*b.y,x*b.y+y*b.x);}
}a[maxn],b[maxn];
int n,m;
int limit=1,l,pos[maxn];
void FFT(complex *A,int tp) {
    for(int i=0;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
    for(int mid=1;mid<limit;mid<<=1) {
        complex wn(cos(pi/mid),tp*sin(pi/mid));
        for(int R=mid<<1,j=0;j<limit;j+=R) {
            complex w(1,0);
            for(int k=0;k<mid;k++,w=w*wn) {
                complex x=A[j+k],y=w*A[j+mid+k];
                A[j+k]=x+y;
                A[j+mid+k]=x-y;
            }
        }
    }
    return ;
}
int main() {
    n=read(),m=read();
    for(int i=0;i<=n;i++) a[i].x=read();
    for(int i=0;i<=m;i++) b[i].x=read();
    while(limit<=n+m) limit<<=1,l++;
    for(int i=0;i<limit;i++) pos[i]=(pos[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a,1);
    FFT(b,1);
    for(int i=0;i<limit;i++) a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/limit+0.5));
}

 生成函数

小A有ai个价值为Ai的物品，小B有bi个价值为Ai的物品，求用两个组成价值为ci的方案数

生成函数可以解决上面的这个问题，构造两个多项式，第X的Ai次方项的系数表示价值为i的物品有多少个，对两个人分别构造，乘在一起的多项式就代表所有的方案数。

原根

定义P的原根为满足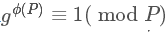的整数g。 

NTT

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 4000001
#define mod 998244353
#define ll long long 
using namespace std;
inline int read() {
    int x=0,f=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
ll a[maxn],b[maxn],pos[maxn];
ll n,m,limit=1,l,g=3;
ll power(ll x,ll y) {
    ll ans=1;
    while(y) {
        if(y&1) ans*=x,ans%=mod;
        x*=x,x%=mod;y>>=1;
    }
    return ans;
}
void NTT(ll *A,int tp) {
    for(int i=0;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
    for(int mid=1;mid<limit;mid<<=1) {
        ll wn=power(g,(mod-1)/(mid<<1));
        if(tp==-1) wn=power(wn,mod-2);
        for(int j=0;j<limit;j+=(mid<<1)) {
            ll w=1;
            for(int k=0;k<mid;k++,w*=wn,w%=mod) {
                ll x=A[j+k],y=w*A[j+mid+k];
                A[j+k]=x+y;A[j+k]=(A[j+k]%mod+mod)%mod;
                A[j+mid+k]=x-y;A[j+mid+k]=(A[j+mid+k]%mod+mod)%mod;
            }
        }
    }
    if(tp==-1) {
        ll ny=power(limit,mod-2);
        for(int i=0;i<limit;i++) A[i]*=ny,A[i]=(A[i]%mod+mod)%mod;
    }
}
int main() {
    n=read(),m=read();
    for(int i=0;i<=n;i++) a[i]=read();
    for(int i=0;i<=m;i++) b[i]=read();
    while(limit<=n+m) limit<<=1,l++;
    for(int i=0;i<limit;i++) pos[i]=(pos[i>>1]>>1)|((i&1)<<(l-1));
    NTT(a,1);
    NTT(b,1);
    for(int i=0;i<limit;i++) a[i]=a[i]*b[i],a[i]=(a[i]%mod+mod)%mod;
    NTT(a,-1);
    for(int i=0;i<=n+m;i++) printf("%lld ",a[i]);
}

多项式求逆

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
#define mod 998244353
#define maxn 1000000
using namespace std;
inline int read() {
    int x=0,f=1;char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
ll g=3,limit=1,l,n;
ll a[maxn],b[maxn],pos[maxn],c[maxn];
ll power(ll x,ll y) {
    ll ans=1;
    while(y) {
        if(y&1) ans*=x,ans%=mod;
        x*=x,x%=mod;y>>=1;
    }
    return ans;
}
void NTT(ll *A,int tp) {
    for(int i=0;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
    for(int mid=1;mid<limit;mid<<=1) {
        ll wn=power(g,(mod-1)/(mid<<1));
        if(tp==-1) wn=power(wn,mod-2);
        for(int j=0;j<limit;j+=(mid<<1)) {
            ll w=1;
            for(int k=0;k<mid;k++,w*=wn,w%=mod) {
                ll x=A[j+k],y=w*A[j+mid+k]%mod;
                A[j+k]=x+y;A[j+k]=(A[j+k]%mod+mod)%mod;
                A[j+mid+k]=x-y;A[j+mid+k]=(A[j+mid+k]%mod+mod)%mod;
            }
        }
    }
    if(tp==-1) {
        ll ny=power(limit,mod-2);
        for(int i=0;i<limit;i++) A[i]*=ny,A[i]=(A[i]%mod+mod)%mod;
    }
}
int d[maxn];
void inv(int step,ll *A,ll *B) {
    if(step==1) {B[0]=power(A[0],mod-2);return;}
    inv((step+1)>>1,A,B);
    l=0,limit=1;
    while(limit<=(step<<1)) limit<<=1,l++;
    for(int i=0;i<limit;i++) pos[i]=(pos[i>>1]>>1)|((i&1)<<(l-1));
    for(int i=0;i<step;i++) c[i]=A[i];
    for(int i=step;i<limit;i++) c[i]=0;
    NTT(c,1);NTT(B,1);
    for(int i=0;i<limit;i++) B[i]=((2ll-c[i]*B[i]%mod)+mod)%mod*B[i]%mod;
    NTT(B,-1);
    for(int i=step;i<limit;i++) B[i]=0;
}
int main() {
    n=read();
    for(int i=0;i<n;i++) a[i]=read();
    inv(n,a,b);
    for(int i=0;i<n;i++) printf("%lld ",b[i]);
}

多项式开根

void getsqr(ll *A,ll *B,ll len) {
    if(len==1) {B[0]=1;return;}
    getsqr(A,B,(len+1)>>1);
    memset(invb,0,sizeof(invb));
    getinv(B,invb,len);
    l=0,limit=1;
    while(limit<=(len<<1)) limit<<=1,l++;
    for(int i=0;i<limit;i++) pos[i]=(pos[i>>1]>>1)|((i&1)<<(l-1));
    for(int i=0;i<len;i++) c[i]=A[i];
    for(int i=len;i<limit;i++) c[i]=0;
    NTT(invb,1);NTT(c,1);NTT(B,1);
    for(int i=0;i<limit;i++) {B[i]=((c[i]*invb[i]%mod)*inv2%mod+B[i]*inv2)%mod;}
    NTT(B,-1);
    for(int i=len;i<limit;i++) B[i]=0;
}