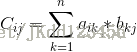一、
先介绍以下矩阵的基础知识
矩阵:有 n 行 m 列组成一个 n*m 的矩阵
a.结合性 (AB)C=A(BC).
b.对加法的分配性 (A+B)C=AC+BC,C(A+B)=CA+CB .
c.对数乘的结合性 k(AB)=(kA)B =A(kB).
d.关于转置 (AB)'=B'A'.
1.
矩阵的加减运算
满足的条件:两个矩阵的行、列 必须相同
2.
矩阵的乘运算
满足的条件:
A矩阵的列数为 B矩阵的行数
A(ms)*B(sn)=C(mn)
得到的矩阵 C 是 m 行 n 列的
其中 c[i][j] 为A 的第 i 行与B的第j 列对应乘积的和
即:
代码:
1 const int N=100; 2 int c[N][N]; 3 void multi(int a[m][s],int b[s][n])//n是矩阵大小,n<N 4 { 5 memset(c,0,sizeof c); 6 for(int i=1;i<=m;i++){ 7 for(int j=1;j<=n;j++){ 8 for(int k=1;k<=s;k++){ 9 c[i][j]+=a[i][k]*b[k][j]; 10 c[i][j]%=mod;//一定要在求和之后在 mod 11 } 12 } 13 } 14 }
二、
单位矩阵:
在矩阵的乘法中,有一种矩阵起着特殊的作用,如同数的乘法中的1,这种矩阵被称为单位矩阵。它是个方阵,从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
简记: I 或 E
性质:
1、根据矩阵乘法的定义,单位矩阵的重要性质为:
AE=EA=A
2、单位矩阵的特征值皆为1,任何向量都是单位矩阵的特征向量。
3、因为特征值之积等于行列式,所以单位矩阵的行列式为1。因为特征值之和 等于迹数,单位矩阵的迹为 n

三、
快速幂的思想:
假设我们要求a^b,最朴素的方法就是不断地乘a,乘b次,复杂度O(b)。
如果b很大,10^9,就需要用快速幂的思想。
例:a=3,b=100;
100的二进制为:1100100
也就是100可以化成64+32+4。
所以原数可以化成a^64*a^32*a^4
算法流程:
判断1100100的每一位是否为1,如果是1,就乘对应的二进制次幂。以此类推,直到乘完全部的位数。
时间复杂度O(log n)
1 /*一般快速幂的模板*/ 2 int quickpow(int a,int b){ 3 ans=1; 4 while(b){ 5 if(b&1) ans*=a; 6 a*=a; 7 b>>=1; 8 } 9 return ans; 10 }
(快速幂详解
https://www.cnblogs.com/wkfvawl/p/9125224.html)
四、
矩阵与DP
a[i]=a[i-1]+b[i-1]+1,b[i]=2*a[i-1]-5 ;a[1]=1,b[1]=1,问a[x]=?,b[x]=?
很简单的递推,一步步推即可,但是,如果x是10^9,如何推?
思维:递推式可以化为矩阵乘积
那么,矩阵A[i]=A[i-1]*B;
A[i+1]=A[i]*B=A[i-1]*B*B
A[x]=A[1]*B*B*B.......=A[1]*( B^(x-1) );
因为矩阵乘积可以换乘积顺序,所以可以先算出B^(x-1),如何计算呢?
快速幂!
问题迎刃而解~
1.构造出递推矩阵
2.对构造出的矩阵B,进行B^x的快速幂,乘积换成矩阵乘法。
3.最后矩阵的第一行第一列和第二列就是a[x]和a[y]。
其实快速幂和矩阵快速幂是异曲同工,但是往往构造矩阵是难点,转载一个别人博客写的矩阵构造方法:
Fibonacci数列:F(0)=1 , F(1)=1 , F(n)=F(n-1)+F(n-2)
我们以前快速求Fibonacci数列第n项的方法是 构造常系数矩阵
(一) Fibonacci数列f[n]=f[n-1]+f[n-2],f[1]=f[2]=1的第n项快速求法(不考虑高精度)
解法:
考虑1×2的矩阵【f[n-2],f[n-1]】。根据Fibonacci数列的递推关系,我们可以通过乘以一个2×2的矩阵A,得到矩阵:【f[n-1],f[n]】。
即:【f[n-2],f[n-1]】*A = 【f[n-1],f[n]】=【f[n-1],f[n-1]+f[n-2]】
很容易构造出这个2×2矩阵A,即:
0 1
1 1
所以,有【f[1],f[2]】×A=【f[2],f[3]】
又因为矩阵乘法满足结合律,故有:
【f[1],f[2]】×A ^(n-1) =【f[n],f[n+1]】
这个矩阵的第一个元素f[n]即为所求。


(二) 数列f[n]=f[n-1]+f[n-2]+1,f[1]=f[2]=1的第n项的快速求法(不考虑高精度)
解法:
仿照前例,考虑1×3的矩阵【f[n-2],f[n-1],1】,希望求得某3×3的矩阵A,使得此1×3的矩阵乘以A得到矩阵:【f[n-1],f[n],1】
即:【f[n-2],f[n-1],1】* A =【f[n-1],f[n],1】=【f[n-1],f[n-1]+f[n-2]+1,1】
容易构造出这个3×3的矩阵A,即:
0 1 0
1 1 0
0 1 1
故:【f[1],f[2],1】* A^(n-1) = 【f[n],f[n+1],1】
(三)数列f[n]=f[n-1]+f[n-2]+n+1,f[1]=f[2]=1的第n项的快速求法(不考虑高精度).
解法:
仿照前例,考虑1×4的矩阵【f[n-2],f[n-1],n,1】,希望求得某4×4的矩阵A,使得此1×4的矩阵乘以A得到矩阵:【f[n-1],f[n],n+1,1】
即:【f[n-2],f[n-1],n,1】* A = 【f[n-1],f[n],n+1,1】=【f[n-1],f[n-1]+f[n-2]+n+1,n+1,1】
容易构造出这个4×4的矩阵A,即:
0 1 0 0
1 1 0 0
0 1 1 0
0 1 1 1
故:【f[1],f[2],3,1】* A^(n-1) = 【f[n],f[n+1],n+2,1】
(四) 数列f[n]=f[n-1]+f[n-2],f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).
解法:
仿照之前的思路,考虑1×3的矩阵【f[n-2],f[n-1],s[n-2]】,我们希望通过乘以一个3×3的矩阵A,得到1×3的矩阵:【f[n-1],f[n],s[n-1]】
即:【f[n-2],f[n-1],s[n-2]】 * A = 【f[n-1],f[n],s[n-1]】=【f[n-1],f[n-1]+f[n-2],s[n-2]+f[n-1]】
容易得到这个3×3的矩阵A是:
0 1 0
1 1 1
0 0 1
这种方法的矩阵规模是(r+1)*(r+1)
f(1)=f(2)=s(1)=1 ,所以,有
【f(1),f(2),s(1)】* A = 【f(2),f(3),s(2)】
故:【f(1),f(2),s(1)】* A^(n-1) = 【f(n),f(n+1),s(n)】
(五) 数列f[n]=f[n-1]+f[n-2]+n+1,f[1]=f[2]=1的前n项和s[n]=f[1]+f[2]+……+f[n]的快速求法(不考虑高精度).
解法:
考虑1×5的矩阵【f[n-2],f[n-1],s[n-2],n,1】,
我们需要找到一个5×5的矩阵A,使得它乘以A得到如下1×5的矩阵【f[n-1],f[n],s[n-1],n+1,1】
即:【f[n-2],f[n-1],s[n-2],n,1】* A =【f[n-1],f[n],s[n-1],n+1,1】
=【f[n-1], f[n-1]+f[n-2]+n+1,s[n-2]+f[n-1],n+1,1】
容易构造出A为:
0 1 0 0 0
1 1 1 0 0
0 0 1 0 0
0 1 0 1 0
0 1 0 1 1
故:【f(1),f(2),s(1),3,1】* A^(n-1) = 【f(n),f(n+1),s(n),n+2,1】
一般地,如果有f[n]=p*f[n-1]+q*f[n-2]+r*n+s
可以构造矩阵A为:
0 q 0 0 0
1 p 1 0 0
0 0 1 0 0
0 r 0 1 0
0 s 0 1 1
更一般的,对于f[n]=Sigma(a[n-i]*f[n-i])+Poly(n),其中0<i<=某常数c, Poly (n)表示n的多项式,我们依然可以构造类似的矩阵A来解决问题。
设Degree(Poly(n))=d, 并规定Poly(n)=0时,d=-1,此时对应于常系数线性齐次递推关系。则本方法求前n项和的复杂度为:
((c+1)+(d+1))3*logns
例如:A(0) = 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2);给定三个值N,X,Y求S(N):S(N) = A(0)2 +A(1)2+……+A(n)2。
解:
考虑1*4 的矩阵【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】
我们需要找到一个4×4的矩阵A,使得它乘以A得到1×4的矩阵
【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
即:【s[n-2],a[n-1]^2,a[n-2]^2,a[n-1]*a[n-2]】* A = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
= 【s[n-2]+a[n-1]^2 , x^2 * a[n-1]^2 + y^2 * a[n-2]^2 + 2*x*y*a[n-1]*a[n-2] ,
a[n-1]^2 , x*a[n-1]^2 + y*a[n-2]a[n-1]】
可以构造矩阵A为:
1 0 0 0
1 x^2 1 x
0 y^2 0 0
0 2xy 0 y
故:【S[0],a[1]^2,a[0]^2,a[1]*a[0]】 * A^(n-1) = 【s[n-1],a[n]^2,a[n-1]^2,a[n]*a[n-1]】
所以:【S[0],a[1]^2,a[0]^2,a[1]*a[0]】 * A^(n) = 【s[n],a[n+1]^2,a[n]^2,a[n+1]*a[n]】
若A = (B * C ) 则AT = ( B * C )T = CT * BT
故