NFA到DFA的转换

一、有限自动机

1、不确定的有限自动机（NFA）

• 只要有一条路径能够使一个字符串从初始态到达接收态就称这个字符串是接收的
• 匹配结果，是不确定的
• 慢，有Backtrack（回溯）
• 基于表达式
• 某时刻可能处于一组状态之中的任何一个，因此记录所有的可能路径

2、确定的有限自动机（DFA）

• 匹配速度，是确定的
• 快，无Backtrack（回溯）
• 基于文本
• 在任意时刻必定处于某个确定状态

二、NFA到DFA转换

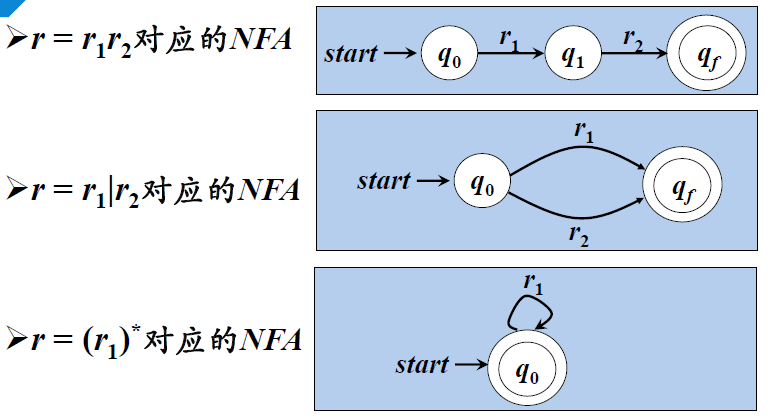
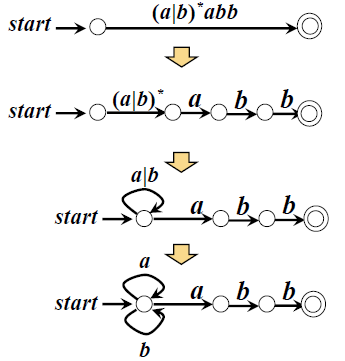
1、根据RE构造NFA

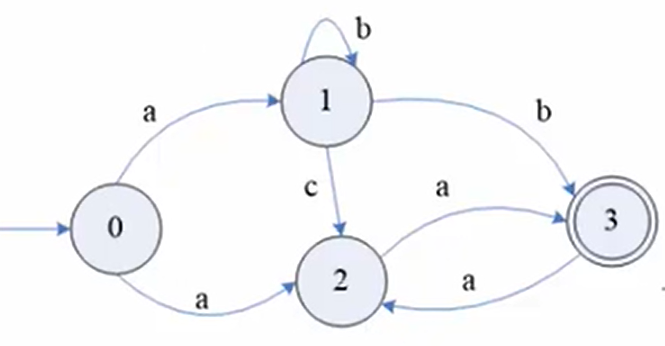
2、NFA转为DFA

又称NFA的确定化

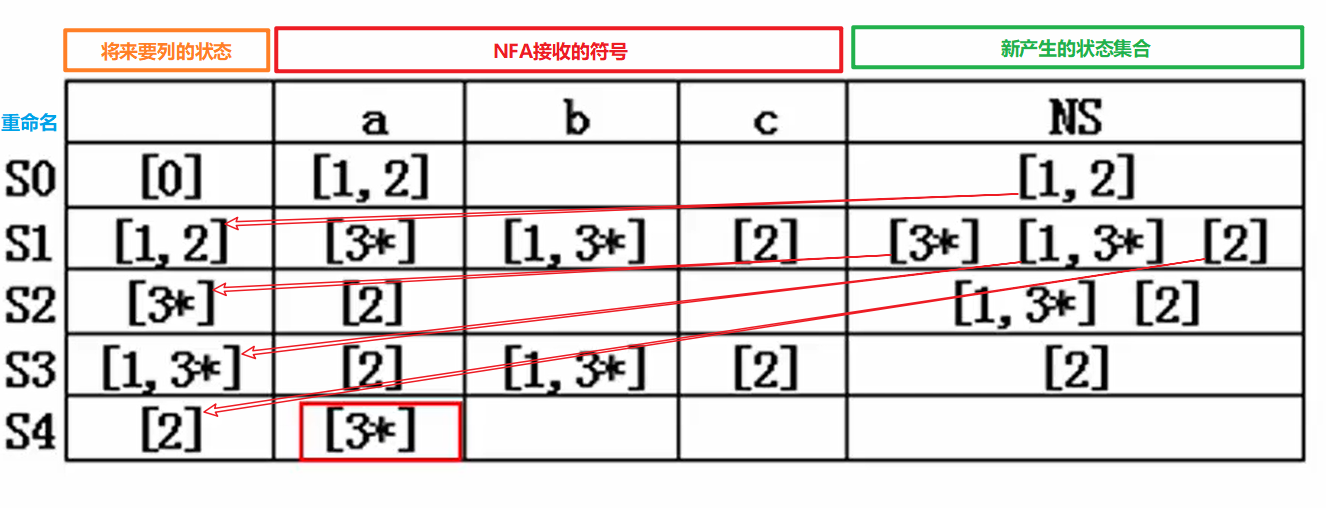
状态转换表

注：标有*为接收状态 带ε

边记得增加一列

1. NFA的开始状态集合为[0]，将NFA将接收的符号代入当前状态，最长子串原则，得出新产生的状态
2. 将新产生的状态作为将来要列出的状态重复1中步骤
3. 直至新产生的状态集合中无新集合时结束
4. 将第一列中将来要列的状态重命名

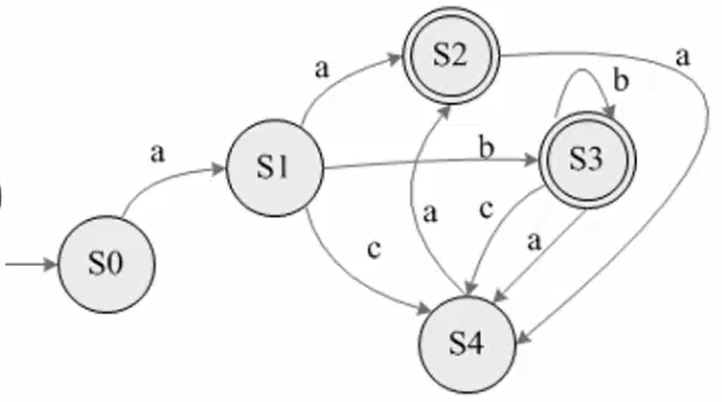
转换为DFA

1. S₀为初始状态，根据状态转换表中NFA接受的符号产生的集合到重命名中寻找匹配的状态
2. 画图，根据新的圈重复1中步骤，直至结束
3. 重命名中标有*的接受态要用双圈标出

计算ε-closure(T)：