什么是“矩”?
网上都说矩的概念在《概率论与数理统计》那本书上,可是我考研没考到,我又看了一遍还是没找到。。。
先说一下矩在数学中的定义:
在数学的概率领域中有一类数字特征叫矩.(X^k为X的k次方)
k阶矩定义:设X为随机变量,c为常数,k为正整数,如果E[|X-c|^c]<无穷大,则称E[(X-c)^k]为X关于点c的k阶矩.
原点矩:对于正整数k,如果E|X^k|<无穷,称Vk=E(X^k) 为随机变量X的k阶原点矩.X的数学期望是X的一阶原点矩,即E(x)=v1.
c=0时,称其为X的k阶原点矩。
其中k=1时,E(X)就是期望=平均值。
c=E[X](均值)时,称为k阶中心矩。
其中k=2时,E{[X-E(X)]^2}就是方差.
E()=均值。
在知乎的论坛上看到一些人的评论很好:https://www.zhihu.com/question/23236070



矩在图像中的应用
图像是一个二维的数据,那么就可以用二维函数去表示--->>>f(x,y)=Mat image; 那么图像变成函数之后就可以用矩的概念去表示了。
公式就不说了,网站和书籍上很多都是!
从公式可以看出:几何矩是可以改变的,比如图像偏移之后数据改变,那么中心矩就改变了。
中心矩是基本不变的,因为其中有了质心的加入。
中心矩和几何矩推导出的几个不变矩公式,是不变的,这个具体怎么不变的,我也没找到资料,从中心矩就是基本不变的,再进行数学计算推导不变矩是可以的。
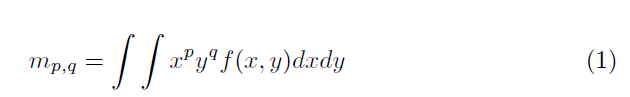 可以看出来,m(0,0)就是面积的意思
可以看出来,m(0,0)就是面积的意思


参考:知乎
http://www.cnblogs.com/ronny/p/3985810.html