普通莫队
SP3267 DQUERY - D-query
(mathcal{Description})
给出一个长度为 (n) 的数列,有 (q) 个询问,需要求出在 ((l, r)) 区间内有多少不同的数
(mathcal{Solution})
这题就是 [SDOI2009]HH的项链 的数据弱化版,可以把他当做莫队的模板题。
考虑最简单的做法,也就是暴力,用一个 (cnt) 数组记录 ([l, r]) 区间内(暴力扫一遍)每个数出现的次数,再扫一遍 (cnt) 数组统计不为 (0) 的个数,输出答案。
很容易想出第一步优化,在记录 (cnt) 数组的同时,在加之前判断下是否为 (0),也就是之前有没有出现过这个数,如果为 (0) 那么(ans++)。
再考虑下优化,我们可以弄两个指针 (l) 、(r) ,每次询问移动 (l)、(r) 到询问的区间,统计 (ans) 时只需在两个指针处加减 (cnt)。
当然如果他需要查找的区间是这样的
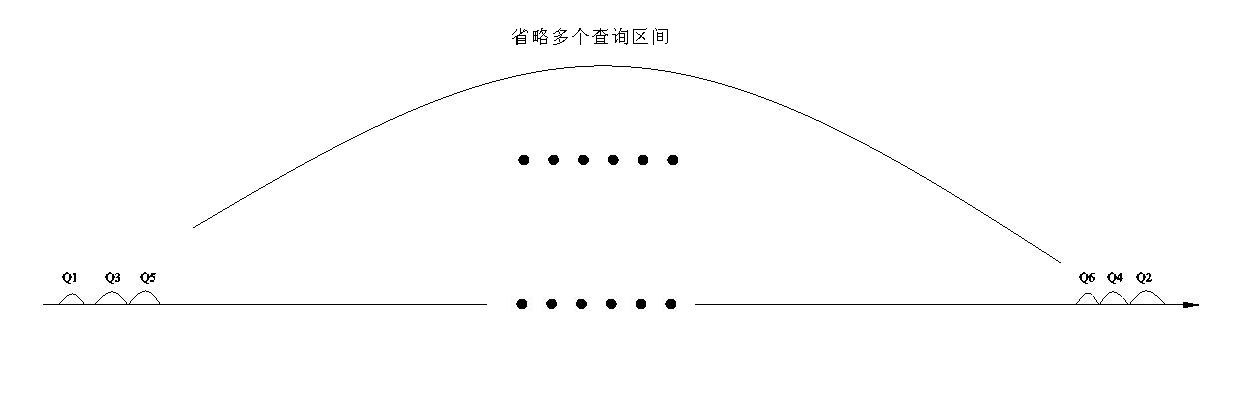
所以我们还需将查询区间的左端点进行排序。
(mathcal{Code})
#include<bits/stdc++.h>
using namespace std;
const int N = 3e4 + 10, M = 2e6 + 10;
int n, m, now, be[M], a[M], cnt[M], ans[M];
struct Node {
int l, r, id;
} q[M];
inline int read() {
int x = 0, k = 1; char c = getchar();
for (; c < 48 || c > 57; c = getchar()) k ^= (c == '-');
for (; c >= 48 && c <= 57; c = getchar()) x = x * 10 + (c ^ 48);
return k ? x : -x;
}
inline bool cmp(Node a, Node b) { // 奇偶性排序
return (be[a.l] ^ be[b.l]) ? be[a.l] < be[b.l] : ((be[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
int main() {
n = read();
int sz = sqrt(n), n1 = ceil((double)n / sz);
for (int i = 1; i <= n1; i++) // 分块
for (int j = (i - 1) * sz + 1; j <= i * sz; j++)
be[j] = i;
for (int i = 1; i <= n; i++)
a[i] = read();
m = read();
for (int i = 1; i <= m; i++)
q[i].l = read(), q[i].r = read(), q[i].id = i;
std::sort(q + 1, q + 1 + m, cmp);
int L = 1, R = 0;
for (int i = 1; i <= m; i++) {
int l = q[i].l, r = q[i].r;
while (L < l)
now -= !--cnt[a[L++]];
while (L > l)
now += !cnt[a[--L]]++;
while (R < r)
now += !cnt[a[++R]]++;
while (R > r)
now -= !--cnt[a[R--]];
ans[q[i].id] = now;
}
for (int i = 1; i <= m; i++)
printf("%d
", ans[i]);
return 0;
}
[国家集训队]小Z的袜子
(mathcal{Description})
给出一个长度为 (n) 的数列,有 (q) 个询问,需要求出在 ([l, r]) 区间内随机取出两个数数字一样的概率,若该概率为 (0) 则输出 (0/1) ,否则输出的 (A/B) 必须为最简分数。如果 (l == r) 则输出 (0 / 1)。
(mathcal{Solution})
基本与上面一题一样。
取到两个相同的数的方案数为 (frac{sum _ {i = 1} ^ {N} (cnt[i] - 1) * cnt[i]}{2} (cnt[i] geq 2))
总方案数为 (frac {(r - l + 1) * (r - l)}{2})
(mathcal{Code})
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 10, M = 5e6 + 10;
int n, m, now, be[M], a[M], cnt[N], ansx[M], ansy[M];
struct Node {
int l, r, id;
} q[M];
inline int read() {
register int x = 0, k = 1; char c = getchar();
for (; c < 48 || c > 57; c = getchar()) k ^= (c == '-');
for (; c >= 48 && c <= 57; c = getchar()) x = x * 10 + (c ^ 48);
return k ? x : -x;
}
inline void print(int x) {
if(x / 10) print(x / 10);
putchar(x % 10 + '0');
}
inline bool cmp(Node a, Node b) {
return (be[a.l] != be[b.l]) ? be[a.l] < be[b.l] : ((be[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
signed main() {
int n = read();
m = read();
register int sz = sqrt(n);
for (register int i = 1; i <= n; i++)
a[i] = read(), be[i] = i / sz + 1;
for (register int i = 1; i <= m; i++)
q[i].l = read(), q[i].r = read(), q[i].id = i;
std::sort(q + 1, q + 1 + m, cmp);
register int L = 1, R = 0, l, r;
for (register int i = 1; i <= m; i++) {
l = q[i].l, r = q[i].r;
if (l == r) {
ansx[q[i].id] = 0, ansy[q[i].id] = 1;
continue;
}
while (L > l) {
L--;
now -= cnt[a[L]] * (cnt[a[L]] - 1);
cnt[a[L]]++;
now += cnt[a[L]] * (cnt[a[L]] - 1);
}
while (L < l) {
now -= cnt[a[L]] * (cnt[a[L]] - 1);
cnt[a[L]]--;
now += cnt[a[L]] * (cnt[a[L]] - 1);
L++;
}
while (R > r) {
now -= cnt[a[R]] * (cnt[a[R]] - 1);
cnt[a[R]]--;
now += cnt[a[R]] * (cnt[a[R]] - 1);
R--;
}
while (R < r) {
R++;
now -= cnt[a[R]] * (cnt[a[R]] - 1);
cnt[a[R]]++;
now += cnt[a[R]] * (cnt[a[R]] - 1);
}
ansx[q[i].id] = now;
ansy[q[i].id] = (q[i].r - q[i].l + 1) * (q[i].r - q[i].l);
}
for (register int i = 1; i <= m; i++) {
if (!ansx[i]) {
printf("0/1
");
continue;
}
int d = __gcd(ansx[i], ansy[i]);
printf("%lld/%lld
", ansx[i] / d, ansy[i] / d);
}
return 0;
}
小清新人渣的本愿
(mathcal{Description})
给出一个长度为 (n) 的数列,有 (q) 个询问,每次询问给出 (opt)、(l)、(r)、(x)。
1、若 (opt) 为 (1), 询问一个区间是否可以选出两个数差为 (x)。
2、若 (opt) 为 (2), 询问一个区间是否可以选出两个数和为 (x)。
1、若 (opt) 为 (3), 询问一个区间是否可以选出两个数乘积为 (x)。
对于每个询问,如果可以,输出hana,如果不可以,输出bi。
(mathcal{Solution})
如果想学 (bitset) 可以进这个链接。
当然本题只需要知道一些很基础的。
用 (bitset) 维护,每一位表示每个数字是否存在,记为(now1)。
若 (opt == 1),如果存在 (z - y = x), 则必存在 (z) 和 (z - x)。
若 (opt == 2),就是求 (z + y = x),所以除 (now1) 外,我们还需用 (bitset) 记录一个 (now1) 的反串,就是每一位 (i) 都表示 (N - i)。问题就转化成满足 (now1) 中有 (z) 和 (now2) 中有 (y^{'})。代入 (z + y = x) 中,得到 (z + N - y ^ {'} = x),(z - y ^ {'} = x - N)。
若 (opt == 3),直接枚举约数。
(mathcal{Code})
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2e6 + 10;
int n, m, now, be[M], a[M], cnt[M], ans[M];
bitset <N + 10> now1, now2;
struct Node {
int l, r, id, k, x;
} q[M];
inline int read() {
int x = 0, k = 1; char c = getchar();
for (; c < 48 || c > 57; c = getchar()) k ^= (c == '-');
for (; c >= 48 && c <= 57; c = getchar()) x = x * 10 + (c ^ 48);
return k ? x : -x;
}
inline bool cmp(Node a, Node b) {
return (be[a.l] ^ be[b.l]) ? be[a.l] < be[b.l] : ((be[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
inline void del(int x) {
if (--cnt[x] == 0)
now1[x] = now2[N - x] = 0;
}
inline void add(int x) {
if (cnt[x]++ == 0)
now1[x] = now2[N - x] = 1;
}
int main() {
n = read(), m = read();
int sz = sqrt(n), n1 = ceil((double)n / sz);
for (int i = 1; i <= n1; i++)
for (int j = (i - 1) * sz + 1; j <= i * sz; j++)
be[j] = i;
for (int i = 1; i <= n; i++)
a[i] = read();
for (int i = 1; i <= m; i++)
q[i].k = read(), q[i].l = read(), q[i].r = read(), q[i].x = read(), q[i].id = i;
std::sort(q + 1, q + 1 + m, cmp);
int L = 1, R = 0;
for (int i = 1; i <= m; i++) {
int l = q[i].l, r = q[i].r, k = q[i].k, x = q[i].x;
while (L < l)
del(a[L++]);
while (L > l)
add(a[--L]);
while (R < r)
add(a[++R]);
while (R > r)
del(a[R--]);
if (k == 1) {
if ((now1 & (now1 << x)).any()) {
ans[q[i].id] = 1;
continue;
}
}
if (k == 2) {
if ((now1 & (now2 >> (N - x))).any()) {
ans[q[i].id] = 1;
continue;
}
}
if (k == 3) {
for (int j = 1; j * j <= x; j++)
if ((!(x % j)) && (now1[j] && now1[x / j])) {
ans[q[i].id] = 1;
continue;
}
}
}
for (int i = 1; i <= m; i++)
if (!ans[i])
puts("bi");
else
puts("hana");
return 0;
}
带修莫队
[国家集训队]数颜色 / 维护队列
(mathcal{Description})
给出一个长度为 (n) 的数列,有 (q) 个操作。
1、(Q) (l) (r) 代表询问 ([l, r]) 有多少不同的数。
2、(C) (P) (Col) 代表把第 (P) 个数变成 (Col)。
(mathcal{Solution})
对于带修莫队,实际上就是在原来普通莫队上加上一个时间戳。于是当前区间移动方向就由四个([l - 1, r])、([l + 1, r])、([l, r - 1])、([l, r + 1])变为六个([l - 1, r, t])、([l + 1, r, t])、([l, r - 1, t])、([l, r + 1, t])、([l, r, t - 1])、([l, r, t + 1])。
(mathcal{Code})
#include<bits/stdc++.h>
using namespace std;
const int N = 3e4 + 10, M = 2e6 + 10;
int n, m, now, be[M], a[M], cnt[M], ans[M], cntc, cntq;
char ch;
struct Query {
int l, r, id, time;
} q[M];
struct Replace {
int pos, color;
} c[M];
inline int read() {
int x = 0, k = 1; char c = getchar();
for (; c < 48 || c > 57; c = getchar()) k ^= (c == '-');
for (; c >= 48 && c <= 57; c = getchar()) x = x * 10 + (c ^ 48);
return k ? x : -x;
}
inline bool cmp(Query a, Query b) {
return (be[a.l] ^ be[b.l]) ? be[a.l] < be[b.l] : ((be[a.r] ^ be[b.r]) ? be[a.r] < be[b.r] : a.time < b.time);
}
int main() {
n = read(), m = read();
int sz = pow(n, 2.0 / 3.0), n1 = ceil((double)n / sz);
for (int i = 1; i <= n1; i++)
for (int j = (i - 1) * sz + 1; j <= i * sz; j++)
be[j] = i;
for (int i = 1; i <= n; i++)
a[i] = read();
for (int i = 1; i <= m; i++) {
scanf("%c", &ch);
while (ch != 'Q' && ch != 'R')
scanf("%c", &ch);
if (ch == 'Q') {
q[++cntq].l = read(), q[cntq].r = read(), q[cntq].time = cntc, q[cntq].id = cntq;
}
else if (ch == 'R') {
c[++cntc].pos = read(), c[cntc].color = read();
}
}
std::sort(q + 1, q + 1 + cntq, cmp);
int L = 1, R = 0, Time = 0;
for (int i = 1; i <= m; i++) {
int l = q[i].l, r = q[i].r, time = q[i].time;
while (L < l)
now -= !--cnt[a[L++]];
while (L > l)
now += !cnt[a[--L]]++;
while (R < r)
now += !cnt[a[++R]]++;
while (R > r)
now -= !--cnt[a[R--]];
while (Time < time) {
Time++;
if (l <= c[Time].pos && r >= c[Time].pos)
now -= !--cnt[a[c[Time].pos]] - !cnt[c[Time].color]++;
std::swap(a[c[Time].pos], c[Time].color);
}
while (Time > time) {
if (l <= c[Time].pos && r >= c[Time].pos)
now -= !--cnt[a[c[Time].pos]] - !cnt[c[Time].color]++;
std::swap(a[c[Time].pos], c[Time].color);
Time--;
}
ans[q[i].id] = now;
}
for (int i = 1; i <= cntq; i++)
printf("%d
", ans[i]);
return 0;
}