排序算法-归并排序

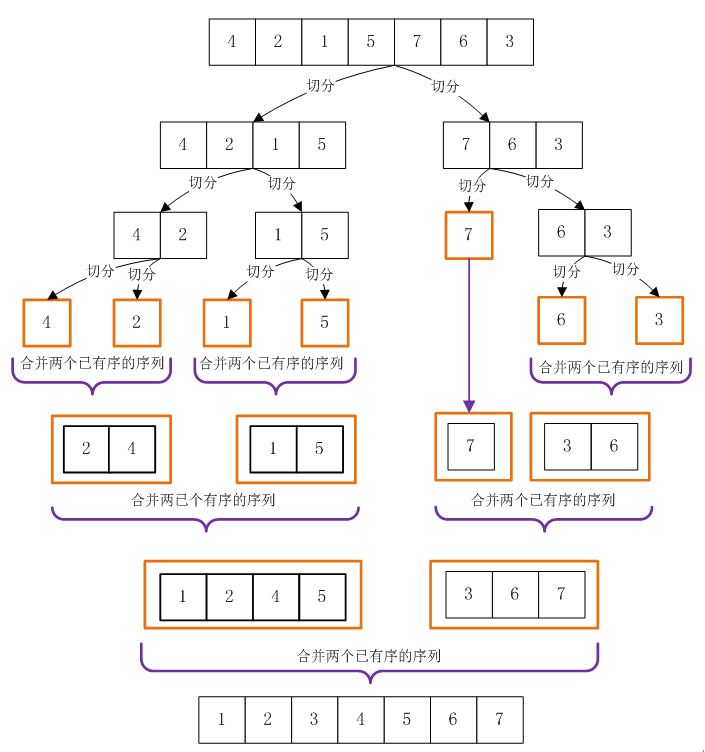
自顶向下的递归

归并排序的思想是先二分数组，然后再对每一部分进行二分，最后递归至每一部分只有一个元素，然后再进行组合。

优点：速度快

缺点：空间消耗较大

实现步骤：三个函数，一个总接口调用函数，一个递归函数，一个归并函数

//归并排序部分
public void merageSort(Integer[] arr,Integer n){
    __meargeSort(arr,0,n-1);
}
    //归并算法，递归部分
public void __meargeSort(Integer[] arr,Integer l,Integer r){
    if(l>=r) return;
    Integer middle = (l+r)/2;
    __meargeSort(arr,l,middle);
    __meargeSort(arr,middle+1,r);
    __meargeResult(arr,l,middle,r);
}
    //归并算法，数据合并部分
public void __meargeResult(Integer[] arr,Integer l,Integer middle,Integer r){
    //拷贝原数组，以便进行对比
    Integer[] re = new Integer[r-l+1];
    for(int i =0;i<r-l+1;i++){
        re[i] = arr[i+l];
    }
    //i代表左侧数组，j代表右侧数组
    int i =l,j=middle + 1;
    for(int k =l;k<=r;k++){
        //左侧数据结束了，右侧没有结束
        if(i>middle){
            arr[k] = arr[j-l];
            j++;
        }
        //右侧数组结束了，左侧还没有结束
        else if(j>r){
            arr[k] = re[i-l];
            i++;
        }//左侧小于右侧，复制后指针+1
        else if(re[i-l]<re[j-l]){
            arr[k]=re[i-l];
            i++;
        }//右侧小于左侧
        else{
            arr[k] = re[j-l];
            j++;
        }
    }

}

优化一：数据近乎是有序数据时：

　　当middle的值大于middle+1位置的值时，认为需要排序，否则跳过

    //归并算法，递归部分
public void __meargeSort(Integer[] arr,Integer l,Integer r){
    if(l>=r) return;
    Integer middle = (l+r)/2;
    __meargeSort(arr,l,middle);
    __meargeSort(arr,middle+1,r);
　　if(arr[middle]>arr[middle+1]){
    　　__meargeResult(arr,l,middle,r);
　　}
}

　

优化二：当数组个数小于15时，采用插入排序性能更好

//归并排序部分
public void merageSort(Integer[] arr,Integer n){
    __meargeSort(arr,0,n-1);
}
    //归并算法，递归部分

public void __meargeSort(Integer[] arr,Integer l,Integer r){

    if(r-l<=15) {__meargeInsertSort(arr,l,r); return;}
    Integer middle = (l+r)/2;
    __meargeSort(arr,l,middle);
    __meargeSort(arr,middle+1,r);
    if(arr[middle]>arr[middle+1]){
        __meargeResult(arr,l,middle,r);
    }
}

//归并算法的插入排序
public void __meargeInsertSort(Integer[] arr,Integer l,Integer r){
    for(int i =l+1;i<=r;i++){
        Integer temp = arr[i];
        int j;
        for(j=i;j>l && arr[j-1]>temp;j--){
            arr[j] = arr[j-1];
        }
        arr[j] =temp;
    }
}
    //归并算法，数据合并部分
public void __meargeResult(Integer[] arr,Integer l,Integer middle,Integer r){
    //拷贝原数组，以便进行对比
    Integer[] re = new Integer[r-l+1];
    for(int i =0;i<r-l+1;i++){
        re[i] = arr[i+l];
    }
    //i代表左侧数组，j代表右侧数组
    int i =l,j=middle + 1;
    for(int k =l;k<=r;k++){
        //左侧数据结束了，右侧没有结束
        if(i>middle){
            arr[k] = arr[j-l];
            j++;
        }
        //右侧数组结束了，左侧还没有结束
        else if(j>r){
            arr[k] = re[i-l];
            i++;
        }//左侧小于右侧，复制后指针+1
        else if(re[i-l]<re[j-l]){
            arr[k]=re[i-l];
            i++;
        }//右侧小于左侧
        else{
            arr[k] = re[j-l];
            j++;
        }
    }

}

自底向上的归并排序

 把数组划分成一个小段一个小段的，每两个划分为一组，然后排序，然后每四个一组，向上递归。

 

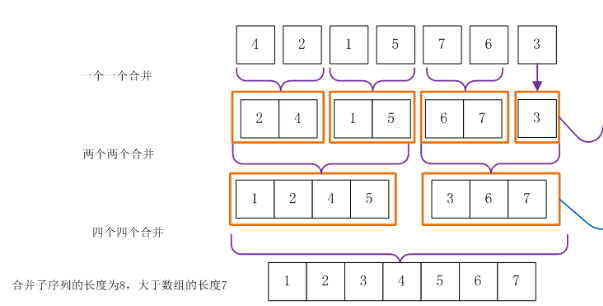
代码；

public void mergeSortDU(Integer[] arr,int n){
    //第一层循环是对归并大小进行控制，模拟递归过程
    for(int size = 1;size<n;size +=size){
        //第二层循环是对每次递归循环次数的控制，注意边界问题
        //i+size<n 确保i+size不越界，第一个归并数组有数据
        //第二个归并数组有数据Integer l = i+2*size>n-1?n-1:i+2*size;,确保第二部分不越界
        for(int i=0;i+size<n;i += size*2){
            Integer l = i+2*size>n-1?n-1:i+2*size;
            __mergeSortDU(arr,i,i+size-1,l);
        }
    }
}
public void __mergeSortDU(Integer[] arr,int l,int middle,int r){
    //临时空间
    Integer[] aux = new Integer[r-l+1];
    //赋值到临时空间
    for(int i=l;i<=r;i++) aux[i-l] = arr[i];
    int i =l,j=middle+1;
    for(int k=l;k<=r;k++){
        if(i>middle){ arr[k] = aux[j-l];j++;}
        else if(j>r){arr[k] = aux[i-l];i++;}
        else if(aux[i-l]>arr[j-l]){arr[k] = aux[j-l];j++;}
        else { arr[k] = aux[i-l];i++;}
    }
}