二.逻辑运算
逻辑与:∧(或‘·’)
逻辑或:∨ (或‘+’)
逻辑非:┐
优先级:逻辑非>逻辑与>逻辑或,有括号按括号,无括号先按优先级,同级运算从左至右
与位运算结合优先级:逻辑非(!,┐)=按位反(~)>位移运算(<<,>>)>不等号(>=,<=)>等号(==,!=)>按位与(&)>按位异或(^)>按位或(|)>逻辑与(&&,∧)>逻辑或(||,∨)
三.数据结构
1.二叉树
(1)二叉树的三种遍历方式:
①.先序遍历:根-左-右
②.中序遍历:左-根-右:
③.后序遍历:左-右-根
结论:给定中序遍历和先序遍历或后序遍历组合都可以确定这棵二叉树,但是给定先序遍历和后序遍历组合则不可确定
(2)二叉树特例:
完全二叉树:对于每个节点,都有两个子节点
满二叉树:对于每个节点,都有两个子节点且树完全“平衡”,总节点个数为2^k-1,k∈Z(如上面的样例)
(3)二叉树的有关公式:
一棵满二叉树:节点个数为,叶节点个数为
<其中k为树的高度
二叉树的深度均摊为log2n,其中n为节点个数(这就是treap等二叉搜索树时间复杂度的来源)
2.栈与队列
(1)栈:只有一个口,后进栈者先出栈
(2)队列:有head和tail,从尾入队,从头出队,先进先出
3.链表:
链表:每个元素会有一个指针指向要求的下一个元素
分类:
单向链表:每个元素只有一个指针指向下一个元素
双向链表:每个元素有两个指针,一个指向下一个元素,另一个指向指向他的元素
链表可以实现O(n)查询,O(1)删除(重构指针即可)
4.图论有关知识:
完全图:任意两点均有连边的图,其中边数为n*(n-1)/2,其中n为图中节点个数
连通图:任意两点之间都能直接或间接通过边到达的图
树:任意两点之间的简单路径有且仅有一条(或有n个点,n-1条边的连通图)
欧拉图:可以一笔画出来的图
一个图是欧拉图的充要条件(无向图):度为奇数点的点的个数<=2
相关定义:
欧拉环游:通过图中每边恰好一次的闭路径
欧拉闭迹:通过图中每边恰好一次的路径
三.IT基础知识与历史:
1.编程语言:
编程语言主要分两类:面向对象和面向过程
常见的面向对象高级语言:
simula 67,支持单继承和一定含义的多态和部分动态绑定;
Smalltalk,支持单继承、多态和动态绑定;
EIFFEL,支持多继承、多态和动态绑定;
C++,支持多继承、多态和部分动态绑定。
Java,支持单继承、多态和部分动态绑定。
结论:面向对象语言常见特点:封装,继承,多态
常见的面向过程高级语言:
C语言
Fortran语言
常见的低级语言:
汇编
高级语言与低级语言的区别:
高级语言更易移植,需要编译运行,低级语言(汇编)常数极小,运行速度快
2.计算机历史
对计算机做出重要贡献的人物:
图灵,冯·诺依曼(101页报告,EDVAC)
计算机的顶级奖项:
图灵奖
中国获图灵奖的人物:
姚期智
第一台计算机:
ENIAC
第一台具有存储程序功能的计算机:
EDVAC
3.计算机硬件原理问题:
微型计算机的面世——超大规模集成电路
计算机存储:
常见存储设备:ROM,RAM,硬盘,U盘,内存
四.实际问题的解决:
1.常见递推问题:
平面分割问题:
n条直线最多将平面分成的部分:
推广:n个平面最多将空间分成的部分:
n条封闭曲线最多将平面分成的部分: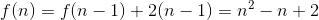
n条折线最多将平面分成的部分: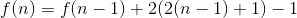
n条‘Z’型折线最多将平面分成的部分:
斐波那契数列问题: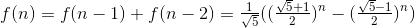
卡特兰数列问题: