我们经常会遇到一些与求{1,2,...,n}的排列等价的问题。为了解决这些问题,我们需要生成{1,2,…,n}的全部排列或找出某一个特定的排列。本文介绍一些常见的排列生成算法,给出它们的C(或C++)实现。其中一些算法是根据已有经验编写的,其他的算法是在已知的经典算法的基础上略作改动得到的。
为了实现全排列生成算法,我们需要定义一些基本的操作如交换(interchange)、反序(reverse)和打印(print)。A-0是这些操作的C(或C++)描述。
A-0
1 #include <stdio.h> 2 3 // interchange set[i] <-> set[j] 4 void interchange(int set[], int i, int j) { 5 int temp = set[i]; 6 set[i] = set[j]; 7 set[j] = temp; 8 } 9 10 // reverse set[i] ... set[j] 11 void reverse(int set[], int i, int j) { 12 int lim = i + (j - i) / 2; 13 for (int k = i; k <= lim; k++) { 14 interchange(set, k, j - k + i); 15 } 16 } 17 18 // print a array of integers in a line 19 void print(int set[], int n) { 20 for (int i = 0; i < n; i++) { 21 printf("%d ", set[i]); 22 } 23 printf(" "); 24 }
1. 字典序排列生成算法
在全排列生成算法中,最常用的是字典序全排列生成算法。将两个不同的排列p1和p2中的元素从左到右依次比较, 若p1中某一元素比p2中同一位置的元素大,那么就认为按字典序p1比p2大。例如 {1,2, 3}的两个排列 1 2 3 和 1 3 2, 从左到右依次比较,由于在两个排列的第二个位置上 2 < 3, 所以排列 1 2 3 字典序小于 1 3 2。{1, 2, 3} 的字典序全排列为:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
后面几个小节将介绍字典序全排列生成算法。
1.1 回溯法
回溯法(backtracking)可能是最容易想到的全排列生成算法。回溯法是对蛮力算法(the brute force approach)的一种改进。回溯法通常会有如下模式:

A-1是套用上面模式的字典序全排列生成算法的C(或C++)语言实现。bt_generate(0)以字典序从小到大打印 {0, 1, ..., N - 1} 的所有排列,其中N是一个宏定义,在示例程序中其值为4。A-1是典型的蛮力解法,其时间复杂度为O(nn+1),它检查所有的nn(n为数据规模,在上述程序中n = N)个可能的长度为n的向量,将其中的{0, 1,..., n - 1} 的排列打印出来。其中检查函数is_valid() 的时间复杂度为O(n)。算法A-1 的空间复杂度为O(n)。
A-1
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define MAX_SIZE 16 5 6 int vector[MAX_SIZE]; 7 int end = -1; 8 9 #define is_empty() (end == -1) 10 #define push_back(v) (vector[++end] = v) 11 #define pop_back() (vector[end--]) 12 13 void print_vector() { 14 int i; 15 for (i = 0; i <= end; i++) { 16 printf("%d ", vector[i]); 17 } 18 printf(" "); 19 } 20 21 int is_valid() { 22 int* used = 23 (int*) malloc((end + 1) * sizeof(int)); 24 int i; 25 26 for (i = 0; i <= end; i++) { 27 used[i] = 0; 28 } 29 for (i = 0; i <= end; i++) { 30 used[vector[i]] = 1; 31 } 32 for (i = 0; i <= end; i++) { 33 if (used[i] == 0) 34 break; 35 } 36 free(used); 37 38 if (i > end) 39 return 1; 40 return 0; 41 } 42 43 #define N 4 44 45 // call bt_generate1(0) to generate all permutations of {0, 1, ... , N1 - 1} in 46 // loxicographic order 47 void bt_generate(int n) { // O(n^n) 48 if (n == N) { 49 if (is_valid()) 50 print_vector(); // print a valid permutation 51 } else { 52 int i; 53 for (i = 0; i < N; i++) { 54 push_back(i); 55 bt_generate(n + 1); 56 pop_back(); 57 } 58 } 59 }
可以对A-1中的算法改进,让它运行得更快一些。A-2是改进后的算法的C(或C++)语言版本。通过调用bt_generate(0)就可以以字典序打印 {0, 1, ..., N-1}的全部排列。不难看出,A-2比A-1具有更小的时间复杂度,其时间复杂度为O(n*n!)。A-2的空间复杂度为O(n)。
A-2
1 #define N 4 2 3 int p[N], used[N] = {0}; 4 5 // call bt_generate(0) to print all permutations of {0, 1, ... , N - 1} 6 // in loxicographic order 7 void bt_generate(int n) { 8 if (n == N) { // indicate a valid permutation 9 print(p, N); // print p[0] p[1] ... p[N – 1] 10 return; 11 } 12 13 for (int i = 0; i < N; i++) { 14 if (used[i] == 0) { 15 used[i] = 1; 16 p[n] = i; 17 bt_generate(n + 1); 18 used[i] = 0; 19 } 20 } 21 }
1.2 基于交换的算法
A-3是一个经典的排列生成算法,这个算法在O(n)时间内就可以得到在字典序中一个排列的下一个排列。利用这个算法,我们可以在O(n*n!)时间内得到 {set[0],set[1],..., set[n-1]}的全部排列,在这里并不要求set[0],set[1],...,set[n-1] 两两互不相同。值得注意的是,函数lex_next_perm返回的是一个bool类型的值。这个返回值指示输入是否是字典序的最后一个排列,若是,返回值为false, 否则,返回值为true。若输入为字典序的最后一个排列,当函数返回时,保存在set[]中的将是字典序最小的排列。
算法A-3对应的伪代码(逻辑上有所改动)如下:

A-3
1 /* -------------------- lexicographic permutation generation ------------------ */ 2 3 // retrieve the next permutation of a certain permutation 4 bool lex_next_perm(int set[], int n) { // Algoriym Complexity : O(n) 5 if (n > 0) { // if the perameters are valid 6 // find max{ j | j >= 0 && j < n - 1 && set[j] < set[j + 1] } 7 int j; 8 for (j = n - 2; j >= 0; j--) { 9 if (set[j] < set[j + 1]) 10 break; 11 } 12 13 if (j == -1) { // indicate the last permutation 14 reverse(set, 0, n - 1); 15 return false; 16 } else { 17 // find max{ l | l > j && l < n && set[l] > set[j] } 18 int l; 19 for (l = n - 1; l > j; l--) { 20 if (set[l] > set[j]) 21 break; 22 } 23 interchange(set, j, l); // interchange set[j] <-> set[l] 24 reverse(set, j + 1, n - 1); // reverse set[j+1] ... set[n-1] 25 } 26 return true; 27 } 28 29 return false; 30 } 31 32 /* ---------------------------------------------------------------------------- */
1.3 生成一个特定的排列的算法
我们有时候需要得到字典序全排列中某一特定的排列。我们将字典序排列编号,从0到n!-1,我们需要一种方法能够得到第i 个排列(或编号为i的排列)。程序段A-4是得到字典序中第 i 个排列的C++语言代码。函数get_permutation的第一参数offset为所需要得到的排列在字典序中的编号,第二个参数set[]为一个由n(第三个参数)个不同的整数构成的数组,要求这些整数升序排列。函数将计算的结果保存在set[]中。该算法的时间复杂度为O(n2)。为了实现算法,需要计算n!,在这里我们通过查表的方法来得到n!。由于C++语言基本数据类型int表示范围的限制,该算法支持的数据规模不会很大。在A-4的实现中输入序列的长度不能超过11。
A-4
1 int factorial[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800}; 2 3 // get the offset-th permutation in lexicopraphic order 4 // set[] is a array of n distinct integers in ascending order 5 // the result holds in set[] 6 void get_permutation(int offset, int set[], int n) { 7 8 int fact = factorial[n]; 9 offset = (offset % fact + fact) % fact; 10 11 // assume that p[] is the permutation that this function is about to
// evaluate. aux[] is an auxiliary array in which aux[i] is the number 12 // of indices k > i such that p[k] < p[i] 13 int* aux = new int[n]; 14 int* copy = new int[n]; // a copy of the original array set[] 15 for (int i = n - 1; i >= 0; i--) { 16 aux[n - i - 1] = offset / factorial[i]; // initialize aux[] 17 offset %= factorial[i]; 18 copy[i] = set[i]; // do copy 19 } 20 21 // evaluate the offset-th permutaion 22 for (int i = 0; i < n; i++) { 23 int j = aux[i], k, s; 24 for (k = 0, s = 0; k < i; k++) { 25 if (set[k] <= copy[j]) { 26 s++; 27 } 28 } 29 j += s; 30 while (true) { 31 for (k = 0; k < i; k++) { 32 if (set[k] == copy[j]) { 33 j++; 34 break; 35 } 36 } 37 if (k == i) { 38 set[i] = copy[j]; // the i-th element in the permutation 39 break; 40 } 41 } 42 } 43 44 // release memory 45 delete[] aux; 46 delete[] copy; 47 }
2. Steinhaus-Johnson-Trotter 算法
Steinhaus-Johnson-Trotter算法或Johnson-Trotter算法,也叫Plain Changes算法。这一算法仅仅通过交换一个排列的相邻的两个元素来得到这个排列的下一个排列。算法要求排列的所有元素两两互不相同。这一算法简单并且具有低的时间复杂度。
值得注意的是,Steinhaus-Johnson-Trotter 算法得到的全排列并不是字典序的。
在Donald E. Knuth的著作《The Art of Computer Programming》的第7.2.1.2节给出了Plain Changes算法的伪代码。伪代码如下:

代码A-5是该算法的一个C++语言实现。在这段代码中所有的序列的下标是从0开始的。函数pc_all_perms的输入是一个包含按升序排列的n个不同的整数的数组。调用pc_all_perms将打印set[] 中所有元素的全排列。 代码段

将打印{1,2,3,4}的全部排列,输出结果如下:
1 2 3 4
1 2 4 3
1 4 2 3
4 1 2 3
4 1 3 2
1 4 3 2
1 3 4 2
1 3 2 4
3 1 2 4
3 1 4 2
3 4 1 2
4 3 1 2
4 3 2 1
3 4 2 1
3 2 4 1
3 2 1 4
2 3 1 4
2 3 4 1
2 4 3 1
4 2 3 1
4 2 1 3
2 4 1 3
2 1 4 3
2 1 3 4
A-5
1 /* ----------- Plain Changes (Steinhaus-Johnson–Trotter Algorithm) ------------ */ 2 3 // print all permutations of a given set 4 // set[] is a array of n distinct integers in ascending order 5 void pc_all_perms(int set[], int n) { 6 7 int *c = new int[n]; // c[i] is the number of elements lying to the 8 // right of the i-th smallest element of set[] 9 // notice : i >= 0 && i < n 10 int *o = new int[n]; // o[i] governs the direction by which c[i] changes 11 for (int i = 0; i < n; i++) // initialize c[] and o[] 12 c[i] = 0, o[i] = 1; 13 14 int j = n - 1, s = 0; 15 print(set, n); // print the original set[] 16 while (true) { 17 int q = c[j] + o[j]; 18 if (q >= 0 && q != j + 1) { 19 interchange(set, j - c[j] + s, j - q + s); // interchange 20 print(set, n); // print a permutaion 21 22 c[j] = q; 23 j = n - 1, s = 0; 24 continue; 25 } 26 27 if (q == j + 1) { 28 if (j == 0) 29 break; // terminate the algorithm 30 else 31 s++; 32 } 33 34 o[j] = -o[j], j--; 35 } 36 37 // release memory 38 delete[] c; 39 delete[] o; 40 } 41 42 /* ---------------------------------------------------------------------------- */
在Richard A. Brualdi的著作《Introductory Conbinatorics》(中文版书名为《组合数学》)第五版的第四章4.1节给出了邻位对换生成全排列的另一种实现方法。
序列的每一个元素都有与它相关联的方向,向左或向右,可以通过在其上画一个向左或向右的箭头来表示。若一个元素e1的箭头指向另一个元素e2,且有e1 > e2,则称e1是可移动的(mobile)。如,对于序列
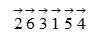
只有6、3和5是可移动的。于是,有如下算法:

我们以求1 2 3 4四个元素的全排列来说明该算法。算法的执行结果分两列显示,每一列有12个排列,第一列为前12个排列,第二列为后12个排列。

程序段A-6是上述算法的C++版本。函数ic_all_perms要求输入一个包含n个不同元素集合的升序排列set[]。它打印{set[0],set[1], ...,set[n-1]}的所有排列。该算法的时间复杂度为O(n∙n!)。
A-6
1 /* ------------- From Richard A. Brualdi : Introductory Conbinatorics --------- */ 2 3 #define LEFT 0 4 #define RIGHT 1 5 6 #define TRUE 1 7 #define FALSE 0 8 9 // Algorithm for generating the permutations of {set[0], ..., set[n - 1]} 10 // set[](input) is a array of n distinct integers in ascending order 11 void ic_all_perms(int set[], int n) { // print all permutations 12 13 int* direct = new int[n]; // the directions of the elements in set[] 14 int* mobile = new int[n]; // record whether set[i] is mobile 15 16 direct[0] = LEFT, mobile[0] = FALSE; // initialize direct[] and mobile[] 17 for (int i = 1; i < n; i++) { 18 direct[i] = LEFT; 19 mobile[i] = TRUE; 20 } 21 22 print(set, n); // print the original set[] 23 while(true) { 24 int i, i_max_mob; 25 26 //Does there exist a mobile integer in set[] ? 27 for (i = 0; i < n; i++) { 28 if (mobile[i] == TRUE) { 29 i_max_mob = i; 30 break; 31 } 32 } 33 if (i == n) // No mobile integers, Terminate the algorithm 34 break; 35 36 // get the index of the maximum mobile integer 37 for (i = i_max_mob + 1; i < n; i++) { 38 if (mobile[i] == TRUE && set[i] > set[i_max_mob]) 39 i_max_mob = i; 40 } 41 42 // switch the maximum mobile integer and the adjacent integer which 43 // its direction indicates 44 int k = i_max_mob + (direct[i_max_mob] == LEFT ? -1 : 1); 45 interchange(direct, i_max_mob, k); 46 interchange(set, i_max_mob, k); 47 print(set, n); // print the permutation 48 49 int m = set[k]; // the previous maximum mobile integer 50 // switch the direction of all integers set[i] with set[i] > m 51 for (i = 0; i < n; i++) { 52 if (set[i] > m) { 53 direct[i] = (direct[i] == LEFT ? RIGHT : LEFT); 54 } 55 } 56 57 // update mobile[] 58 for (i = 0; i < n; i++) { 59 if (i == 0 && direct[i] == LEFT 60 || i == n - 1 && direct[i] == RIGHT) 61 mobile[i] = FALSE; 62 else { 63 int adj = i + (direct[i] == LEFT ? -1 : 1); 64 if (set[i] > set[adj]) 65 mobile[i] = TRUE; 66 else 67 mobile[i] = FALSE; 68 } 69 } 70 } 71 72 // release memory 73 delete[] direct; 74 delete[] mobile; 75 } 76 77 /* ---------------------------------------------------------------------------- */
在维基百科(Wikipedia)上,有Shimon Even对Plain Changes改进后的算法。我们对该算法做一些改动,但基本思想保持不变。

该算法的时间复杂度为O(n∙n!)。
A-7给出了这一算法的C++描述。调用函数se_all_perms将打印{set[0], set[1],... , set[n-1]}(set[0],set[1], ..., set[n-1]两两互不相同)的全部排列。
A-7
1 /* ------------------------- Shimon Even's Solution --------------------------- */ 2 3 /** 4 * From the website: 5 * http://en.wikipedia.org/wiki/Steinhaus-Johnson-Trotter_algorithm 6 * 3 Even's speedup 7 */ 8 9 // Algorithm for generating the permutations of {set[0], ..., set[n - 1]} 10 // set[](input) is a array of n distinct integers in ascending order 11 void se_all_perms(int set[], int n) { // print all permutations 12 13 // the directions of the elements in set[]. each direct[i] is -1, 0, or 1 14 int* direct = new int[n]; 15 16 // initialize direct[] 17 direct[0] = 0; 18 for (int i = 1; i < n; i++) { 19 direct[i] = -1; 20 } 21 22 print(set, n); // print the original set[] 23 while(true) { 24 int i, i_max_nz; 25 26 // Does there exist a element with a nonzero direction ? 27 for (i = 0; i < n; i++) { 28 if (direct[i] != 0) { 29 i_max_nz = i; 30 break; 31 } 32 } 33 if (i == n) // No, terminate the algorithm 34 break; 35 36 // find the largest element with a nonzero direction 37 for (i = i_max_nz + 1; i < n; i++) { 38 if (direct[i] != 0 && set[i] > set[i_max_nz]) 39 i_max_nz = i; 40 } 41 42 // switch the largest nonzero-direction element in the indicated direction 43 int k = i_max_nz + direct[i_max_nz]; 44 interchange(direct, i_max_nz, k); // direct[i_max_nz] <-> direct[k] 45 interchange(set, i_max_nz, k); // set[i_max_nz] <-> direct[k] 46 print(set, n); // print the permutation 47 48 // get the previous largest element with non-zero direction 49 int m = set[k]; 50 // update direct[] 51 for (i = 0; i < n; i++) { 52 if (i == 0 && direct[i] == -1 53 || i == n - 1 && direct[i] == 1) 54 direct[i] = 0; 55 else if (direct[i] == 0 && set[i] > m) { 56 direct[i] = (k - i > 0 ? 1 : -1); 57 } 58 } 59 } 60 61 // release memory 62 delete[] direct; 63 } 64 65 /* ---------------------------------------------------------------------------- */
3. 总结
本文描述了一些全排列生成算法。当然,全排列生成算法不止这些。在本文列举的全排列生成算法中,在不考虑打印每一个排列的开销的情况下,算法的时间复杂度最好是O(n!)。此外,我们可以在O(n)时间里得到一个排列在字典序中的下一个排列,在O(n2)时间获得字典序编号为i的排列。
4. 参考文献
[1] http://www.cse.ohio-state.edu/~gurari/course/cis680/cis680Ch19.html.
[2] Donald E. Knuth. The Art of Computer Programming Volume 4. A Draft of Section
7.2.1.2: Generating All Permutations.
[3] Richard A. Brualdi. Introductory Cobinatorics. China Machine Press, Fifth edition, 2009.
[4] http://en.wikipedia.org/wiki/Steinhaus-Johnson-Trotter_algorithm.