• C++排序算法小结

         近期来闲来无事，整理了一些比较常见的排序算法，都是用C++写的，其中包括：直接插入排序、折半插入排序、冒泡排序、选择排序、快速排序、堆排序、归并排序、希尔排序、基数排序，计数排序和桶排序，总共11种算法，其中时间复杂度为O(n^2)为前4种，中间4中的时间复杂度为O(nlgn)，最后3种的时间复杂度为O(n)。下面我们分3个栏目来介绍:n^2排序、nlgn排序和线性排序。

    注：A为全局变量，为一维int数组，N为数组元素个数

    n^2排序

    直接插入排序

         类似于扑克牌排序的原理，在斗地主的时候，每当摸到一张牌后就插入到相应的位置，直接插入排序就是这个原理。从数组第一个数开始，比较该数和前面的数的大小，如果前面的数比该数小，则和前面一位的数调换位置，然后继续比较，直到出现一个数比该数小为止。

         核心代码如下：

     1 void InsertSort()
 2 {
 3     int i,j;
 4     for(i = 1;i <= N;i++)
 5     {
 6         j = i;
 7         while(j > 0 && A[j] < A[j - 1])
 8         {
 9             swap(A[j],A[j-1]);
10             j --;
11         }
12     }    
13 }
    View Code

    折半插入排序

         其实这种算法是直接插入排序的一种优化，在一个数与其前面的数字进行比较的时候，取以数组第一个数和该数前一个数为区间的中间的数，类似与二分法。

    核心代码如下：

     1 void HalfSort()
 2 {
 3     int i, j, high, low, mid;
 4     for (i = 2; i <= N; i++)
 5     {
 6         A[0] = A[i];
 7         low = 1;
 8         high = i - 1;
 9         while (low <= high)
10         {
11             mid = (low + high) / 2;
12             if (A[0] < A[mid])
13                 high = mid - 1;
14             else
15                 low = mid + 1;
16         }
17         for (j = i - 1; j >= high + 1; j--)
18             A[j + 1] = A[j];
19         A[high + 1] = A[0];
20     }
21 }
    View Code

    冒泡排序

         这个排序算法算是我最早接触的算法，原理就是每次内循环一遍就能把最小的数排到前面，这样外循环完后就排好了。

    核心算法如下：

     1 void BubbleSort()
 2 {
 3     for(int i = 1;i <= N - 1;i++)
 4     {
 5         for(int j = N;j >= i+1;j--)
 6         {
 7             if(A[j] < A[j - 1])
 8                 swap(A[j],A[j-1]);
 9         }
10     }
11 }
    View Code

    选择排序

         和冒泡排序类似，只不过是先找到最小的数的下标，然后再置换到相应的位置。

    核心代码如下：

     1 void SelectSort()
 2 {
 3     int i,j,lowkey,lowindex;
 4     for(i = 1;i <= N - 1;i++)
 5     {
 6         lowindex = i;
 7         lowkey = A[i];
 8         for(j = i + 1;j <= N;j++)
 9         {
10             if(A[j]<lowkey)
11             {
12                 lowkey = A[j];
13                 lowindex = j;
14             }
15         }
16         swap(A[i],A[lowindex]);
17     }
18 }
    View Code

    nlgn排序

    快速排序

         这个排序算法在nlgn排序算法中算是比较常见的算法了，速度快而且可以进行不同程度的优化。

         算法原理概括为2部分：

         •分解：数组A[i..j]被划分为两个(可能为空)子数组A[i..q-1]和A[q+1..j]，使得A[i..q-1]中没一个元素都小于等于A[q]，而A[q]也小于等于A[q+1..j]中每一个元素。其中，计算下标q也是划分过程的一部分;

         •解决：通过递归调用快速排序，对子数组A[i..q-1]和A[q+1..j]进行排序;

         返回合适的主元下标，这里是用数组从左到右两个不同的数偏大的为主元：

     1 int FindPivot(int i,int j)
 2 {
 3     int firstkey = A[i];
 4     int k;
 5     for (k = i + 1; k <= j; k++)
 6     {
 7         if (A[k] > firstkey)
 8             return k;
 9         else if (A[k] < firstkey)
10             return i;
11     }
12     return 0;
13 }
    View Code

         划分部分代码：

     1 void Patition(int i, int j, int q)
 2 {
 3     int pivot = A[q];
 4     int l = i;
 5     int r = j;
 6     do
 7     {
 8            swap(A[l],A[r]);
 9     while(A[l] < pivot) l++;
10     while(A[r] >= pivot) r--;    
11     }while(l <= r);
12 }
    View Code

         排序代码：

     1 void QuickSort(int i, int j)
 2 {
 3     int q,l,r,pivot;
 4     q = FindPivot(i,j);
 5     if (q != 0)
 6     {
 7         Patition(i,j,q);
 8         QuickSort(i,l-1);
 9         QuickSort(l,j);
10     }
11 }
    View Code

         关于快排的优化问题，可以对两个点进行考虑，这里不贴具体代码：

         •主元的选择问题，可以采取随机数的方法

         •递归的时候，可以把所有与主元值一样的数字所在的数组下标都去掉，减少递归次数

    堆排序

         这里就用到了最大堆的相关概念，具体可以查看我的另一个博客：

         堆排序的原理是：用相关算法维持数组A的最大堆的性质的同时，然后每次取该数组的根(最大的数)，然后将其与最后的元素调换，再进行最大堆性质的维持，此时堆的元素个数减少一个，以此类推，则得到从小到大排列好的数组。

         维护堆的性质所需要的算法，它的输入为一个下标和堆此时元素个数，并且此时以根节点i的左右儿子为根节点的二叉树都是二叉树，但此时A[i]可能小于其儿子，这样就需要算法进行调整，如下：

     1 void MaxHeapify(int i,int heapsize)
 2 {
 3     int l = 2*i;
 4     int r = 2*i+1;
 5     int largest;
 6     if(l <= heapsize && A[l] > A[i])
 7         largest = l;
 8     else
 9         largest = i;
10     if(r <= heapsize && A[r] > A[largest])
11         largest = r;
12     if(largest != i)
13     {
14         swap(A[i],A[largest]);
15         MaxHeapify(largest,heapsize);
16     }
17 }
    View Code

         然后利用上面的算法建立一个数组A的最大堆：

    1 void BuildMaxHeap()
2 {
3     int heapsize = N;
4     for(int i = N/2;i > 0;i--)
5         MaxHeapify(i,heapsize);
6 }
    View Code

         最后就是堆排序算法：

     1 void HeapSort()
 2 {
 3     int heapsize = N;
 4     BuildMaxHeap();
 5     for(int i = N;i > 1;i--)
 6     {
 7         swap(A[1],A[i]);
 8         heapsize --;
 9         MaxHeapify(1,heapsize);
10     }
11 }
    View Code

    归并排序

         该算法采用了分治策略，即：

         •分解：分解待排序的n个元素的序列成各具n/2个元素的两个子序列;

         •解决：使用归并排序递归地排序两个子序列;

         •合并：合并两个已排序的子序列以产生已排序的答案。

         下面先进行对两个已经排好序的数组进行合并：

     1 void all_sort::Merge(int p,int q,int r)
 2 {
 3     int n1 = q - p + 1;
 4     int n2 = r - q;
 5     int *L = new int[n1+2];
 6     int *R = new int[n2+2];
 7     int i,j,k;
 8     for(i = 1;i <= n1;i++)
 9         L[i] = A[p+i-1];
10     for(i = 1;i <= n2;i++)
11         R[i] = A[q+i];
12             L[n1+1] = 10000;
13             R[n2+1] = 10000;
14     i = 1;
15     j = 1;
16     for(k = p;k <= r;k++)
17     {
18         if(L[i] <= R[j])
19         {
20             A[k] = L[i];
21             i ++;
22         }
23         else
24         {
25             A[k] = R[j];
26             j ++;
27         }
28     }
29 }
30
    View Code

         接着进行递归排序：

     1 void MergeSort(int p,int r)
 2 {
 3     int q;
 4     if(p<r)
 5     {
 6         q = (p+r)/2;
 7         MergeSort(p,q);
 8         MergeSort(q+1,r);
 9         Merge(p,q,r);
10     }
11 }
    View Code

    希尔排序

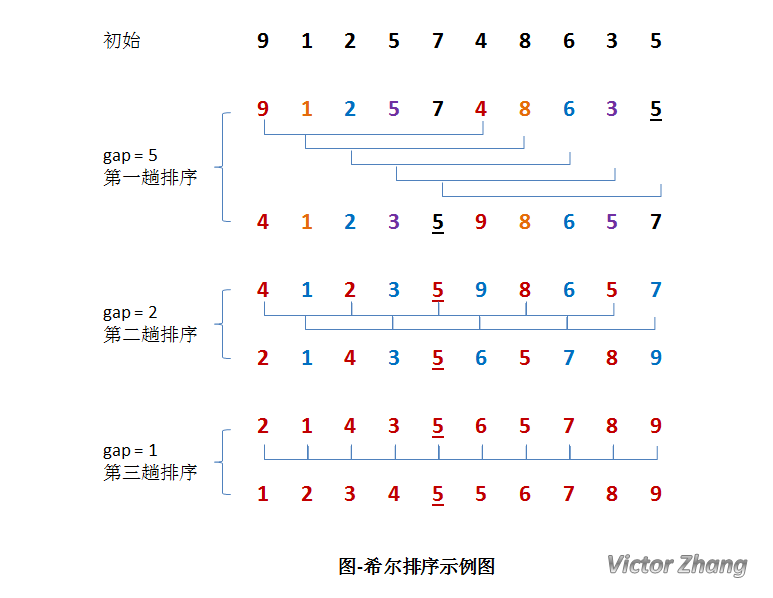
         该排序算法又称为缩小增量排序，其原理是：把数组A按照步长gap分组，对每组进行直接插入排序，随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序，以下为演示：

         核心代码如下：

     1 void shellSort()
 2 {
 3     int gap = N/2;
 4     int j,tmp;
 5     while(gap >= 1)
 6     {
 7         for(int i = gap+1;i <= N;i++)
 8         {
 9             tmp = A[i];
10             for(j = i - gap;j >= 1 && tmp < A[j];j = j - gap)
11                 A[j+gap] = A[j];
12             A[j+gap] = tmp;
13         }
14         gap = gap/2;
15     }
16 }
    View Code

    线性排序

    基数排序

         这种排序非常的聪明，利用10个桶编号0-9，然后从A数组中把数依次放入桶中。第一遍是按照数的个位数的值，若其等于桶的编号，则放入该桶，然后该数组的顺序就变成了从第0桶到第9桶的数的排列的顺序，再按照该顺序第二遍排序，先把各桶清空，按照每个数的十位数值放入相应桶中，接着是第三遍...第k遍，k为这些数中的最大位数。举例说明：

         •假设有欲排数据序列：73  22  93  43  55  14  28  65  39  81

         首先根据个位数的数值，在遍历数据时将它们各自分配到编号0至9的桶（个位数值与桶号一一对应）中：

        

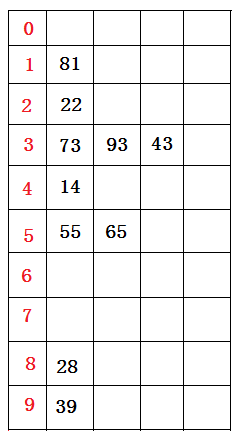
         •接着将所有桶中所盛数据按照桶号由小到大（桶中由顶至底）依次重新收集串起来，得到如下仍然无序的数据序列： 81  22  73  93  43  14  55  65  28  39

         接着，再进行一次分配，这次根据十位数值来分配（原理同上），分配结果（逻辑想象）如下图所示：

        

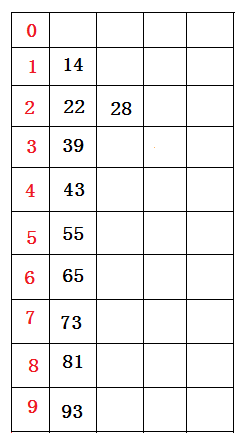
         分配结束后。接下来再将所有桶中所盛的数据（原理同上）依次重新收集串接起来，得到如下的数据序列：

         14  22  28  39  43  55  65  73  81  93

         •由于这些数中最大数的位数为2，故2遍就能得出排序后的序列。

         借助库函数<queue>，核心代码如下：

     1 int Radix(int k,int p)
 2 {
 3     int power, i;
 4     power = 1;
 5     for (i = 1; i <= p - 1; i++)
 6         power = power * 10;
 7     return ((k % (power * 10)) / power);
 8 }
 9 
10 void RadixSort()
11 {
12     queue<int> Q[10];
13     int data;
14     int pass, r, i;
15     for (pass = 1; pass <= 3; pass++)
16     {
17         while (!QA.empty())
18         {
19             data = QA.front();
20             QA.pop();
21             r = Radix(data, pass);
22             Q[r].push(data);
23         }
24         for (i = 0; i <= 9; i++)
25         {
26             while (!Q[i].empty())
27             {
28                 data = Q[i].front();
29                 Q[i].pop();
30                 QA.push(data);
31             }
32         }
33     }
34 }
    View Code

     计数排序

         计数排序假设n个输入元素的每一个都是在0到k区间的一个整数，其中k为某个整数。

         计数排序的基本思想是：对每一个输入元素x，确定小于x的元素个数。利用这一信息，就可以直接把x放到它在输出数组中的位置了。例如有17个元素小于x，则x的下标为17。当好几个元素相等时，要略微修改。

         核心代码如下(k为1000)：

     1 void CountingSort()
 2 {
 3     int C[1000];
 4     int i;
 5         //A_out存放排序的输出
 6     for(i = 0;i <=999;i++)
 7         C[i] = 0;
 8     for(i = 1;i <= N;i++)
 9         C[A[i]] ++;
10     for(i = 1;i <= 999;i++)
11         C[i] = C[i] + C[i-1];
12     for(i = N;i >= 1;i--)
13     {
14         A_out[C[A[i]]] = A[i];
15         C[A[i]] --;
16     }
17 }
    View Code

    桶排序

         桶排序假设输入数据服从均匀分布，假设输入是[0,1)的随机小数，桶排序将[0,1)区间划分为n个相同大小的子区间，然后，将n个输入数分别放入各个桶中。例如有100个无序小数序列，则建立0-99个桶，每个小数乘以100向下取整放入相应桶中，然后每个桶中的元素进行排序，就得到了完整的排好序的小数序列。

         伪代码如下：

     1 BucketSort()
 2 {
 3     let B[0..n-1] be a new array
 4     for i = 0 to N - 1
 5         make B[i] an empty list
 6     for i = 1 to N
 7         insert A[i] into list B[⌊nA[i]⌋]
 8     for i = 0 to N - 1
 9         sort list B[i] with insertion sort
10     concatenate the list B[0],B[1],...,B[n-1] together in order
11 }
    View Code

    作者: vachester
    出处：http://www.cnblogs.com/vachester/
    邮箱：xcchester@gmail.com
    本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接，否则保留追究法律责任的权利。

  • 相关阅读:
    day14(xml 编写及解析)
    day11(多线程,唤醒机制，生产消费者模式，多线程的生命周期)
    day13(反射，BeanUtils包)
    day10(IO流汇总)
    day08(File类 ，字节流)
    day08(异常处理，创建异常，finally，throws和throw的区别)
    [SPOJ-PT07J] Query on tree III (主席树)
    [ZJOI2008] 树的统计(树链剖分)
    长链剖分学习笔记
    [BZOJ4260] Codechef REBXOR (01字典树,异或前缀和)
  • 原文地址：https://www.cnblogs.com/vachester/p/5830150.html
Copyright © 2020-2023  润新知