ZeptoLab Code Rush 2015 B. Om Nom and Dark Park

B. Om Nom and Dark Park

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Om Nom is the main character of a game "Cut the Rope". He is a bright little monster who likes visiting friends living at the other side of the park. However the dark old parks can scare even somebody as fearless as Om Nom, so he asks you to help him.

The park consists of 2n + 1 - 1 squares connected by roads so that the scheme of the park is a full binary tree of depth n. More formally, the entrance to the park is located at the square 1. The exits out of the park are located at squares 2n, 2n + 1, ..., 2n + 1 - 1 and these exits lead straight to the Om Nom friends' houses. From each square i (2 ≤ i < 2n + 1) there is a road to the square 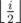. Thus, it is possible to go from the park entrance to each of the exits by walking along exactly n roads.

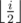To light the path roads in the evening, the park keeper installed street lights along each road. The road that leads from squarei to square  has ai lights.

Om Nom loves counting lights on the way to his friend. Om Nom is afraid of spiders who live in the park, so he doesn't like to walk along roads that are not enough lit. What he wants is that the way to any of his friends should have in total the same number of lights. That will make him feel safe.

He asked you to help him install additional lights. Determine what minimum number of lights it is needed to additionally place on the park roads so that a path from the entrance to any exit of the park contains the same number of street lights. You may add an arbitrary number of street lights to each of the roads.

Input

The first line contains integer n (1 ≤ n ≤ 10) — the number of roads on the path from the entrance to any exit.

The next line contains 2n + 1 - 2 numbers a2, a3, ... a2n + 1 - 1 — the initial numbers of street lights on each road of the park. Here ai is the number of street lights on the road between squares i and 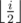. All numbers ai are positive integers, not exceeding 100.

Output

Print the minimum number of street lights that we should add to the roads of the park to make Om Nom feel safe.

Sample test(s)

input

2
1 2 3 4 5 6

output

5

Note

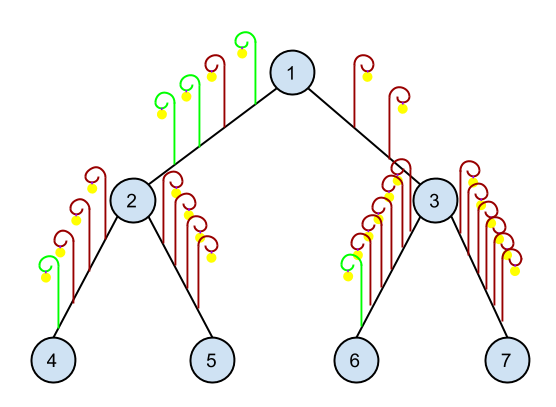
Picture for the sample test. Green color denotes the additional street lights.

题目大意：

　　就是说，给你一个二叉树，然后这个二叉树的每个边的权值都告诉你，你要做的就是从根节点开始遍历到每个叶子节点使得边的权值的和相等，如果不相等，我们应该怎样增加最小的灯的数目，使得最终的结果相等。

解题思路：

　　直接模拟就好了，每次从一对左右叶子节点开始，找到这两个叶子节点的父亲，然后用大的边权值减去小的边权值，得到一个数字，把这个数字更新到ans上面，然后把较大的边权值加到这个父亲节点到它父亲节点的权值上。

代码：

# include<cstdio>
# include<iostream>
# include<fstream>
# include<algorithm>
# include<functional>
# include<cstring>
# include<string>
# include<cstdlib>
# include<iomanip>
# include<numeric>
# include<cctype>
# include<cmath>
# include<ctime>
# include<queue>
# include<stack>
# include<list>
# include<set>
# include<map>

using namespace std;

const double PI=4.0*atan(1.0);

typedef long long LL;
typedef unsigned long long ULL;

# define inf 999999999
# define MAX 2333

int a[MAX];


int main(void)
{
    int n;cin>>n;
    for ( int i = 2;i < pow(2,n+1);i++ )
    {
        cin>>a[i];
    }
    int ans = 0;
    for ( int i = pow(2,n+1);i!=0;i-=2 )
    {
        if ( a[i] > a[i+1] )
        {
            ans+=a[i]-a[i+1];
            a[i/2]+=a[i];
        }
        else
        {
            ans+=a[i+1]-a[i];
            a[(i+1)/2]+=a[i+1];
        }

    }
    cout<<ans<<endl;


    return 0;
}