算法笔记--基环树

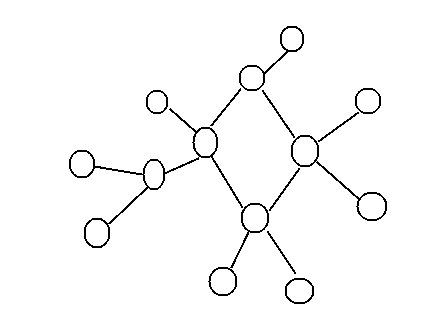
基环树：无向图，一个环，环上每个点都是树根

 

完备的扣环方法（可以扣二元环）：

void get_loop(int u) {
    vis[u] = ++vs;
    for (int i = head[u]; ~i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa[u]) continue;
        if(vis[v]) {
            if(vis[v] < vis[u]) continue;
            loop[++cnt] = v;
            for ( ;v != u; v = fa[v]) {
                loop[++cnt] = fa[v];
            }
        }
        else fa[v] = u, get_loop(v);
    }
}

例1：BZOJ 1791

思路：对于每个基环树，求出直径，然后加起来

基环树求直径方法，将基环树的环扣出来，求出以环上每个点为根节点的树的直径以及深度，然后在环上求边权前缀和，枚举j, 那么答案就是sum[j] - sum[i] + deep[j] + deep[i]，

用单调队列维护max{deep[i] - sum[i]}就行了，扣环的时候还可以用基环内向树建图扣，不过就不好求树的直径了。

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize(4)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define pi acos(-1.0)
#define LL long long
//#define mp make_pair
#define pb push_back
#define ls rt<<1, l, m
#define rs rt<<1|1, m+1, r
#define ULL unsigned LL
#define pll pair<LL, LL>
#define pii pair<int, int>
#define piii pair<pii, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define fopen freopen("in.txt", "r", stdin);freopen("out.txt", "w", stout);
//head

const int N = 1e6 + 5;
deque<int> q;
bool vs[N];
pii loop[N], fa[N];
int  cnt = 0, sz = 0, st, s, now, tot = 0, vis[N], head[N];
LL deep[N*2], sum[N*2], mx = 0;
struct edge {
    int to, w, nxt;
}edge[N*2];
void add_edge(int u, int v, int w) {
    edge[tot].to = v;
    edge[tot].w = w;
    edge[tot].nxt = head[u];
    head[u] = tot++;
}
void get_loop(int u) {
    vis[u] = ++sz;
    for (int i = head[u]; ~i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa[u].fi) continue;
        if(vis[v]) {
            if(vis[v] < vis[u]) continue;
            loop[++cnt].fi = v;
            loop[cnt].se = edge[i].w;
            for ( ;v != u; v = fa[v].fi) {
                loop[++cnt] = fa[v];
            }
        }
        else fa[v].fi = u, fa[v].se = edge[i].w, get_loop(v);
    }
}
void dfs(int o, int u, LL x) {
    if(x >= mx) {
        mx = x;
        s = u;
    }
    for (int i = head[u]; ~i ; i = edge[i].nxt) {
        if(edge[i].to != o && (!vs[edge[i].to] || edge[i].to == now)) {
            dfs(u, edge[i].to, x+edge[i].w);
        }
    }
}
LL f(int id) {
    return deep[id] - sum[id];
}
int main() {
    mem(head, -1);
    int n, u, v;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d %d", &u, &v);
        add_edge(i, u, v);
        add_edge(u, i, v);
    }
    LL ans = 0;
    sum[0] = deep[0] = 0;
    for (int i = 1; i <= n; i++) {
        if(!vis[i]) {
            cnt = 0;
            sz = 0;
            LL t = 0;
            get_loop(i);
            for (int j = 1; j <= cnt; j++) vs[loop[j].fi] = true;
            for (int j = 1; j <= cnt; j++) {
                mx = 0;
                now = -1;
                dfs(0, loop[j].fi, 0);
                deep[j] = mx;

                now = loop[j].fi;
                dfs(0, s, 0);
                t = max(t, mx);
            }
            for (int j = 1; j <= cnt; j++) deep[j+cnt] = deep[j];
            q.clear();
            for (int j = 1; j <= 2*cnt; j++) {
                if(j <= cnt)sum[j] = sum[j-1] + loop[j].se;
                else sum[j] = sum[j-1] + loop[j-cnt].se;
                if(!q.empty()) t = max(t, f(q.front()) + sum[j] + deep[j]);
                while(!q.empty() && f(q.back()) <= f(j)) q.pop_back();
                q.push_back(j);
                while(!q.empty() && q.front() <= j-cnt+1) q.pop_front();
            }
            ans += t;
        }
    }
    printf("%lld
", ans);
    return 0;
}

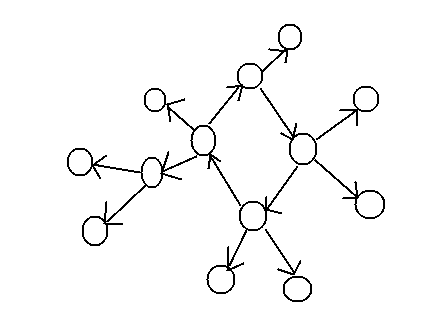
基环内向树：有向图，在基环树的基础上每个节点的出度为1

基环外向树：有向图，在基环树的基础上每个节点的入度为1