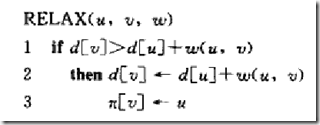经典计算机基础数据结构：图

1. 图的表示

大家都知道图有两种标准的表示方法：邻接表或者邻接矩阵。可是它们分别有什么样的好处呢？答案是：

• 邻接表适合稀疏图，而邻接矩阵时候稠密图；
• 要确定图中边(u,v)是否存在，只能在定点u的邻接表中搜索v，效率不高，而这时邻接矩阵就要方便的多了；

理论上知道了邻接表和邻接矩阵，如何用代码来实现呢？

#include <stdlib.h>
#include <queue>
using namespace std;

#define MAX_VERTEX_NUM 20
typedef enum _VisitedColor
{
    Black, White, Grey
}VisitedColor;
typedef struct _VertexNode
{
    int data;  //assume the data in the node is int typed;
    struct _ArcNode *firstArc;
    //below fields are for BFS or DFS, in real scenarios, we should not put them here, but it is just for demo the algorithm;
    VisitedColor visited; //for BFS and DFS
    struct _VertexNode * parent; //for BFS and DFS
    int distance; // the distance from source point to this node, for BFS and DFS 
}VertexNode;

typedef struct _ArcNode // This class represent a arc
{
    //VertexNode *from; //In Adjacency list, the ArcNode is to represent the arc, whose starting Node info is saved in the list, so we do not need define it here; 
    VertexNode *to;
    struct _ArcNode *next;
}ArcNode;

typedef struct _Graph
{
    int verNum, arcNum;
    VertexNode** vertices; 
}Graph;

再来一个C++的，它们是非常类似的，不过就是实现时可以show一下数据封装：

#include <iostream>
#include <list>
using namespace std;

class ArcNode;
class VertexNode
{
public:
    VertexNode(int _data)
    {
        data = _data;
    }
    void setFirstArc(ArcNode * arc)
    {
        firstArc = arc;
    }
private:
    int data;
    ArcNode *firstArc;
};

class ArcNode
{
public:
    ArcNode(VertexNode *_pointingto)
    {
        pointingto = _pointingto;
    }
private:
    VertexNode *pointingto;
};

class Graph
{
public:
    void AddOneArc(VertexNode *node, ArcNode *arc)
    {

    }
private:
    int arcNum, verNum;
    list<VertexNode *> vertices; 
};

应该来说邻接表是比较常用的，但邻接矩阵也是比较重要的，不过这里我就不贴代码了。

2. 广度优先搜索

这就不用多说了，breadth-first-search是最简单、最基本的图搜索算法之一，必须掌握的。在贴代码之前，先说一下注意点吧：1. 我们需要区分某个定点是否已经被发现了、是否其所有相邻节点都已经被发现了，在《算法导论》中使用颜色来区分这个状态，白色表示该节点没有被发现，灰色表示这个节点被发现了，而其相邻节点还没有完全被发现；而黑色表示这个节点极其相邻节点都已经被发现。 为什么要这么做呢？因为图的结构相对复杂，可能有多个边指向一个节点（也就是这个节点有多个路径可达，我们需要避免重复，因为重复就意味着路径可能是错的），可能有环（如果有环，而我们不区分是否已经被发现，就会进入死循环了）；2. 灰色节点是边缘节点，为了保证是按照BFS的顺序进行搜索，需要使用队列来管理灰色节点。

VertexNode * BFS(Graph *g, int pattern)
{
    int i = 0;
    for(;i<g->verNum;i++)
    {
        VertexNode *t = g->vertices[i];
        t->visited = White;
        t->parent = NULL;
        t->distance = -1;
    }
    VertexNode *s = g->vertices[0];
    s->visited = Grey;
    s->distance = 0;
    queue<VertexNode *> _queue;
    _queue.push(s);
    while(!_queue.empty())
    {
        s = _queue.front();
        if(s->data == pattern)
            return s;
        _queue.pop();
        ArcNode *arc = s->firstArc;
        for(;arc!=NULL;)
        {
            if(arc->to->visited == White)
            {
                if(arc->to->data == pattern)
                    return arc->to;
                arc->to->visited = Grey;//在这里将to的颜色改为grey才是对的，否则有可能被重复加入到队列中，
                arc->to->distance = s->distance + 1;
                _queue.push(arc->to);
            }
            arc = arc->next;
        }
        s->visited = Black;//for 结束后，也就是所有的孩子都已经被遍历过了，所以这时可以把其颜色设为black
    }
    return NULL;
}

3. 深度优先搜索

这就不用多说了，breadth-first-search是最简单、最基本的图搜索算法之一，必须掌握的。

VertexNode * DFS(Graph *g, int pattern)
{
    int i = 0;
    for(;i<g->verNum;i++)
    {
        VertexNode *t = g->vertices[i];
        t->visited = White;
        t->parent = NULL;
        t->distance = -1;
    }
    for(i = 0;i<g->verNum;i++)
    {
        VertexNode *t = g->vertices[i];
        if(t->visited == White)
        {
            t->distance=0;
            VertexNode *ret = DFS_visit(t, pattern);
            if(ret != NULL)
                return ret;
        }
    }


    return NULL;
}

VertexNode * DFS_visit(VertexNode *starting, int pattern)
{
    if(starting->data == pattern) return starting;
    starting->visited = Grey;
    ArcNode *arc = starting->firstArc;
    for(;arc!=NULL;)
    {
        if(arc->to->visited == White)
        {
            if(arc->to->data == pattern)
                return arc->to;
            arc->to->distance = starting->distance+1;
            DFS_visit(arc->to,pattern);
        }
        arc = arc->to->firstArc;
    }
    starting->visited = Black;
}

4. 拓扑排序

使用深度优先搜索，计算节点的发现开始和结束时间，然后按照结束时间排序，就是拓扑排序的结果。一个类似于拓扑排序的问题是，有若干需要执行的task，其中的某些task之间有依赖关系，求一个这些task的执行顺序。 输入的数据是若干task，然后每个task知道自己依赖于哪个task。如果使用典型的拓扑排序算法，要把task的依赖关系反转，使用另外一种数据结构temptask，temptask知道有哪些task依赖自己，也就是自己执行完后，哪些task可以开始执行。还有一个办法就是在原来数据结构的基础上，找到不依赖任何task的task，然后从其他task的依赖列表中将这个task删除，然后再重复这个过程，就可以得到task的一个执行顺序了。

5. 有向图的强连通分支

强连通分支的生成利用了强联通分支的重要性质：

6. 最小生成树

最小生成树是指在无向连通图中，一个边的子集，它连接了所有的顶点，并且其边的权值之和最小，这样的边形成的树称为最小生成树。最小生成树算法是用贪心算法来实现的，其算法核心是寻找生成树的安全边。根据定理，设割（S, V-S）是G的任意一个不妨害A的割，且边（u,v）是通过该割的一条轻边，则边(u,v)对集合A来说是安全的。证明过程看书吧。

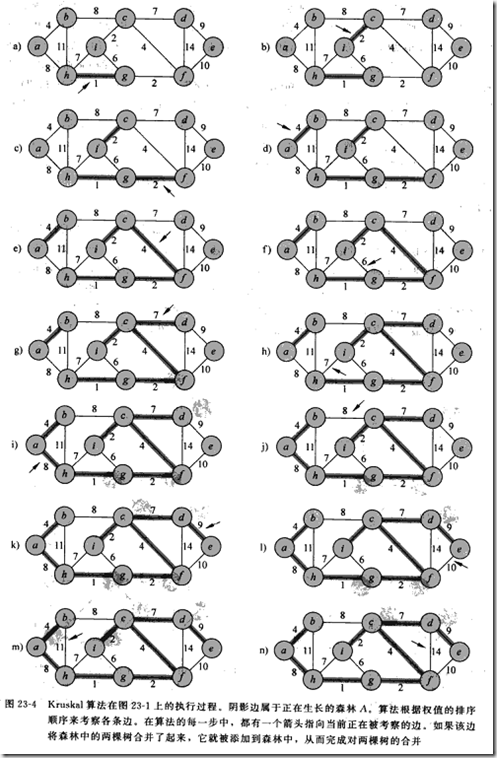
Kruskal算法：基于不相交集合的算法，从全局中选择边。步骤如下：

1. 使用各个顶点为节点构造森林；
2. 将所有的边按照权值排序；
3. 对排序后的边分别检查边的两个端点是否在同一个集合中，如果不在，就将这条边加到森林中，并将其所连接的两个集合合并；

下面是《算法导论》中给的图示：

Prim算法：从某个顶点出发选择边，步骤如下：

1. 将所有顶点放到一个最小优先级队列中；
2. 从这个队列中选择一个点u作为起点，计算这个点的边的权值，并把key(v)设置为边(u,v)的权值；
3. 从优先级队列中拿出key值最小的节点，放入最小生成树中；（由于其他节点尚未计算，所以此时拿出的节点就是跟u相连的节点中边权值最小的那个）
4. 不断重复2-3，使得最小优先级队列为空；

7. 单源最短路径

在这里我们只看Dijkstra算法，并且需要先了解松弛技术。

松弛技术是指对图中的每个顶点设置一个属性d[v]，用来描述从原点到v的最短路径上权值的上界。松弛一条边(u,v)的操作是这样的步骤，测试是否可以通过u对迄今为止找到的到v的最短路径进行改进， 如果可以，就更新d[v]和v的前驱，其伪代码如下：

Dijkstra算法的步骤：

1. 初始化单源；
2. 将所有定点加入到最小优先级队列中；
3. 从中取出第一个元素u（d[u]最小的那个，第一次调用时返回值是单源）；
4. 将这个元素u放入最短路径集合中，并对所有u的邻边进行松弛，更新邻居节点的d值；
5. 这时，回到第3步；